11.4: Muestreo Independiente — Comparación de Dos Varianzas Poblacionales o Desviaciones Estándar
- Page ID
- 151851
En ocasiones queremos probar si dos poblaciones tienen la misma extensión o variación, medida por varianza o desviación estándar. Esto puede ser una prueba por sí sola o una forma de verificar suposiciones al decidir entre dos modelos diferentes (por ejemplo: varianza agrupada\(t\) ‐prueba vs. varianza desigual\(t\) ‐prueba). Ahora exploraremos pruebas para detectar una diferencia en la varianza entre dos muestras independientes.
La\(\mathbf{F}\) distribución es una familia de distribuciones relacionadas con la Distribución Normal. Hay dos grados diferentes de libertad, generalmente representados como numerador (\(\mathrm{df}_{\text {num}}\)) y denominador (\(\mathrm{df}_{\text {den}}\)). Además, dado que la F representa datos cuadrados, la inferencia será sobre la varianza más que sobre la desviación estándar.
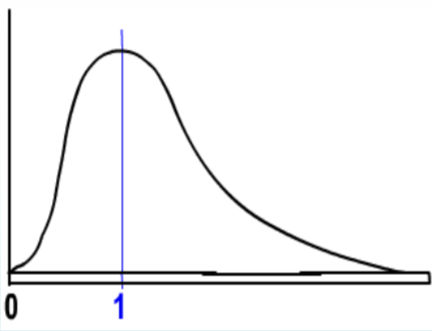
- Está sesgado positivamente
- No es negativo
- Hay 2 grados diferentes de libertad (\(\mathrm{df}_{\text {num}}\),\(\mathrm{df}_{\text {den}}\))
- Cuando cambian los grados de libertad, se crea una nueva distribución
- El valor esperado es 1.
\(\mathbf{F}\)prueba de igualdad de varianzas
Supongamos que quisiéramos probar la hipótesis nula de que dos desviaciones estándar de población son iguales,\(H_o: \sigma_{1}=\sigma_{2}\). Esto equivale a probar que las varianzas poblacionales son iguales:\(\sigma_{1}^{2}=\sigma_{2}^{2}\). Ahora vamos a escribir estos como una relación equivalente:\(H_o: \dfrac{\sigma_{1}^{2}}{\sigma_{2}^{2}}=1\) o\(H_o: \dfrac{\sigma_{2}^{2}}{\sigma_{2}^{1}}=1\).
Esta es la lógica detrás de la\(\mathbf{F}\) prueba; si dos varianzas poblacionales son iguales, entonces la relación de varianzas muestrales de cada población tendrá\(\mathbf{F}\) distribución. \(\mathbf{F}\)siempre será una prueba de cola superior en la práctica, por lo que la varianza mayor va en el numerador. Los estadísticos de las pruebas se resumen en la tabla.
| Hipótesis | Estadística de prueba |
|---|---|
| \ (\ begin {alineado} &H_ {o}:\ sigma_ {1}\ geq\ sigma_ {2}\\ &H_ {a}:\ sigma_ {1} <\ sigma_ {2} \ final {alineado}\) |
\(\mathbf{F}=\dfrac{s_{2}^{2}}{s_{1}^{2}}\)\(\alpha\)mesa de uso |
| \ (\ begin {alineado} &H_ {o}:\ sigma_ {1}\ leq\ sigma_ {2}\\ &H_ {a}:\ sigma_ {1} >\ sigma_ {2} \ final {alineado}\) |
\(\mathbf{F}=\dfrac{s_{1}^{2}}{s_{2}^{2}}\)\(\alpha\)mesa de uso |
| \ (\ begin {alineado} &H_ {o}:\ sigma_ {1} =\ sigma_ {2}\\ &H_ {a}:\ sigma_ {1}\ neq\ sigma_ {2} \ end {alineado}\) |
\(\mathbf{F}=\dfrac{\max \left(s_{1}^{2}, s_{2}^{2}\right)}{\min \left(s_{1}^{2}, s_{2}^{2}\right)}\)\(\alpha/2\)mesa de uso |
Ejemplo: Variación en existencias

Un corredor de bolsa de una firma de corretaje, informó que la tasa media de rendimiento de una muestra de 10 acciones de software (población 1) fue de 12.6 por ciento con una desviación estándar de 4.9 por ciento. La tasa media de rendimiento de una muestra de 8 existencias de servicios públicos (población 2) fue de 10.9, por ciento con una desviación estándar de 3.5 por ciento. En el nivel de significancia .05, ¿puede el corredor concluir que hay más variación en las acciones de software?
Solución
Diseño
Hipótesis de investigación:
\(H_o: \sigma_{1} \leq \sigma_{2}\)(Las existencias de software no tienen más variación)
\(H_a: \sigma_{1} > \sigma_{2}\)(Las existencias de software tienen más variación)
El modelo será\(\mathbf{F}\) prueba para varianzas y el estadístico de prueba de la tabla será\(\mathbf{F}=\dfrac{s_{1}^{2}}{s_{2}^{2}}\). Los grados de libertad para el numerador serán\(n_{1}-1=9\), y los grados de libertad para el denominador serán\(n_{2}-1=7\). La prueba se ejecutará a un nivel de significancia (\(\alpha\)) del 5%. Valor Crítico para\(\mathbf{F}\) con\(\mathrm{df}_{\text {num}}=9\) y\(\mathrm{df}_{\text {den}}=7\) es 3.68. Rechazar\(H_o\) si\(\mathbf{F}\) >3.68.
Datos/Resultados
\(\mathbf{F}=4.9^{2} / 3.5^{2}=1.96\), que es menor que el valor crítico, por lo que No Rechazar\(H_o\).
Conclusión
No hay pruebas suficientes para reclamar más variación en el stock de software.
Ejemplo: Prueba de suposiciones del modelo
Al comparar dos medias de muestras independientes, puede elegir entre la varianza agrupada más poderosa\(t\) ‐test (la suposición es\(\sigma_{1}^{2}=\sigma_{2}^{2}\)) o la varianza desigual más débil\(t\) ‐test (la suposición es\(\sigma_{1}^{2} \neq \sigma_{2}^{2}\). Ahora podemos diseñar una prueba de hipótesis que nos ayude a elegir el modelo adecuado. Revisemos el ejemplo de comparar el MPG para autos compactos de importación y nacionales. Considera este ejemplo una “prueba antes de la prueba principal” para ayudar a elegir el modelo correcto para comparar medias.
Solución
Diseño
Hipótesis de investigación:
\(H_o: \sigma_{1} = \sigma_{2}\)(elija la\(t\) prueba de varianza agrupada para comparar medias)
\(H_a: \sigma_{1} \neq \sigma_{2}\)(elija la\(t\) prueba de varianza desigual para comparar medias)
El modelo será\(\mathbf{F}\) prueba para varianzas, y el estadístico de prueba de la tabla será\(\mathbf{F}=\dfrac{s_{1}^{2}}{s_{2}^{2}}\) (\(s_1\)es más grande). Los grados de libertad para el numerador serán\(n_{1}-1=11\) y los grados de libertad para denominador serán\(n_2‐1=14\). La prueba se ejecutará a un nivel de significancia (\(\alpha\)) del 10%, pero se utilizará la tabla\(\alpha\) =.05 para una prueba de dos colas. Valor Crítico para\(\mathbf{F}\) con\(\mathrm{df}_{\text {num}}=11\) y\(\mathrm{df}_{\text {den}}=14\) es 2.57. Rechazar\(H_o\) si\(\mathbf{F}\) >2.57.
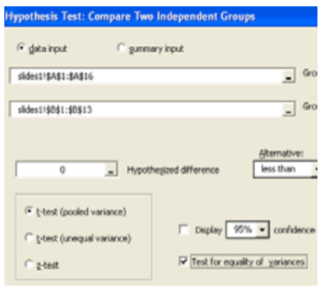
También realizaremos esta prueba de la manera\(p\) ‐valor en Megasat.
Datos/Resultados
\(\mathbf{F}=14.894 / 4.654=3.20\), que es más que valor crítico; Rechazar\(H_o\).
También\(p\) ‐valor = 0.0438 < 0.10, lo que también hace que el resultado sea significativo.
Conclusión
No asuma varianzas iguales y ejecute la prueba de varianza desigual\(t\) ‐test para comparar medias poblacionales
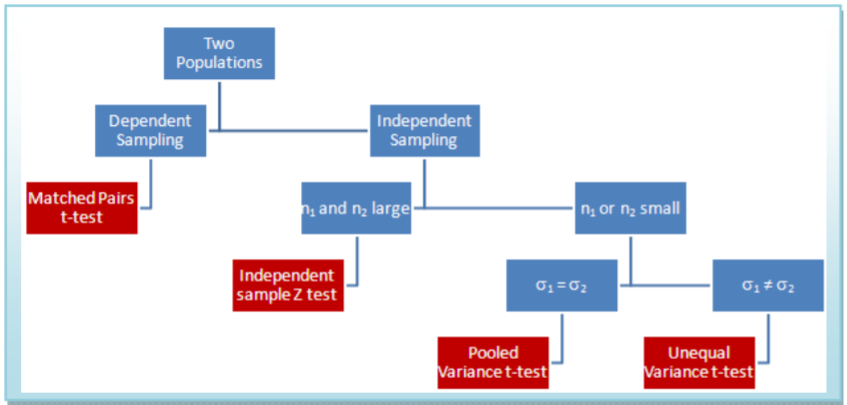
En Resumen
Este diagrama de flujo resume cuál de los cuatro modelos elegir al comparar dos medias de población. Además, puede utilizar el\(\mathbf{F}\) ‐test para la igualdad de varianzas para tomar la decisión entre la varianza de pool\(t\) ‐test y la varianza desigual\(t\) ‐test.