4.1: Introducción a los datos bivariados
- Page ID
- 152436
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Definir “datos bivariados”
- Definir “diagrama de dispersión”
- Distinguir entre una relación lineal y una no lineal
- Identificar asociaciones positivas y negativas a partir de un diagrama de dispersión
Las medidas de tendencia central, variabilidad y dispersión resumen una sola variable proporcionando información importante sobre su distribución. A menudo, se recolecta más de una variable en cada individuo. Por ejemplo, en grandes estudios de salud de poblaciones es común obtener variables como edad, sexo, talla, peso, presión arterial y colesterol total en cada individuo. Los estudios económicos pueden interesarle, entre otras cosas, los ingresos personales y los años de educación. Como tercer ejemplo, la mayoría de los comités de admisión universitarios piden el promedio de calificaciones de la escuela secundaria y los puntajes de las pruebas de admisión estandarizadas de un solicitante (por ejemplo, SAT). En este capítulo consideramos los datos bivariados, que por ahora consisten en dos variables cuantitativas para cada individuo. Nuestro primer interés es resumir dichos datos de una manera análoga a resumir datos univariados (variable única).
A modo de ilustración, consideremos algo con lo que todos conocemos: la edad. Empecemos por preguntar si las personas tienden a casarse con otras personas de aproximadamente la misma edad. Nuestra experiencia nos dice “sí”, pero ¿qué tan buena es la correspondencia? Una forma de abordar la pregunta es mirar pares de edades para una muestra de parejas casadas. La\(\PageIndex{1}\) siguiente tabla muestra las edades de las parejas\(10\) casadas. Al cruzar las columnas vemos que, sí, los esposos y las esposas tienden a ser de aproximadamente la misma edad, con los hombres que tienden a ser un poco mayores que sus esposas. Esto no es una gran sorpresa, pero al menos los datos confirman nuestras experiencias, lo que no siempre es así.
| Marido | 36 | 72 | 37 | 36 | 51 | 50 | 47 | 50 | 37 | 41 |
|---|---|---|---|---|---|---|---|---|---|---|
| Esposa | 35 | 67 | 33 | 35 | 50 | 46 | 47 | 42 | 36 | 41 |
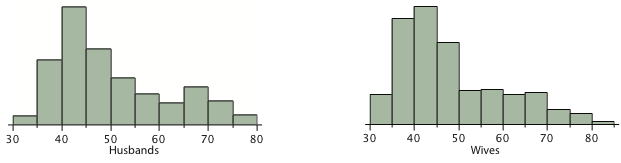
Los pares de edades en Table\(\PageIndex{1}\) son de un conjunto de datos que consiste en\(282\) pares de edades conyugales, demasiados para darle sentido a partir de una tabla. Lo que necesitamos es una manera de resumir los\(282\) pares de edades. Sabemos que cada variable puede ser resumida por un histograma (ver Figura\(\PageIndex{1}\)) y por una media y desviación estándar (Ver Tabla\(\PageIndex{2}\)).
| Media | Desviación estándar |
|
|---|---|---|
| Maridos | 49 | 11 |
| Esposas | 47 | 11 |
Cada distribución es bastante sesgada con una larga cola derecha. De Table\(\PageIndex{1}\) vemos que no todos los esposos son mayores que sus esposas y es importante ver que este hecho se pierde cuando separamos las variables. Es decir, a pesar de que proporcionamos estadísticas resumidas sobre cada variable, el emparejamiento dentro de la pareja se pierde al separar las variables. No podemos decir, por ejemplo, con base únicamente en los medios qué porcentaje de parejas tiene esposos más jóvenes que esposas. Tenemos que contar entre pares para averiguarlo. Solo manteniendo el emparejamiento se pueden encontrar respuestas significativas sobre las parejas per se. Otro ejemplo de información no disponible de las descripciones separadas de las edades de esposos y esposas es la edad media de los esposos con esposas de cierta edad. Por ejemplo, ¿cuál es la edad promedio de los esposos con esposas\(45\) de un año? Por último, desconocemos la relación entre la edad del marido y la edad de la esposa.
Podemos aprender mucho más mostrando los datos bivariados en una forma gráfica que mantenga el emparejamiento. La figura\(\PageIndex{2}\) muestra un diagrama de dispersión de las edades emparejadas. El\(x\) eje representa la edad del marido y el\(y\) eje la edad de la esposa.
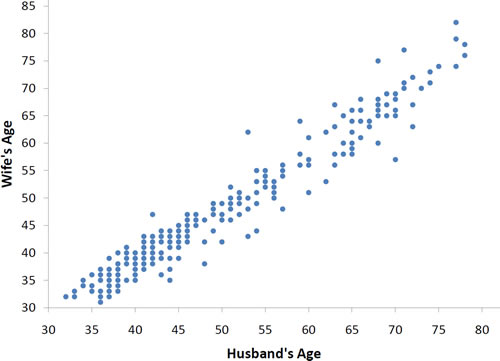
Hay dos características importantes de los datos revelados por la Figura\(\PageIndex{2}\). Primero, es claro que existe una fuerte relación entre la edad del esposo y la edad de la esposa: cuanto mayor es el esposo, mayor es la esposa. Cuando una variable (\(Y\)) aumenta con la segunda variable (\(X\)), decimos eso\(X\) y\(Y\) tenemos una asociación positiva. Por el contrario, cuando\(Y\) disminuye a medida que\(X\) aumenta, decimos que tienen una asociación negativa.
Segundo, los puntos se agrupan a lo largo de una línea recta. Cuando esto ocurre, la relación se llama relación lineal.
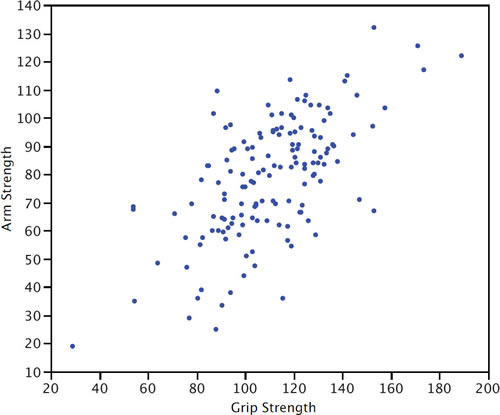
La figura\(\PageIndex{3}\) muestra un diagrama de dispersión de Fuerza de Brazo y Fuerza de Agarre de\(149\) individuos que trabajan en trabajos físicamente exigentes, incluyendo electricistas, trabajadores de construcción y mantenimiento, y mecánicos de automóviles. No es sorprendente que cuanto más fuerte tenga el agarre de alguien, más fuerte tiende a ser su brazo. Por lo tanto, existe una asociación positiva entre estas variables. Aunque los puntos se agrupan a lo largo de una línea, no se agrupan tan estrechamente como lo están para el diagrama de dispersión de la edad conyugal.
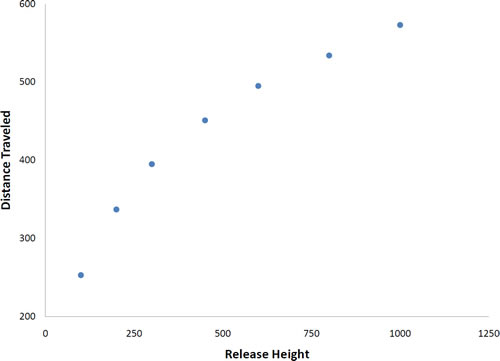
No todas las gráficas de dispersión muestran relaciones lineales. La figura\(\PageIndex{4}\) muestra los resultados de un experimento realizado por Galileo sobre el movimiento del proyectil. En el experimento, Galileo rodó bolas por una pendiente y midió hasta dónde viajaban en función de la altura de liberación. Es claro a partir de Figura\(\PageIndex{4}\) que la relación entre “Altura de Liberación” y “Distancia recorrida” no se describe bien por una línea recta: Si dibujaste una línea que conecta el punto más bajo y el punto más alto, todos los puntos restantes estarían por encima de la línea. Los datos se ajustan mejor por una parábola.
D. Dickey y T. Arnold describen el estudio incluyendo una película
Los gráficos de dispersión que muestran relaciones lineales entre variables pueden diferir de varias maneras, incluida la pendiente de la línea sobre la que se agrupan y la fuerza con la que se agrupan los puntos alrededor de la línea. Una medida estadística de la fuerza de la relación entre dos variables cuantitativas que toma en cuenta estos factores es el tema de la sección “Valores de correlación de Pearson”.
Colaborador
- Template:ContribHeblLane
- Rudy Guerra and David M. Lane


