11.4: Pruebas de una y Dos Colas
- Page ID
- 152385
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Definir errores de Tipo I y Tipo II
- Interpretar diferencias significativas y no significativas
- Explicar por qué no se debe aceptar la hipótesis nula cuando el efecto no es significativo
En el caso de estudio de James Bond, el señor Bond recibió\(16\) juicios en los que juzgó si un martini había sido sacudido o agitado. Estaba en lo cierto sobre\(13\) los juicios. A partir de la distribución binomial, sabemos que la probabilidad de ser correctos\(13\) o más veces fuera de\(16\) si uno solo está adivinando lo es\(0.0106\). La figura\(\PageIndex{1}\) muestra una gráfica de la distribución binomial. Las barras rojas muestran los valores mayores o iguales a\(13\). Como puede ver en la figura, se calculan las probabilidades para la cola superior de la distribución. Una probabilidad calculada en una sola cola de la distribución se denomina “probabilidad de una cola”.
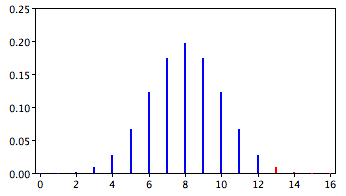
Calculadora binomial
Se puede hacer una pregunta ligeramente diferente a los datos: “¿Cuál es la probabilidad de obtener un resultado tan extremo o más extremo que el observado?” Dado que la expectativa de oportunidad es\(8/16\), un resultado de\(3/16\) es igual de extremo como\(13/16\). Así, para calcular esta probabilidad, consideraríamos ambas colas de la distribución. Dado que la distribución binomial es simétrica cuando\(\pi =0.5\), esta probabilidad es exactamente el doble de la probabilidad de\(0.0106\) calculada previamente. Por lo tanto,\(p = 0.0212\). Una probabilidad calculada en ambas colas de una distribución se denomina “probabilidad de dos colas” (ver Figura\(\PageIndex{2}\)).
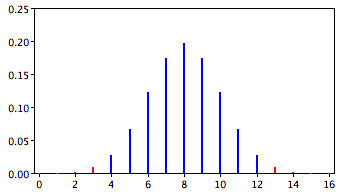
¿Se debe utilizar la probabilidad de una cola o la de dos colas para evaluar el desempeño del señor Bond? Eso depende de la forma en que se plantee la pregunta. Si nos estamos preguntando si el señor Bond puede notar la diferencia entre martinis agitados o agitados, entonces concluiríamos que podría si se desempeñaba mucho mejor que el azar o mucho peor que el azar. Si se desempeñó mucho peor que el azar, concluiríamos que puede notar la diferencia, pero no sabe cuál es cuál. Por lo tanto, como vamos a rechazar la hipótesis nula si al señor Bond le va muy bien o muy mal, usaremos una probabilidad de dos colas.
Por otro lado, si nuestra pregunta es si el señor Bond es mejor que el azar para determinar si un martini es sacudido o revuelto, usaríamos una probabilidad de una cola. ¿Cuál sería la probabilidad de una cola si el señor Bond tuviera razón solo en\(3\) los\(16\) juicios? Dado que la probabilidad de una cola es la probabilidad de la cola derecha, sería la probabilidad de salir\(3\) o más correcta de\(16\). Esta es una probabilidad muy alta y la hipótesis nula no sería rechazada.
La hipótesis nula para la prueba de dos colas es\(\pi =0.5\). Por el contrario, la hipótesis nula para la prueba de una cola es\(\pi \leq 0.5\). En consecuencia, rechazamos la hipótesis de dos colas si la proporción muestral se desvía mucho\(0.5\) de cualquier dirección. La hipótesis de una cola es rechazada sólo si la proporción muestral es mucho mayor que\(0.5\). La hipótesis alternativa en la prueba de dos colas es\(\pi \neq 0.5\). En la prueba de una cola es\(\pi > 0.5\).
Siempre debes decidir si vas a usar una probabilidad de una cola o una de dos colas antes de mirar los datos. Las pruebas estadísticas que calculan probabilidades de una cola se denominan pruebas de una cola; las que calculan probabilidades de dos colas se denominan pruebas de dos colas. Las pruebas de dos colas son mucho más comunes que las pruebas de una cola en la investigación científica porque generalmente vale la pena señalar un resultado que significa que algo distinto al azar está operando. Las pruebas de una cola son apropiadas cuando no es importante distinguir entre ningún efecto y un efecto en la dirección inesperada. Por ejemplo, considere un experimento diseñado para probar la eficacia de un tratamiento para el resfriado común. Al investigador sólo le interesaría si el tratamiento era mejor que un control placebo. No valdría la pena distinguir entre el caso en el que el tratamiento fue peor que un placebo y el caso en el que fue el mismo porque en ambos casos el medicamento sería inservible.
Algunos han argumentado que una prueba de una cola se justifica siempre que el investigador predice la dirección de un efecto. El problema con este argumento es que si el efecto sale fuertemente en la dirección no predicha, el investigador no está justificado en concluir que el efecto no es cero. Dado que esto no es realista, las pruebas de una cola generalmente se ven con escepticismo si se justifican solo sobre esta base.


