12.1: Prueba de una Media Única
- Page ID
- 152003
Objetivos de aprendizaje
- Calcular la probabilidad de que una media de muestra sea al menos tan alta como un valor especificado cuando\(\sigma\) se conoce
- Calcular una probabilidad de dos colas
- Calcular la probabilidad de que una media de muestra sea al menos tan alta como un valor especificado cuando\(\sigma\) se estima
- Indicar los supuestos requeridos para el ítem\(3\) anterior
En esta sección se muestra cómo probar la hipótesis nula de que la media poblacional es igual a algún valor hipotético. Por ejemplo, supongamos que un experimentador quería saber si las personas están influenciadas por un mensaje subliminal y realizó el siguiente experimento. Cada uno de los nueve temas se presenta con una serie de\(100\) pares de imágenes. A medida que se presenta un par de imágenes, se presenta un mensaje subliminal sugiriendo la imagen que el sujeto debe elegir. La cuestión es si el número medio (poblacional) de veces que se elige la imagen sugerida es igual a\(50\). Es decir, la hipótesis nula es que la media poblacional (\(\mu\)) es\(50\). Los datos (hipotéticos) se muestran en la Tabla\(\PageIndex{1}\). Los datos en la Tabla\(\PageIndex{1}\) tienen una media muestral (\(M\)) de\(51\). Así, la media de la muestra difiere de la media de la población hipotética por\(1\).
| Frecuencia |
|---|
| 45 |
| 48 |
| 49 |
| 49 |
| 51 |
| 52 |
| 53 |
| 55 |
| 57 |
La prueba de significancia consiste en computar la probabilidad de que una media\(\mu\) muestral difiera de una (la diferencia entre la media poblacional hipotética y la media muestral) o más. El primer paso es determinar la distribución muestral de la media. Como se muestra en una sección anterior, la media y desviación estándar de la distribución muestral de la media son
\[μ_M = μ\]
y
\[\sigma_M = \dfrac{\sigma}{\sqrt{N}}\]
respectivamente. Eso es claro\(\mu _M=50\). Para calcular la desviación estándar de la distribución muestral de la media, tenemos que conocer la desviación estándar poblacional (\(\sigma\)).
El ejemplo actual se construyó para ser uno de los pocos casos en los que se conoce la desviación estándar. En la práctica, es muy poco probable que conozcas\(\sigma\) y por lo tanto usarías\(s\), la estimación muestral de\(\sigma\). No obstante, es instructivo ver cómo se calcula la probabilidad si\(\sigma\) se conoce antes de proceder para ver cómo se calcula cuando\(\sigma\) se estima.
Para el ejemplo actual, si la hipótesis nula es verdadera, entonces con base en la distribución binomial, se puede calcular que la varianza del número correcto es
\[\sigma ^2 = N\pi (1-\pi ) = 100(0.5)(1-0.5) = 25\]
Por lo tanto,\(\sigma =5\). Para una\(\sigma \) de\(5\) y una\(N\) de\(9\), la desviación estándar de la distribución muestral de la media es\(5/3 = 1.667\). Recordemos que la desviación estándar de una distribución de muestreo se denomina error estándar.
Para recapitular, se desea conocer la probabilidad de obtener una media muestral de\(51\) o más cuando la distribución muestral de la media tiene una media de\(50\) y una desviación estándar de\(1.667\). Para calcular esta probabilidad, haremos la suposición de que la distribución muestral de la media se distribuye normalmente. Luego podemos usar la calculadora de distribución normal como se muestra en la Figura\(\PageIndex{1}\).
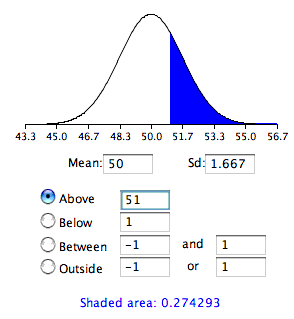
Observe que la media se establece en\(50\), la desviación estándar a\(1.667\), y\(51\) se solicita el área anterior y se muestra que es\(0.274\).
Por lo tanto, la probabilidad de obtener una media muestral de\(51\) o mayor es\(0.274\). Dado que una media\(51\) o superior no es improbable bajo el supuesto de que el mensaje subliminal no tiene efecto, el efecto no es significativo y no se rechaza la hipótesis nula.
La prueba realizada anteriormente fue una prueba de una cola porque computó la probabilidad de que una media muestral sea uno o más puntos mayor que la media hipotética de\(50\) y el área calculada fue el área anterior\(51\). Para probar la hipótesis de dos colas, calcularía la probabilidad de que una media de la muestra difiera en una o más en cualquier dirección de la media hipotética de\(50\). Lo harías calculando la probabilidad de que una media sea menor o igual\(49\) o mayor que o igual a\(51\).
Los resultados de la calculadora de distribución normal se muestran en la Figura\(\PageIndex{2}\).
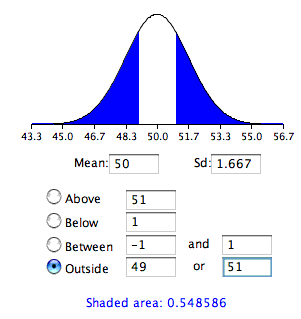
Como puede ver, la probabilidad es\(0.548\) que, como se esperaba, es el doble de probabilidad que\(0.274\) se muestra en la Figura\(\PageIndex{1}\).
Antes de que las calculadoras normales como la ilustrada anteriormente estuvieran ampliamente disponibles, los cálculos de probabilidad se realizaron con base en la distribución normal estándar. Esto se hizo mediante computación\(Z\) basada en la fórmula
\[Z=\frac{M-\mu }{\sigma _M}\]
donde\(Z\) es el valor en la distribución normal estándar,\(M\) es la media muestral,\(\mu\) es el valor hipotético de la media, y\(\sigma _M\) es el error estándar de la media. Para este ejemplo,\(Z = (51-50)/1.667 = 0.60\). Utilice la calculadora normal, con una media de\(0\) y una desviación estándar de\(1\), como se muestra a continuación.
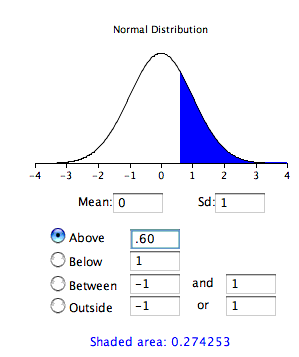
Observe que la probabilidad (el área sombreada) es la misma que la calculada previamente (para la prueba de una cola).
Como se señaló, en el análisis de datos del mundo real es muy raro que conozcas\(\sigma\) y desees estimar\(\mu\). Normalmente no\(\sigma\) se conoce y se estima en una muestra por\(s\), y\(\sigma _M\) se estima por\(s_M\).
Ejemplo\(\PageIndex{1}\): adhd treatment
C onsider los datos en el estudio de caso “Tratamiento del TDAH”. Estos datos consisten en las puntuaciones de\(24\) niños con TDAH en una tarea de retraso de gratificación (DOG). Cada niño fue probado bajo cuatro niveles de dosificación. En el cuadro se\(\PageIndex{2}\) muestran los datos para el placebo (\(0\)mg) y el nivel de dosificación más alto (\(0.6\)mg) de metilfenidato. De particular interés aquí es la columna etiquetada “Diff” que muestra la diferencia en el rendimiento entre la condición\(0.6\) mg (\(D60\)) y la\(0\)\(D0\)) conditions. These difference scores are positive for children who performed better in the \(0.6\) mg (mg) que en la condición control y negativa para aquellas quienes obtuvieron mejores puntajes en la condición de control. Si el metilfenidato tiene un efecto positivo, entonces la puntuación de diferencia media en la población será positiva. La hipótesis nula es que el puntaje de diferencia media en la población es\(0\).
Tabla\(\PageIndex{2}\): Puntajes DOG en función de la dosis
| D0 | D60 | Diff |
|---|---|---|
| 57 | 62 | 5 |
| 27 | 49 | 22 |
| 32 | 30 | -2 |
| 31 | 34 | 3 |
| 34 | 38 | 4 |
| 38 | 36 | -2 |
| 71 | 77 | 6 |
| 33 | 51 | 18 |
| 34 | 45 | 11 |
| 53 | 42 | -11 |
| 36 | 43 | 7 |
| 42 | 57 | 15 |
| 26 | 36 | 10 |
| 52 | 58 | 6 |
| 36 | 35 | -1 |
| 55 | 60 | 5 |
| 36 | 33 | -3 |
| 42 | 49 | 7 |
| 36 | 33 | -3 |
| 54 | 59 | 5 |
| 34 | 35 | 1 |
| 29 | 37 | 8 |
| 33 | 45 | 12 |
| 33 | 29 | -4 |
Solución
Para probar esta hipótesis nula, calculamos\(t\) using a special case of the following formula:
\[t=\frac{\text{statistic-hypothesized value}}{\text{estimated standard error of the statistic}}\]
El caso especial de esta fórmula aplicable a la prueba de una sola media es
\[t=\frac{M-\mu }{s_M}\]
donde\(t\) is the value we compute for the significance test, \(M\) is the sample mean, \(\mu\) está el valor hipotético de la media poblacional, y\(s_M\) es el error estándar estimado de la media. Observe la similitud de esta fórmula con la fórmula para Z.
En el ejemplo anterior, asumimos que los puntajes se distribuían normalmente. En este caso, es la población de puntuaciones de diferencia la que suponemos que se distribuye normalmente.
La media (\(M\)) of the \(N = 24\) difference scores is \(4.958\), the hypothesized value of \(\mu\)es\(0\), and the standard deviation (\(s\)) is \(7.538\). The estimate of the standard error of the mean is computed as:
\[s_M=\frac{s}{\sqrt{N}}=\frac{7.5382}{\sqrt{24}}=1.54\]
Por lo tanto,
\[t =\frac{4.96}{1.54} = 3.22\]
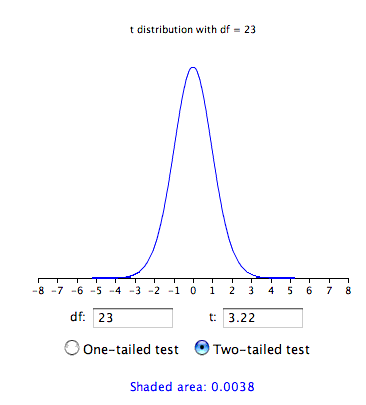
El valor de probabilidad para la calculadora de distribución\(t\) depends on the degrees of freedom. The number of degrees of freedom is equal to \(N - 1 = 23\). As shown below, the t encuentra que la probabilidad de\(t\) less than \(-3.22\) or greater than \(3.22\) is only \(0.0038\). Therefore, if the drug had no effect, the probability of finding a difference between means as large or larger (in either direction) than the difference found is very low. Therefore the null hypothesis that the population mean difference score is zero can be rejected. The conclusion is that the population mean for the drug condition is higher than the population mean for the placebo condition.
Revisión de suposiciones
- Cada valor se muestrea independientemente uno del otro valor.
- Los valores se muestrean a partir de una distribución normal.


