12.3: Diferencia entre dos medias
- Page ID
- 152010
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Exponer los supuestos para probar la diferencia entre dos medias
- Estimar la varianza poblacional asumiendo homogeneidad de varianza
- Calcular el error estándar de la diferencia entre medias
- Calcular\(t\) y\(p\) para la diferencia entre medias
- Dar formato a los datos para análisis por computadora
Es mucho más común que un investigador esté interesado en la diferencia entre medias que en los valores específicos de los propios medios. Esta sección cubre cómo probar las diferencias entre medias de dos grupos separados de sujetos. Una sección posterior describe cómo probar las diferencias entre las medias de dos condiciones en diseños donde solo se usa un grupo de sujetos y cada sujeto se prueba en cada condición.
Tomamos como ejemplo los datos del estudio de caso “Animal Research”. En este experimento, los estudiantes calificaron (en una escala\(7\) de puntos) si pensaban que la investigación animal es incorrecta. Los tamaños de muestra, medias y varianzas se muestran por separado para machos y hembras en la Tabla\(\PageIndex{1}\).
| Grupo | n | Media | Varianza |
|---|---|---|---|
| Hembras | 17 | 5.353 | 2.743 |
| Machos | 17 | 3.882 | 2.985 |
Como puede ver, las hembras calificaron la investigación animal como más equivocada que los machos. Esta diferencia muestral entre la media femenina de\(5.35\) y la media masculina de\(3.88\) es\(1.47\). Sin embargo, la diferencia de género en esta muestra en particular no es muy importante. Lo importante es si hay una diferencia en las medias poblacionales.
Para probar si existe una diferencia entre las medias poblacionales, vamos a hacer tres suposiciones:
- Las dos poblaciones tienen la misma varianza. Esta suposición se llama la suposición de homogeneidad de varianza.
- Las poblaciones se distribuyen normalmente.
- Cada valor se muestrea independientemente uno del otro valor. Esta suposición requiere que cada sujeto proporcione un solo valor. Si un sujeto proporciona dos puntajes, entonces los puntajes no son independientes. El análisis de datos con dos puntuaciones por materia se muestra en la sección sobre la prueba t correlacionada más adelante en este capítulo.
Las consecuencias de violar los dos primeros supuestos se investigan en la simulación en la siguiente sección. Por ahora, basta con decir que las violaciones pequeñas a moderadas de los supuestos\(1\) y no\(2\) hacen mucha diferencia. Es importante no violar la suposición\(3\).
Vimos la siguiente fórmula general para las pruebas de significancia en la sección sobre la prueba de una sola media:
\[t=\frac{\text{statistic-hypothesized value}}{\text{estimated standard error of the statistic}}\]
En este caso, nuestra estadística es la diferencia entre medias muestrales y nuestro valor hipotético es\(0\). El valor hipotético es la hipótesis nula de que es la diferencia entre medias poblacionales\(0\).
Seguimos utilizando los datos del estudio de caso “Animal Research” y calcularemos una prueba de significancia sobre la diferencia entre la puntuación media de las hembras y la puntuación media de los machos. Para este cálculo, realizaremos los tres supuestos especificados anteriormente.
El primer paso es calcular la estadística, que es simplemente la diferencia entre medias.
\[M_1 - M_2 = 5.3529 - 3.8824 = 1.4705\]
Dado que el valor hipotético es\(0\), no necesitamos restarlo de la estadística.
El siguiente paso es calcular la estimación del error estándar de la estadística. En este caso, el estadístico es la diferencia entre medias, por lo que el error estándar estimado del estadístico es (\(S_{M_1 - M_2}\)). Recordemos de la sección relevante del capítulo sobre distribuciones de muestreo que la fórmula para el error estándar de la diferencia entre medias es:
\[\sigma _{M_1 - M_2}=\sqrt{\frac{\sigma _{1}^{2}}{n_1}+\frac{\sigma _{2}^{2}}{n_2}}=\sqrt{\frac{\sigma ^2}{n}+\frac{\sigma ^2}{n}}=\sqrt{\frac{2\sigma ^2}{n}}\]
Para estimar esta cantidad, estimamos\(\sigma ^2\) y utilizamos esa estimación en lugar de\(\sigma ^2\). Dado que estamos asumiendo que las dos varianzas poblacionales son las mismas, estimamos esta varianza promediando nuestras dos varianzas muestrales. Así, nuestra estimación de varianza se calcula utilizando la siguiente fórmula:
\[MSE=\frac{s_{1}^{2}+s_{2}^{2}}{2}\]
donde\(MSE\) esta nuestra estimacion de\(\sigma ^2\). En este ejemplo,
\[MSE = \frac{2.743 + 2.985}{2} = 2.864\]
Dado que\(n\) (el número de puntajes en cada grupo) es\(17\),
\[S_{M_1-M_2}=\sqrt{\frac{2MSE}{n}}=\sqrt{\frac{(2)(2.864)}{17}}=0.5805\]
El siguiente paso es calcular\(t\) mediante la conexión de estos valores en la fórmula:
\[t = \frac{1.4705}{0.5805} = 2.533\]
Finalmente, calculamos la probabilidad de obtener un tamaño\(t\) tan grande o mayor que\(2.533\) o como pequeño o menor que\(-2.533\). Para ello, necesitamos conocer los grados de libertad. Los grados de libertad es el número de estimaciones independientes de varianza en las que\(MSE\) se basa. Esto es igual a\((n_1 - 1) + (n_2 - 1)\), donde\(n_1\) está el tamaño de muestra del primer grupo y\(n_2\) es el tamaño de muestra del segundo grupo. Para este ejemplo,\(n_1 = n_2 = 17\). Cuando\(n_1 = n_2\), es convencional utilizar ""\(n\) "para referirse al tamaño muestral de cada grupo. Por lo tanto, los grados de libertad lo son\(16 + 16 = 32\).
Una vez que tenemos los grados de libertad, podemos usar la calculadora de distribución t para encontrar la probabilidad. La figura\(\PageIndex{1}\) muestra que el valor de probabilidad para una prueba de dos colas es\(0.0164\). La prueba de dos colas se utiliza cuando la hipótesis nula puede ser rechazada independientemente de la dirección del efecto. Como se muestra en la Figura\(\PageIndex{1}\), es la probabilidad de a\(t < -2.533\) o a\(t > 2.533\).
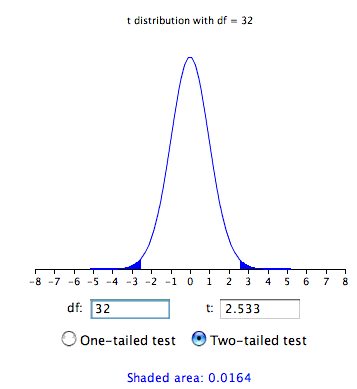
Los resultados de una prueba de una cola se muestran en la Figura\(\PageIndex{2}\). Como puede ver, el valor de probabilidad de\(0.0082\) es la mitad del valor para la prueba de dos colas.
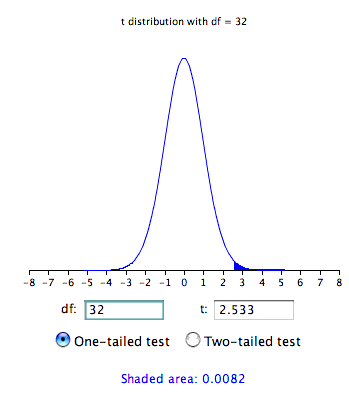
Formateo de Datos para Análisis por Computadora
La mayoría de los programas informáticos que calculan\(t\) pruebas requieren que tus datos estén en una forma específica. Considera los datos en la Tabla\(\PageIndex{2}\).
| Grupo 1 | Grupo 2 |
|---|---|
| 3 | 2 |
| 4 | 6 |
| 5 | 8 |
Aquí hay dos grupos, cada uno con tres observaciones. Para formatear estos datos para un programa de computadora, normalmente hay que usar dos variables: la primera especifica el grupo en el que se encuentra el sujeto y la segunda es la propia puntuación. La versión reformateada de los datos en la Tabla\(\PageIndex{2}\) se muestra en la Tabla\(\PageIndex{3}\).
| G | Y |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 2 | 2 |
| 2 | 6 |
| 2 | 8 |
Para usar Analysis Lab para hacer los cálculos, copiaría los datos y luego
- Haga clic en el botón “Ingresar/Editar datos”. (Es posible que se le avise que por razones de seguridad debe usar el método abreviado de teclado para pegar datos).
- Pega tus datos.
- Haga clic en “Aceptar datos”.
- Establezca la variable dependiente en\(Y\).
- Establezca la variable de agrupación en\(G\).
- Haga clic en el botón "\(t\)-prueba/intervalo de confianza”.
El\(t\) valor es\(-0.718\), el\(df = 4\), y\(p = 0.512\).
Cálculos para Tamaños de Muestra Desiguales (opcional)
Los cálculos son algo más complicados cuando los tamaños de muestra no son iguales. Una consideración es que\(MSE\), la estimación de varianza, cuenta el grupo con el tamaño de muestra más grande que el grupo con el tamaño de muestra más pequeño. Computacionalmente, esto se hace calculando la suma de cuadrados error (\(SSE\)) de la siguiente manera:
\[SSE=\sum (X-M_1)^2+\sum (X-M_2)^2\]
donde\(M_1\) es la media para grupo\(1\) y\(M_2\) es la media para grupo\(2\). Considera el siguiente pequeño ejemplo:
| Grupo 1 | Grupo 2 |
|---|---|
| 3 | 2 |
| 4 | 4 |
| 5 |
\[M_1 = 4 \; \text{and}\; M_2 = 3\]
\[SSE = (3-4)^2 + (4-4)^2 + (5-4)^2 + (2-3)^2 + (4-3)^2 = 4\]
Entonces,\(MSE\) se computa por:
\[MSE = \frac{SSE}{df}\]
donde los grados de libertad (\(df\)) se computan como antes:
\[df = (n_1 - 1) + (n_2 - 1) = (3 - 1) + (2 - 1) = 3\]
\[MSE = \frac{SSE}{df}=\frac{4}{3}=1.333\]
La fórmula
\[S_{M_1-M_2}=\sqrt{\frac{2MSE}{n}}\]
se sustituye por
\[S_{M_1-M_2}=\sqrt{\frac{2MSE}{\mathfrak{n} _h}}\]
donde\(\mathfrak{n} _h\) es la media armónica de los tamaños de muestra y se calcula de la siguiente manera:
\[\mathfrak{n} _h=\frac{2}{\tfrac{1}{\mathfrak{n_1}}+\tfrac{1}{\mathfrak{n_2}}}=\frac{2}{\tfrac{1}{3}+\tfrac{1}{2}}=2.4\]
y
\[S_{M_1-M_2}=\sqrt{\frac{(2)(1.333)}{2.4}}=1.054\]
Por lo tanto,
\[t = \frac{4-3}{1.054} = 0.949\]
y la de dos colas\(p = 0.413\).


