12.5: Comparaciones por pares
- Page ID
- 152029
Objetivos de aprendizaje
- Definir comparación por pares
- Describir el problema de hacer\(t\) pruebas entre todos los pares de medias
- Calcular la prueba Tukey HSD
- Explicar por qué la prueba de Tukey no debe considerarse necesariamente una prueba de seguimiento
Muchos experimentos están diseñados para comparar más de dos condiciones. Tomaremos como ejemplo el estudio de caso “Sonrisas y clemencia”. En este estudio se investigó el efecto de diferentes tipos de sonrisas sobre la indulgencia mostrada a una persona. Una manera obvia de proceder sería hacer una prueba t de la diferencia entre cada media de grupo y cada una de las otras medias del grupo. Este procedimiento conduciría a las seis comparaciones que se muestran en la Tabla\(\PageIndex{1}\).
| falso vs fieltro |  |
 |
| falso vs miserable |  |
 |
| falso vs neutro |  |
 |
| sentido vs miserable |  |
 |
| fieltro vs neutro |  |
 |
| miserable vs neutral |  |
 |
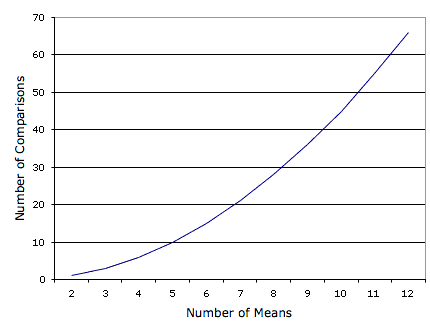
El problema con este enfoque es que si hicieras este análisis, tendrías seis posibilidades de cometer un error de Tipo I. Por lo tanto, si estuvieras usando el nivel de\(0.05\) significancia, la probabilidad de que hicieras un error de Tipo I en al menos una de estas comparaciones es mayor que\(0.05\). Cuantos más medios se comparan, más se infla la tasa de error de Tipo I. La figura\(\PageIndex{1}\) muestra el número de posibles comparaciones entre pares de medias (comparaciones por pares) en función del número de medias. Si solo hay dos medios, entonces solo se puede hacer una comparación. Si hay\(12\) medios, entonces hay\(66\) posibles comparaciones.
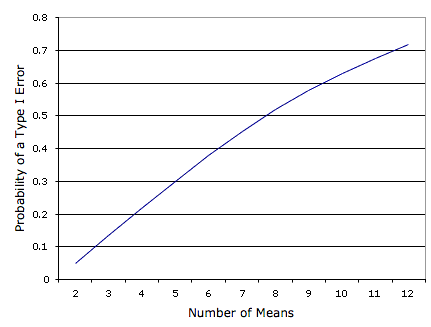
La figura\(\PageIndex{2}\) muestra la probabilidad de un error de Tipo I en función del número de medias. Como puedes ver, si tienes un experimento con\(12\) medias, la probabilidad es sobre\(0.70\) que al menos una de las\(66\) comparaciones entre medias sería significativa aunque todas las medias\(12\) poblacionales fueran las mismas.
La prueba de diferencia honestamente significativa de Tukey
La tasa de error Tipo I se puede controlar mediante una prueba llamada Prueba de Diferencia Honestamente Significativa de Tukey o Tukey HSD para abreviar. El HSD de Tukey se basa en una variación de la\(t\) distribución que toma en cuenta el número de medias que se comparan. Esta distribución se denomina distribución de rango studentized.
Volvamos al estudio de clemencia para ver cómo calcular la prueba HSD de Tukey. Verás que los cálculos son muy similares a los de una prueba t de grupos independientes. Los pasos se detallan a continuación:
- Calcular las medias y varianzas de cada grupo. A continuación se muestran.
| Condición | Media | Varianza |
|---|---|---|
| Falso | 5.37 | 3.34 |
| Fieltro | 4.91 | 2.83 |
| Desgraciado | 4.91 | 2.11 |
| Neutral | 4.12 | 2.32 |
- Compute\(MSE\), que es simplemente la media de las varianzas. Es igual a\(2.65\).
- Calcula\[Q=\frac{M_i-M_j}{\sqrt{\tfrac{MSE}{n}}}\] para cada par de medias, donde\(M_i\) es una media,\(M_j\) es la otra media, y\(n\) es el número de puntuaciones en cada grupo. Para estos datos, hay\(34\) observaciones por grupo. El valor en el denominador es\(0.279\).
- Calcule\(p\) para cada comparación usando la Calculadora de Rango Studentizado. Los grados de libertad son iguales al número total de observaciones menos el número de medias. Para este experimento,\(df = 136 - 4 = 132\).
Las pruebas para estos datos se muestran en la Tabla\(\PageIndex{2}\).
| Comparativa | M i -M j | Q | p |
|---|---|---|---|
| Falso - Fieltro | 0.46 | 1.65 | 0.649 |
| Falso - Desgraciado | 0.46 | 1.65 | 0.649 |
| Falso - Neutro | 1.25 | 4.48 | 0.010 |
| Fieltro - miserables | 0.00 | 0.00 | 1.000 |
| Fieltro - Neutro | 0.79 | 2.83 | 0.193 |
| Miserable - Neutral | 0.79 | 2.83 | 0.193 |
La única comparación significativa es entre la sonrisa falsa y la sonrisa neutra.
No es raro obtener resultados que en la superficie parezcan paradójicos. Por ejemplo, estos resultados parecen indicar que
- la falsa sonrisa es lo mismo que la sonrisa miserable,
- la sonrisa miserable es lo mismo que el control neutral, y
- la falsa sonrisa es diferente del control neutral.
Esta aparente contradicción se evita si tienes cuidado de no aceptar la hipótesis nula cuando no la rechazas. El hallazgo de que la falsa sonrisa no es significativamente diferente de la sonrisa miserable no significa que sean realmente iguales. Más bien significa que no hay pruebas convincentes de que sean diferentes. De igual manera, la diferencia no significativa entre la sonrisa miserable y el control no significa que sean iguales. La conclusión correcta es que la falsa sonrisa es más alta que el control y que la sonrisa miserable es o
- igual a la falsa sonrisa,
- igual al control, o
- en algún lugar intermedio.
Los supuestos de la prueba de Tukey son esencialmente los mismos que para una prueba t de grupos independientes: normalidad, homogeneidad de varianza y observaciones independientes. La prueba es bastante robusta ante violaciones de la normalidad. Violar la homogeneidad de varianza puede ser más problemático que en el caso de dos muestras ya que el\(MSE\) se basa en datos de todos los grupos. El supuesto de independencia de las observaciones es importante y no debe ser violado.
Análisis por Computación
Para la mayoría de los programas de computadora, debe formatear sus datos de la misma manera que lo hace para una prueba t de grupos independientes. La única diferencia es que si tienes, digamos, cuatro grupos, codificarías cada grupo como\(1\),,\(2\)\(3\), o más\(4\) bien que solo\(1\) o\(2\).
Aunque los programas de estadísticas con todas las funciones como SAS, SPSS, R y otros pueden calcular la prueba de Tukey, es posible que los programas más pequeños (incluido Analysis Lab) no. Sin embargo, estos programas son generalmente capaces de computar un procedimiento conocido como Análisis de Varianza (ANOVA). Este procedimiento se describirá en detalle en un capítulo posterior. Su relevancia aquí es que un ANOVA calcula el\(MSE\) que se utiliza en el cálculo de la prueba de Tukey. Por ejemplo, a continuación se muestra la tabla de resumen de ANOVA para los datos de “Sonrisas y indulgencia”.

La columna etiquetada MS significa “Mean Square” y por lo tanto el valor\(2.6489\) en la fila “Error” y la columna MS es el “Error cuadrático medio” o MSE. Recordemos que este es el mismo valor calculado aquí (\(2.65\)) cuando se redondea.
La prueba de Tukey no necesita ser un seguimiento del ANOVA
Algunos libros de texto introducen la prueba de Tukey solo como seguimiento a un análisis de varianza. No hay ninguna razón lógica o estadística por la que no deberías usar la prueba de Tukey incluso si no computas un ANOVA (o incluso sabes cuál es uno). Si usted o su instructor no desean tomar nuestra palabra para esto, vea el excelente artículo sobre este y otros temas en análisis estadístico de Leland Wilkinson y el Grupo de Trabajo sobre Inferencia Estadística de la Junta de Asuntos Científicos de la APA, publicado en el American Psicólogo, agosto de 1999, Vol. 54, No. 8, 594—604.
Cálculos para Tamaños de Muestra Desiguales (opcional)
El cálculo de\(MSE\) para tamaños de muestra desiguales es similar a su cálculo en una prueba t de grupos independientes. Estos son los pasos:
- Calcula un Error de Suma de Cuadrados (\(SSE\)) usando la siguiente fórmula\[SSE=\sum (X-M_1)^2+\sum (X-M_2)^2+\cdots +\sum (X-M_k)^2\] donde\(M_i\) es la media del\(i^{th}\) grupo y\(k\) es el número de grupos.
- Calcula los grados de error de libertad (\(dfe)\)restando el número de grupos (\(k\)) del número total de observaciones (\(N\)). Por lo tanto,\[dfe = N - k\]
- Calcular\(MSE\) dividiendo\(SSE\) por\(dfe\):\[MSE = \frac{SSE}{dfe}\]
- Para cada comparación de medias, utilice la media armónica de la\(n's\) para las dos medias (\(\mathfrak{n_h}\)).
Todos los demás aspectos de los cálculos son los mismos que cuando se tienen tamaños de muestra iguales.


