12.7: Pares correlacionados
- Page ID
- 152030
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Determine si tiene pares correlacionados o grupos independientes
- Cálculo de una prueba t para pares correlacionados
Consideremos cómo analizar los datos del estudio de caso “Tratamiento del TDAH”. Estos datos consisten en las puntuaciones de\(24\) niños con TDAH en una tarea de retraso de gratificación (DOG). Cada niño fue probado bajo cuatro niveles de dosificación. En esta sección, nos ocuparemos únicamente de probar la diferencia entre la media de la condición placebo (\(D0\)) y la media de la condición de dosis más alta (\(D60\)). La primera pregunta es por qué la diferencia entre medias no debe probarse utilizando el procedimiento descrito en la sección Diferencia entre dos medias (grupos independientes). La respuesta radica en el hecho de que en este experimento no tenemos grupos independientes. Los puntajes en la\(D0\) condición son de los mismos sujetos que los puntajes en la\(D60\) condición. Solo hay un grupo de sujetos, cada sujeto siendo probado tanto en\(D0\) las\(D60\) condiciones como.
La figura\(\PageIndex{1}\) muestra una gráfica de dispersión de las puntuaciones\(60\) -mg (\(D60\)) en función de las puntuaciones de\(0\) -mg (\(D0\)). Es claro que los niños que se vuelven más correctos en la\(D0\) condición tienden a ser más correctos en la\(D60\) condición. La correlación entre las dos condiciones es alta:\(r = 0.80\). Claramente estas dos variables no son independientes.
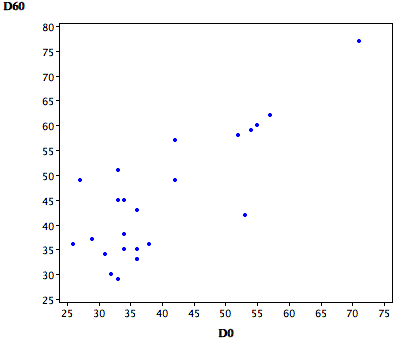
Cálculos
Tal vez recuerde que el método para probar la diferencia entre estas medias se presentó en la sección “Probando una Media Única”. El procedimiento computacional consiste en calcular la diferencia entre las condiciones\(D60\) y las\(D0\) condiciones para cada hijo y probar si la diferencia media es significativamente diferente de\(0\). Las puntuaciones de diferencia se muestran en la Tabla\(\PageIndex{1}\). Como se muestra en la sección sobre la prueba de una sola media, la puntuación de diferencia media es la\(4.96\) que es significativamente diferente de\(0\):\(t = 3.22,\; df = 23,\; p = 0.0038\). Esta\(t\) prueba tiene varios nombres incluyendo "\(t\)prueba correlacionada" y "\(t\)prueba de pares relacionados”.
En general, la\(t\) prueba correlacionada se calcula calculando primero la diferencia entre las dos puntuaciones para cada asignatura. Entonces, se computa una prueba de una sola media sobre la media de estas puntuaciones de diferencia.
| D0 | D60 | D60-D0 |
|---|---|---|
| 57 | 62 | 5 |
| 27 | 49 | 22 |
| 32 | 30 | -2 |
| 31 | 34 | 3 |
| 34 | 38 | 4 |
| 38 | 36 | -2 |
| 71 | 77 | 6 |
| 33 | 51 | 18 |
| 34 | 45 | 11 |
| 53 | 42 | -11 |
| 36 | 43 | 7 |
| 42 | 57 | 15 |
| 26 | 36 | 10 |
| 52 | 58 | 6 |
| 36 | 35 | -1 |
| 55 | 60 | 5 |
| 36 | 33 | -3 |
| 42 | 49 | 7 |
| 36 | 33 | -3 |
| 54 | 59 | 5 |
| 34 | 35 | 1 |
| 29 | 37 | 8 |
| 33 | 45 | 12 |
| 33 | 29 | -4 |
Si hubieras usado erróneamente el método para una\(t\) prueba de grupos independientes con estos datos, habrías encontrado que\(t = 1.42\),\(df = 46\), y\(p = 0.15\). Es decir, no se habría encontrado que la diferencia entre medias fuera estadísticamente significativa. Este es un resultado típico:\(t\) las pruebas correlacionadas casi siempre tienen mayor poder que\(t\) las pruebas de grupos independientes. Esto se debe a que en\(t\) pruebas correlacionadas, cada puntaje de diferencia es una comparación del desempeño en una condición con el desempeño de ese mismo sujeto en otra condición. Esto hace que cada sujeto sea “su propio control” y evita que las diferencias entre sujetos entren en el análisis. El resultado es que el error estándar de la diferencia entre medias es menor en la\(t\) prueba correlacionada y, dado que este término está en el denominador de la fórmula para\(t\), da como resultado una mayor\(t\).
Detalles sobre el Error Estándar de la Diferencia entre Medias (Opcional)
Para ver por qué el error estándar de la diferencia entre medias es menor en una\(t\) prueba correlacionada, considere la varianza de las puntuaciones de diferencia. Como se muestra en la sección sobre la Ley de Suma de Varianza, la varianza de la suma o diferencia de las dos variables\(X\) y\(Y\) es:
\[S_{X\pm Y}^{2} = S_{X}^{2} + S_{Y}^{2} \pm 2rS_XS_Y\]
Por lo tanto, la varianza de las puntuaciones de diferencia es la varianza en la primera condición (\(X\)) más la varianza en la segunda condición (\(Y\)) menos el doble del producto de
- la correlación,
- la desviación estándar de\(X\), y
- la desviación estándar de\(Y\). Para el ejemplo actual,\(r = 0.80\) y las varianzas y desviaciones estándar se muestran en la Tabla\(\PageIndex{2}\).
| D0 | D60 | D60 - D0 | |
|---|---|---|---|
| Varianza | 128.02 | 151.78 | 56.82 |
| Sd | 11.31 | 12.32 | 7.54 |
La varianza de las puntuaciones de diferencia de se\(56.82\) puede calcular como:
\[128.02 + 151.78 - (2)(0.80)(11.31)(12.32)\]
que es igual a\(56.82\) excepción del error de redondeo. Observe que cuanto mayor sea la correlación, menor será el error estándar de la media.


