12.E: Pruebas de Medios (Ejercicios)
- Page ID
- 152023
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Preguntas Generales
Q1
Los puntajes de una muestra aleatoria de\(8\) estudiantes en una prueba de física son los siguientes:\(60, 62, 67, 69, 70, 72, 75, 78\).
- Prueba para ver si la media de la muestra es significativamente diferente\(65\) a la del\(0.05\) nivel. Informar los\(p\) valores\(t\) y.
- La investigadora se da cuenta de que accidentalmente registró la partitura que debería haber sido\(76\) como\(67\). ¿Estas puntuaciones corregidas son significativamente diferentes de las del\(65\)\(0.05\) nivel? (sección pertinente)
Q2
Se realiza un experimento (hipotético) sobre el efecto del alcohol en la capacidad motora perceptual. Diez sujetos son evaluados cada uno dos veces, una después de tomar dos bebidas y otra después de tomar dos vasos de agua. Las dos pruebas fueron en dos días diferentes para darle al alcohol una oportunidad de desgastarse. A la mitad de los sujetos se les administró alcohol primero y a la mitad se les dio agua primero. A continuación se muestran las puntuaciones de las\(10\) asignaturas. El primer número para cada asignatura es su desempeño en la condición “agua”. Las puntuaciones más altas reflejan un mejor desempeño. Prueba para ver si el alcohol tuvo un efecto significativo. Informar los\(p\) valores\(t\) y. (sección pertinente)
|
agua |
alcohol |
|
16 |
13 |
|
15 |
13 |
|
11 |
10 |
|
20 |
18 |
|
19 |
17 |
|
14 |
11 |
|
13 |
10 |
|
15 |
15 |
|
14 |
11 |
|
16 |
16 |
Q3
A continuación se muestran las puntuaciones en una prueba de vocabulario (hipotética) de un grupo de\(20\) niños de un\(60\) año y un grupo de niños de un año.
|
20 años |
60 años |
|
27 |
26 |
|
26 |
29 |
|
21 |
29 |
|
24 |
29 |
|
15 |
27 |
|
18 |
16 |
|
17 |
20 |
|
12 |
27 |
|
13 |
- Pruebe la diferencia de medias para la significancia usando el\(0.05\) nivel. (sección pertinente).
- Enumere los supuestos hechos al computar su respuesta. (sección pertinente)
Q4
La distribución muestral de un estadístico se distribuye normalmente con un error estándar estimado de\(12\), (\(df = 20)\).
- ¿Cuál es la probabilidad de que hubieras obtenido una media de\(107\) (o más extrema) si el parámetro poblacional fuera\(100\)? ¿Esta probabilidad es significativa en el\(0.05\) nivel (de dos colas)?
- ¿Cuál es la probabilidad de que hubieras obtenido una media de\(95\) o menos (de una cola)? ¿Esta probabilidad es significativa a\(0.05\) nivel? Es posible que desee utilizar la calculadora de distribución t para este problema. (sección pertinente)
Q5
¿Cómo se decide si se usa una\(t\) prueba de grupos independientes o una\(t\) prueba correlacionada (prueba de medias dependientes)? (sección relevante y sección relevante)
Q6
Un experimento comparó la capacidad de tres grupos de sujetos para recordar posiciones de ajedrez presentadas brevemente. Los datos se muestran a continuación.
|
No jugadores |
Principiantes |
Jugadores del torneo |
|
22.1 |
32.5 |
40.1 |
|
22.3 |
37.1 |
45.6 |
|
26.2 |
39.1 |
51.2 |
|
29.6 |
40.5 |
56.4 |
|
31.7 |
45.5 |
58.1 |
|
33.5 |
51.3 |
71.1 |
|
38.9 |
52.6 |
74.9 |
|
39.7 |
55.7 |
75.9 |
|
43.2 |
55.9 |
80.3 |
|
43.2 |
57.7 |
85.3 |
- Mediante el procedimiento Tukey HSD, determinar qué grupos son significativamente diferentes entre sí en el\(0.05\) nivel. (sección pertinente)
- Ahora compara cada par de grupos usando\(t\) -tests. Asegúrese de controlar la tasa de error familiar (at\(0.05\)) usando la corrección de Bonferroni. Especifique el nivel alfa que utilizó.
Q7
A continuación se presentan datos que muestran los resultados de seis sujetos en una prueba de memoria. Los tres puntajes por materia son sus puntuaciones en tres ensayos (\(a\),\(b\), y\(c\)) de una tarea de memoria. ¿Están mejorando los sujetos en cada ensayo? Probar el efecto lineal del ensayo para los datos.
|
a |
b |
c |
|
4 |
6 |
7 |
|
3 |
7 |
8 |
|
2 |
8 |
5 |
|
1 |
4 |
7 |
|
4 |
6 |
9 |
|
2 |
4 |
2 |
- Calcular\(L\) para cada sujeto usando los pesos de contraste\(-1\),\(0\), y\(1\). Es decir, computar\((-1)(a) + (0)(b) + (1)(c)\) para cada materia.
- Calcule una\(t\) prueba de una muestra en esta columna (con los\(L\) valores para cada tema) que haya creado. (sección pertinente)
Q8
Los participantes lanzaron dardos a un objetivo. En una condición, usaron su mano preferida; en la otra condición, usaron su otra mano. Todos los sujetos se realizaron en ambas condiciones (se contrapesó el orden de las condiciones). Sus puntuaciones se muestran a continuación.
|
Preferido |
No preferido |
|
12 |
7 |
|
7 |
9 |
|
11 |
8 |
|
13 |
10 |
|
10 |
9 |
- ¿Qué tipo\(t\) de prueba se debe usar?
- Calcular los\(p\) valores de dos colas\(t\) y utilizando esta\(t\) prueba.
- Calcular los\(p\) valores de una cola\(t\) y usando esta\(t\) prueba.
Q9
Supongamos que los datos del problema anterior fueron recolectados utilizando dos grupos diferentes de sujetos: Un grupo utilizó su mano preferida y el otro grupo utilizó su mano no preferida. Analizar los datos y comparar los resultados con los del problema anterior (sección relevante)
Q10
Tienes\(4\) medios, y quieres comparar cada media con cada otra media.
- ¿Cuántas pruebas totales vas a computar?
- ¿Cuál sería la posibilidad de hacer al menos un error de Tipo I si el error de Tipo I para cada prueba fuera\(0.05\) y las pruebas fueran independientes? (sección relevante y sección relevante)
- ¿Son independientes las pruebas y cómo afecta la independencia/no independencia a la probabilidad en (b).
Q11
En un experimento, los participantes se dividieron en\(4\) grupos. Hubo\(20\) participantes en cada grupo, por lo que los grados de libertad (error) para este estudio fueron\(80 - 4 = 76\). Se realizó la prueba HSD de Tukey sobre los datos.
- Calcula el\(p\) valor para cada par con base en el\(Q\) valor que se da a continuación. Querrás usar la Calculadora de Rango Estudentizado.
- ¿Qué diferencias son significativas a\(0.05\) nivel? (sección pertinente)
|
Comparación de Grupos |
Q |
|
A - B |
3.4 |
|
A - C |
3.8 |
|
A - D |
4.3 |
|
B - C |
1.7 |
|
B - D |
3.9 |
|
C - D |
3.7 |
Q12
Si tienes\(5\) grupos en tu estudio, ¿por qué no deberías simplemente calcular una\(t\) prueba de la media de cada grupo con la media del otro grupo? (sección pertinente)
Q13
Estás realizando un estudio para ver si a los estudiantes les va mejor cuando estudian todos a la vez o en intervalos. Un grupo de\(12\) participantes realizó una prueba después de estudiar durante una hora de manera continua. El otro grupo de\(12\) participantes realizó una prueba después de estudiar durante tres sesiones de veinte minutos. El primer grupo tuvo una puntuación media de\(75\) y una varianza de\(120\). El segundo grupo tuvo una puntuación media de\(86\) y una varianza de\(100\).
- ¿Cuál es el\(t\) valor calculado? ¿Los puntajes medios de los exámenes de estos dos grupos son significativamente diferentes a\(0.05\) nivel?
- ¿Cuál sería el\(t\) valor si solo hubiera\(6\) participantes en cada grupo? ¿Los puntajes serían significativos a\(0.05\) nivel?
Q14
Se diseñó una nueva prueba para tener una media de\(80\) y una desviación estándar de\(10\). Una muestra aleatoria de\(20\) alumnos de tu escuela toma el examen, y la puntuación media resulta ser\(85\). ¿Esta puntuación difiere significativamente de\(80\)? Para responder a este problema, es posible que desee utilizar la Calculadora de Distribución Normal. (sección pertinente)
Q15
Se realiza una\(t\) prueba de una muestra y se calcula una\(t\) estadística de\(3.0\). La media de su muestra fue\(1.3\) y la desviación estándar fue\(2.6\). ¿Cuántos participantes se utilizaron en este estudio? (sección pertinente)
Q16
Verdadero/falso: Los contrastes\((-3, 1 1 1)\) y\((0, 0 , -1, 1)\) son ortogonales. (sección pertinente)
Q17
Verdadero/falso: Si estás haciendo\(4\) comparaciones entre medias, entonces con base en la corrección de Bonferroni, debes usar un nivel alfa de\(0.01\) para cada prueba. (sección pertinente)
Q18
Verdadero/falso:\(t\) Las pruebas correlacionadas casi siempre tienen mayor poder que\(t\) las pruebas independientes. (sección pertinente)
Q19
Verdadero/falso: La gráfica a continuación representa una violación de la hipótesis de homogeneidad de varianza. (sección pertinente)
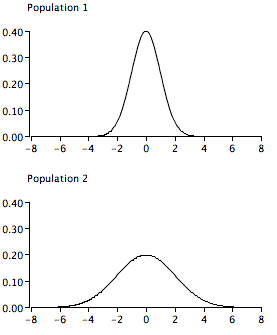
Q20
Verdadero/falso: Cuando estás realizando una\(t\) prueba de una muestra y conoces la desviación estándar de la población, buscas el\(t\) valor crítico en la tabla en función de los grados de libertad. (sección pertinente)
Preguntas de casos prácticos
Las siguientes preguntas utilizan datos del estudio de caso Angry Moods (AM).
Q21
(AM #17) ¿Los atletas o no atletas se calman más cuando están enojados? Realizar una\(t\) prueba para ver si la diferencia entre grupos en los puntajes de Control-In es estadísticamente significativa.
Q22
¿La gente en general tiene una puntuación más alta de Anger-Out o Anger-In? Realizar una\(t\) prueba sobre la diferencia entre medias de estos dos puntajes. ¿Son estos dos medios independientes o dependientes? (sección pertinente)
Las siguientes preguntas utilizan datos del estudio de caso Sonrisas y Leniencia (SL).
Q23
Comparar cada media con la media neutra. Asegúrese de controlar la tasa de error familiar. (sección pertinente)
Q24
¿Una “sonrisa sentida” lleva a más indulgencia que otros tipos de sonrisas?
- Calcular\(L\) (la combinación lineal) usando los siguientes pesos de contraste\(false: -1,\; felt: 2,\; miserable: -1,\; neutral: 0\).
- Realizar una prueba de significancia sobre este valor de\(L\). (sección pertinente)
Las siguientes preguntas son del estudio de caso Animal Research (AR).
Q25
(AR #8) Realizar una\(t\) prueba de muestras independiente comparando machos con hembras con la creencia de que la investigación animal es necesaria. (sección pertinente)
Q26
(AR #9) Con base en la\(t\) prueba que realizaste en el problema anterior, ¿eres capaz de rechazar la hipótesis nula si\(alpha = 0.05\)? ¿Y si\(alpha = 0.1\)? (sección pertinente)
Q27
(AR #10) ¿Hay alguna evidencia de que el supuesto de\(t\) prueba de homogeneidad de varianza se viola en la\(t\) prueba que computó en #25? (sección pertinente)
Las siguientes preguntas utilizan datos del estudio de caso Tratamiento del TDAH (AT).
Q28
Compare cada dosis con la dosis por debajo de ella (compare\(d0\) y\(d15\),\(d15\) y\(d30\), y y\(d30\) y\(d60\)). Recuerde que los pacientes completaron la tarea después de cada dosis.
- Si la tasa de error familiar es\(0.05\), ¿cuál es el nivel alfa que usarás para cada comparación al hacer la corrección de Bonferroni?
- ¿Qué diferencias son significativas en este nivel? (sección pertinente)
Q29
¿El rendimiento aumenta linealmente con la dosis?
- Trazar un gráfico de líneas de estos datos.
- Cómputos\(L\) para cada paciente. Para ello, crea una nueva variable donde multipliques los siguientes coeficientes por sus dosis correspondientes y luego se suma el total:\((-3)d0 + (-1)d15 + (1)d30 + (3)d60\) (ver #8). ¿Cuál es la media de\(L\)?
- Realizar una prueba de significancia en\(L\). Calcular el intervalo de\(95\%\) confianza para\(L\). (sección pertinente)
Seleccionar respuestas
S1
- \(t(7) = 1.91\)
S4
- \(0.035\)
S7
- de dos colas\(p = 0.0088\)
S8
- \(p = 0.1662\)
S11
- \(A - B: p = 0.085\)
S13
- \(t(22) = 2.57\)
S23
\(t(76) = 3.04\)
S25
- \(p = 0.0745\)
S29
- \(p = 0.0006\)


