14.4: Error estándar de la estimación
- Page ID
- 152308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Hacer juicios sobre el tamaño del error estándar de la estimación a partir de una gráfica de dispersión
- Calcular el error estándar de la estimación basado en errores de predicción
- Calcular el error estándar usando la correlación de Pearson
- Estimar el error estándar de la estimación con base en una muestra
La figura\(\PageIndex{1}\) muestra dos ejemplos de regresión. Se puede ver que en\(\text{Graph A}\), los puntos están más cerca de la línea de lo que están en\(\text{Graph B}\). Por lo tanto, las predicciones en\(\text{Graph A}\) son más precisas que en\(\text{Graph B}\).
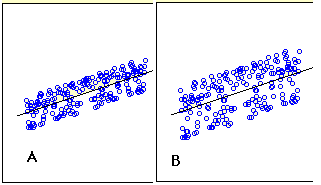
El error estándar de la estimación es una medida de la precisión de las predicciones. Recordemos que la línea de regresión es la línea que minimiza la suma de las desviaciones cuadradas de predicción (también llamada el error de suma de cuadrados). El error estándar de la estimación está estrechamente relacionado con esta cantidad y se define a continuación:
\[\sigma _{est}=\sqrt{\frac{\sum (Y-Y')^2}{N}}\]
donde\(\sigma _{est}\) está el error estándar de la estimación,\(Y\) es una puntuación real,\(Y'\) es una puntuación predicha, y\(N\) es el número de pares de puntuaciones. El numerador es la suma de las diferencias al cuadrado entre las puntuaciones reales y las puntuaciones predichas.
Observe la similitud de la fórmula para\(\sigma _{est}\) a la fórmula para σ. Resulta que σest es la desviación estándar de los errores de predicción (cada uno\(Y - Y'\) es un error de predicción).
Supongamos que los datos en la Tabla\(\PageIndex{1}\) son los datos de una población de cinco\(X\),\(Y\) pares.
| X | Y | Y' | Y-Y' | (Y-Y') 2 | |
|---|---|---|---|---|---|
| 1.00 | 1.00 | 1.210 | -0.210 | 0.044 | |
| 2.00 | 2.00 | 1.635 | 0.365 | 0.133 | |
| 3.00 | 1.30 | 2.060 | -0.760 | 0.578 | |
| 4.00 | 3.75 | 2.485 | 1.265 | 1.600 | |
| 5.00 | 2.25 | 2.910 | -0.660 | 0.436 | |
| Suma | 15.00 | 10.30 | 10.30 | 0.000 | 2.791 |
La última columna muestra que la suma de los errores cuadrados de predicción es\(2.791\). Por lo tanto, el error estándar de la estimación es
\[\sigma _{est}=\sqrt{\frac{2.791}{5}}=0.747\]
Existe una versión de la fórmula para el error estándar en términos de correlación de Pearson:
\[\sigma _{est}=\sqrt{\frac{(1-\rho )^2SSY}{N}}\]
donde\(ρ\) está el valor poblacional de la correlación de Pearson y\(SSY\) es
\[SSY=\sum (Y-\mu _Y)^2\]
Para los datos en la Tabla\(\PageIndex{1}\),\(μ_Y = 2.06\),\(SSY = 4.597\) y\(ρ= 0.6268\). Por lo tanto,
\[\sigma _{est}=\sqrt{\frac{(1-0.6268^2)(4.597)}{5}}=\sqrt{\frac{2.791}{5}}=0.747\]
que es el mismo valor calculado anteriormente.
Se utilizan fórmulas similares cuando el error estándar de la estimación se calcula a partir de una muestra en lugar de una población. La única diferencia es que el denominador es\(N-2\) más que\(N\). La razón\(N-2\) se utiliza más que\(N-1\) es que se estimaron dos parámetros (la pendiente y la intersección) para estimar la suma de cuadrados. A continuación se muestran las fórmulas para una muestra comparable a las de una población.
\[s _{est}=\sqrt{\frac{\sum (Y-Y')^2}{N-2}}\]
\[s _{est}=\sqrt{\frac{2.791}{3}}=0.964\]
\[s _{est}=\sqrt{\frac{(1-r)^2SSY}{N-2}}\]


