14.8: Introducción a la Regresión Múltiple
- Page ID
- 152321
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Indicar la ecuación de regresión
- Definir “coeficiente de regresión”
- Definir “peso beta”
- Explicar qué\(R\) es y cómo se relaciona con\(r\)
- Explicar por qué un peso de regresión se llama “pendiente parcial”
- Explicar por qué la suma de cuadrados explicada en un modelo de regresión múltiple suele ser menor que la suma de las sumas de cuadrados en regresión simple
- Definir\(R^2\) en términos de proporción explicada
- Prueba\(R^2\) de significancia
- Probar la diferencia entre un modelo completo y un modelo reducido para determinar la significancia
- Declarar los supuestos de regresión múltiple y especificar qué aspectos del análisis requieren supuestos
En regresión lineal simple, se predice una variable criterio a partir de una variable predictora. En regresión múltiple, el criterio es pronosticado por dos o más variables. Por ejemplo, en el estudio de caso del SAT, es posible que desee predecir el promedio de calificaciones universitarias de un estudiante sobre la base de su GPA de secundaria (\(HSGPA\)) y su puntaje total del SAT (verbal + matemáticas). La idea básica es encontrar una combinación lineal de\(HSGPA\) y\(SAT\) que mejor prediga GPA Universitario (\(UGPA\)). Es decir, el problema es encontrar los valores de\(b_1\) y\(b_2\) en la ecuación que se muestra a continuación que den las mejores predicciones de\(UGPA\). Al igual que en el caso de la regresión lineal simple, definimos las mejores predicciones como las predicciones que minimizan los errores cuadrados de predicción.
\[UGPA' = b_1HSGPA + b_2SAT + A\]
donde\(UGPA'\) es el valor predicho de GPA Universitario y\(A\) es una constante. Para estos datos, la mejor ecuación de predicción se muestra a continuación:
\[UGPA' = 0.541 \times HSGPA + 0.008 \times SAT + 0.540\]
En otras palabras, para calcular la predicción del GPA universitario de un estudiante, se suma su GPA de secundaria multiplicado por\(0.541\), su\(SAT\) multiplicado por\(0.008\), y\(0.540\). \(\PageIndex{1}\)La tabla muestra los datos y predicciones para los cinco primeros estudiantes en el conjunto de datos.
| HSGPA | SAT | UGPA' |
|---|---|---|
| 3.45 | 1232 | 3.38 |
| 2.78 | 1070 | 2.89 |
| 2.52 | 1086 | 2.76 |
| 3.67 | 1287 | 3.55 |
| 3.24 | 1130 | 3.19 |
Los valores de\(b\) (\(b_1\)y\(b_2\)) a veces se denominan “coeficientes de regresión” y a veces se denominan “pesos de regresión”. Estos dos términos son sinónimos.
La correlación múltiple (\(R\)) es igual a la correlación entre las puntuaciones predichas y las puntuaciones reales. En este ejemplo, es la correlación entre\(UGPA'\) y\(UGPA\), la que resulta ser\(0.79\). Es decir,\(R = 0.79\). Obsérvese que nunca\(R\) será negativo ya que si existen correlaciones negativas entre las variables predictoras y el criterio, los pesos de regresión serán negativos para que la correlación entre las puntuaciones pronosticadas y reales sea positiva.
Interpretación de los coeficientes de regresión
Un coeficiente de regresión en regresión múltiple es la pendiente de la relación lineal entre la variable criterio y la parte de una variable predictora que es independiente de todas las demás variables predictoras. En este ejemplo, el coeficiente de regresión para se\(HSGPA\) puede calcular prediciendo primero\(HSGPA\) desde\(SAT\) y guardando los errores de predicción (las diferencias entre\(HSGPA\) y\(HSGPA'\)). Estos errores de predicción se denominan “residuales” ya que son lo que queda en\(HSGPA\) después de que\(SAT\) se restan las predicciones de, y representan la parte de la\(HSGPA\) que es independiente\(SAT\). Estos residuos se conocen como\(HSGPA.SAT\), lo que significa que son los residuales en\(HSGPA\) después de haber sido predichos por\(SAT\). La correlación entre\(HSGPA.SAT\) y\(SAT\) es necesariamente\(0\).
El paso final en el cálculo del coeficiente de regresión es encontrar la pendiente de la relación entre estos residuos y\(UGPA\). Esta pendiente es el coeficiente de regresión para\(HSGPA\). La siguiente ecuación se utiliza para predecir a\(HSGPA\) partir de\(SAT\):
\[HSGPA' = -1.314 + 0.0036 \times SAT\]
Los residuos se calculan entonces como:
\[HSGPA - HSGPA'\]
La ecuación de regresión lineal para la predicción de\(UGPA\) por los residuales es
\[UGPA' = 0.541 \times HSGPA.SAT + 3.173\]
Observe que la pendiente (\(0.541\)) es el mismo valor dado anteriormente para\(b_1\) en la ecuación de regresión múltiple.
Esto significa que el coeficiente de regresión para\(HSGPA\) es la pendiente de la relación entre la variable criterio y la parte de la\(HSGPA\) misma es independiente de (no correlacionada con) las otras variables predictoras. Representa el cambio en la variable criterio asociado con un cambio de uno en la variable predictora cuando todas las demás variables predictoras se mantienen constantes. Dado que el coeficiente de regresión para\(HSGPA\) es\(0.54\), esto significa que, manteniéndose\(SAT\) constante, un cambio de uno en\(HSGPA\) se asocia con un cambio de\(0.54\) in\(UGPA'\). Si dos estudiantes tuvieran lo mismo\(SAT\) y difirieran en\(HSGPA\) por\(2\), entonces usted predeciría que diferirían en\(UGPA\) por\((2)(0.54) = 1.08\). Del mismo modo, si difirieran por\(0.5\), entonces usted predeciría que diferirían por\((0.50)(0.54) = 0.27\).
La pendiente de la relación entre la parte de una variable predictora independiente de otras variables predictoras y el criterio es su pendiente parcial. Así, el coeficiente de regresión de\(0.541\) for\(HSGPA\) y el coeficiente de regresión de\(0.008\) for\(SAT\) son pendientes parciales. Cada pendiente parcial representa la relación entre la variable predictora y el criterio manteniendo constantes todas las demás variables predictoras.
Es difícil comparar los coeficientes para diferentes variables directamente porque se miden en diferentes escalas. Una diferencia de\(1\) in\(HSGPA\) es una diferencia bastante grande, mientras que una diferencia de\(1\) en el\(SAT\) es insignificante. Por lo tanto, puede ser ventajoso transformar las variables para que estén en la misma escala. El enfoque más directo es estandarizar las variables para que cada una de ellas tenga una desviación estándar de\(1\). Un peso de regresión para variables estandarizadas se denomina “peso beta” y se designa con la letra griega\(β\). Para estos datos, los pesos beta son\(0.625\) y\(0.198\). Estos valores representan el cambio en el criterio (en desviaciones estándar) asociado con un cambio de una desviación estándar en un predictor [manteniendo constante el valor o valores en el otro predictor (es)]. Claramente, un cambio de una desviación estándar en\(HSGPA\) se asocia con una diferencia mayor que un cambio de una desviación estándar de\(SAT\). En términos prácticos, esto significa que si conoces a un alumno\(HSGPA\), conocer el del alumno\(SAT\) no ayuda a la predicción de\(UGPA\) mucho. No obstante, si no conoces el del alumno\(HSGPA\), el suyo\(SAT\) puede ayudar en la predicción ya que el\(β\) peso en la regresión simple que predice\(UGPA\) desde\(SAT\) es\(0.68\). Para fines de comparación, el\(β\) peso en la regresión simple que predice a\(UGPA\) partir de\(HSGPA\) es\(0.78\). Como suele ser el caso, las pendientes parciales son más pequeñas que las pendientes en regresión simple.
Partición de las Sumas de Cuadrados
Al igual que en el caso de la regresión lineal simple, la suma de cuadrados para el criterio (\(UGPA\)en este ejemplo) se puede dividir en la suma de cuadrados predichos y la suma de cuadrados del error. Es decir,
\[SSY = SSY' + SSE\]
que para estos datos:
\[20.798 = 12.961 + 7.837\]
La suma de cuadrados pronosticados también se conoce como la “suma de cuadrados explicada”. Nuevamente, como en el caso de la regresión simple,
\[\text{Proportion Explained} = SSY'/SSY\]
En regresión simple, la proporción de varianza explicada es igual a\(r^2\); en regresión múltiple, la proporción de varianza explicada es igual a\(R^2\).
En regresión múltiple, a menudo es informativo dividir la suma de cuadrados explicada entre las variables predictoras. Por ejemplo, la suma de cuadrados explicados para estos datos es\(12.96\). ¿Cómo se divide este valor entre\(HSGPA\) y\(SAT\)? Un enfoque que, como se verá, no funciona es predecir\(UGPA\) por separado regresiones simples para\(HSGPA\) y\(SAT\). Como puede verse en la Tabla\(\PageIndex{2}\), la suma de cuadrados en estas regresiones simples separadas es\(12.64\) para\(HSGPA\) y\(9.75\) para\(SAT\). Si sumamos estas dos sumas de cuadrados obtenemos\(22.39\), un valor mucho mayor que la suma de cuadrados explicada\(12.96\) en el análisis de regresión múltiple. La explicación es que\(HSGPA\) y\(SAT\) están altamente correlacionados (\(r = 0.78\)) y por lo tanto gran parte de la varianza en\(UGPA\) se confunde entre\(HSGPA\) y\(SAT\). Es decir, podría explicarse por cualquiera\(HSGPA\) o\(SAT\) y se cuenta dos veces si las sumas de cuadrados para\(HSGPA\) y simplemente\(SAT\) se suman.
| Predictores | Suma de Cuadrados |
|---|---|
| HSGPA | 12.64 |
| SAT | 9.75 |
| HSGPA y SAT | 12.96 |
\(\PageIndex{3}\)La tabla muestra la partición de la suma de cuadrados en la suma de cuadrados explicada de manera única por cada variable predictora, la suma de cuadrados confundida entre las dos variables predictoras y la suma de cuadrados de error. De esta tabla se desprende que la mayor parte de la suma de cuadrados explicados se confunde entre\(HSGPA\) y\(SAT\). Obsérvese que la suma de cuadrados explicada de manera única por una variable predictora es análoga a la pendiente parcial de la variable en que ambos implican la relación entre la variable y el criterio con la otra (s) variable (s) controlada (s).
| Fuente | Suma de Cuadrados | Proporción |
|---|---|---|
| HSGPA (único) | 3.21 | 0.15 |
| SAT (único) | 0.32 | 0.02 |
| HSGPA y SAT (Confundados) | 9.43 | 0.45 |
| Error | 7.84 | 0.38 |
| Total | 20.80 | 1.00 |
La suma de cuadrados atribuible únicamente a una variable se calcula comparando dos modelos de regresión: el modelo completo y un modelo reducido. El modelo completo es la regresión múltiple con todas las variables predictoras incluidas (\(HSGPA\)y\(SAT\) en este ejemplo). Un modelo reducido es un modelo que deja fuera una de las variables predictoras. La suma de cuadrados atribuible únicamente a una variable es la suma de cuadrados para el modelo completo menos la suma de cuadrados para el modelo reducido en el que se omite la variable de interés. Como se muestra en la Tabla\(\PageIndex{2}\), la suma de cuadrados para el modelo completo (\(HSGPA\)y\(SAT\)) es\(12.96\). La suma de cuadrados para el modelo reducido en el que\(HSGPA\) se omite es simplemente la suma de cuadrados explicada usando\(SAT\) como variable predictora y es\(9.75\). Por lo tanto, la suma de cuadrados atribuible singularmente a\(HSGPA\) es\(12.96 - 9.75 = 3.21\). De igual manera, la suma de cuadrados atribuible de manera única a\(SAT\) es\(12.96 - 12.64 = 0.32\). La suma confundida de cuadrados en este ejemplo se calcula restando la suma de cuadrados atribuible únicamente a las variables predictoras de la suma de cuadrados para el modelo completo:\(12.96 - 3.21 - 0.32 = 9.43\). El cálculo de las sumas confundidas de cuadrados en análisis con más de dos predictores es más complejo y está fuera del alcance de este texto.
Dado que la varianza es simplemente la suma de cuadrados dividida por los grados de libertad, es posible referirse a la proporción de varianza explicada de la misma manera que la proporción de la suma de cuadrados explicada. Es ligeramente más común referirse a la proporción de varianza explicada que a la proporción de la suma de cuadrados explicada y, por lo tanto, esa terminología se adoptará frecuentemente aquí.
Cuando las variables están altamente correlacionadas, la varianza explicada de manera única por las variables individuales puede ser pequeña aunque la varianza explicada por las variables tomadas en conjunto sea grande. Por ejemplo, aunque las proporciones de varianza explicadas de manera única por\(HSGPA\)\(0.15\) y\(SAT\) son solo y\(0.02\) respectivamente, juntas estas dos variables explican\(0.62\) la varianza. Por lo tanto, fácilmente podría subestimar la importancia de las variables si solo se considera la varianza explicada de manera única por cada variable. En consecuencia, a menudo es útil considerar un conjunto de variables relacionadas. Por ejemplo, supongamos que estabas interesado en predecir el desempeño laboral a partir de un gran número de variables algunas de las cuales reflejan la capacidad cognitiva. Es probable que estas medidas de capacidad cognitiva estén altamente correlacionadas entre sí y por lo tanto ninguna de ellas explicaría gran parte de la varianza independientemente de las otras variables. Sin embargo, se podría evitar este problema determinando la proporción de varianza explicada por todas las variables de capacidad cognitiva consideradas juntas como un conjunto. La varianza explicada por el conjunto incluiría toda la varianza explicada de manera única por las variables del conjunto así como toda la varianza confundida entre las variables del conjunto. No incluiría varianza confundida con variables fuera del conjunto. En definitiva, estarías calculando la varianza explicada por el conjunto de variables que es independiente de las variables que no están en el conjunto.
Estadísticas Inferenciales
Comenzamos presentando la fórmula para probar la significancia de la contribución de un conjunto de variables. Luego mostraremos cómo los casos especiales de esta fórmula pueden ser utilizados para probar la significancia de así\(R^2\) como para probar la significancia de la contribución única de las variables individuales.
El primer paso es calcular dos análisis de regresión:
- un análisis en el que se incluyen todas las variables predictoras y
- un análisis en el que se excluyen las variables del conjunto de variables que se están probando.
El primer modelo de regresión se llama el “modelo completo” y el segundo se llama el “modelo reducido”. La idea básica es que si el modelo reducido explica mucho menos que el modelo completo, entonces el conjunto de variables excluidas del modelo reducido es importante.
La fórmula para probar la contribución de un grupo de variables es:
\[F=\cfrac{\cfrac{SSQ_C-SSQ_R}{p_C-p_R}}{\cfrac{SSQ_T-SSQ_C}{N-p_C-1}}=\cfrac{MS_{explained}}{MS_{error}}\]
donde:
\(SSQ_C\)es la suma de cuadrados para el modelo completo,
\(SSQ_R\)es la suma de cuadrados para el modelo reducido,
\(p_C\)es el número de predictores en el modelo completo,
\(p_R\)es el número de predictores en el modelo reducido,
\(SSQ_T\)es la suma de cuadrados totales (la suma de las desviaciones cuadradas de la variable criterio a partir de su media), y
\(N\)es el número total de observaciones
Los grados de libertad para el numerador es\(p_C - p_R\) y los grados de libertad para el denominador lo son\(N - p_C -1\). Si el\(F\) es significativo, entonces se puede concluir que las variables excluidas en el conjunto reducido contribuyen a la predicción de la variable criterio independientemente de las demás variables.
Esta fórmula se puede utilizar para probar la significancia de\(R^2\) definiendo el modelo reducido como que no tiene variables predictoras. En esta aplicación,\(SSQ_R\) y\(p_R = 0\). La fórmula se simplifica de la siguiente manera:
\[F=\cfrac{\cfrac{SSQ_C}{p_C}}{\cfrac{SSQ_T-SSQ_C}{N-p_C-1}}=\cfrac{MS_{explained}}{MS_{error}}\]
que para este ejemplo se convierte en:
\[F=\cfrac{\cfrac{12.96}{2}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{6.48}{0.08}=84.35\]
Los grados de libertad son\(2\) y\(102\). La calculadora de\(F\) distribución lo demuestra\(p < 0.001\).
Calculadora F
El modelo reducido utilizado para probar la varianza explicada únicamente por un solo predictor consiste en todas las variables excepto la variable predictora en cuestión. Por ejemplo, el modelo reducido para una prueba de la contribución única de\(HSGPA\) contiene solo la variable\(SAT\). Por lo tanto, la suma de cuadrados para el modelo reducido es la suma de cuadrados cuando\(UGPA\) se predice por\(SAT\). Esta suma de cuadrados es\(9.75\). Los cálculos para\(F\) se muestran a continuación:
\[F=\cfrac{\cfrac{12.96-9.75}{2-1}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{3.212}{0.077}=41.80\]
Los grados de libertad son\(1\) y\(102\). La calculadora de\(F\) distribución lo demuestra\(p < 0.001\).
De igual manera, el modelo reducido en la prueba para la contribución única de\(SAT\) consiste en\(HSGPA\).
\[F=\cfrac{\cfrac{12.96-12.64}{2-1}}{\cfrac{20.80-12.96}{105-2-1}}=\cfrac{0.322}{0.077}=4.19\]
Los grados de libertad son\(1\) y\(102\). La calculadora de\(F\) distribución lo demuestra\(p = 0.0432\).
La prueba de significancia de la varianza explicada únicamente por una variable es idéntica a una prueba de significancia del coeficiente de regresión para esa variable. Un coeficiente de regresión y la varianza explicada de manera única por una variable reflejan la relación entre una variable y el criterio independiente de las otras variables. Si la varianza explicada de manera única por una variable no es cero, entonces el coeficiente de regresión no puede ser cero. Claramente, una variable con un coeficiente de regresión de cero explicaría ninguna varianza.
Otras estadísticas inferenciales asociadas a la regresión múltiple están fuera del alcance de este texto. Dos de particular importancia son:
- intervalos de confianza en pendientes de regresión y
- intervalos de confianza en predicciones para observaciones específicas.
Estas estadísticas inferenciales pueden ser calculadas por paquetes estándar de análisis estadístico tales como\(R\),\(SPSS\),\(STATA\),\(SAS\), y\(JMP\).
Salida SPSS Salida JMP
Supuestos
No son necesarios supuestos para calcular los coeficientes de regresión o para particionar la suma de cuadrados. Sin embargo, existen varios supuestos que se hacen al interpretar las estadísticas inferenciales. Las violaciones moderadas de los supuestos\(1-3\) no plantean un problema grave para probar la significancia de las variables predictoras. Sin embargo, incluso pequeñas violaciones de estos supuestos plantean problemas para los intervalos de confianza en las predicciones para observaciones específicas.
- Los residuos se distribuyen normalmente:
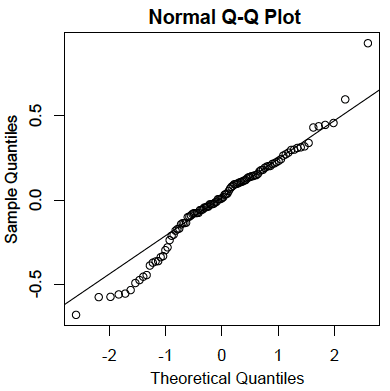
Al igual que en el caso de la regresión lineal simple, los residuales son los errores de predicción. Específicamente, son las diferencias entre los puntajes reales sobre el criterio y los puntajes pronosticados. A continuación se muestra una\(Q-Q\) gráfica para los residuos para los datos de ejemplo. Esta gráfica revela que los valores de datos reales en el extremo inferior de la distribución no aumentan tanto como se esperaría para una distribución normal. También revela que el valor más alto en los datos es mayor de lo que se esperaría para el valor más alto en una muestra de este tamaño a partir de una distribución normal. Sin embargo, la distribución no se desvía mucho de la normalidad.
- Homocedasticidad:
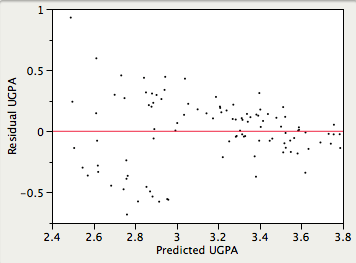
Se supone que las varianzas de los errores de predicción son las mismas para todos los valores predichos. Como se puede ver a continuación, esta suposición se viola en los datos de ejemplo porque los errores de predicción son mucho mayores para las observaciones con puntuaciones predichas bajas a medias que para las observaciones con puntuaciones predichas altas. Claramente, un intervalo de confianza en un predicho\(UGPA\) bajo subestimaría la incertidumbre.
- Linealidad:
Se supone que la relación entre cada variable predictora y la variable criterio es lineal. Si no se cumple esta suposición, entonces las predicciones pueden sobreestimar sistemáticamente los valores reales para un rango de valores en una variable predictora y subestimarlos para otro.


