Saltar al contenido principal
LibreTexts Español

14.E: Regresión (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    152336

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Preguntas Generales

    Q1

    ¿Cuál es la ecuación para una línea de regresión? ¿A qué se refiere cada término de la línea? (sección pertinente)

    Q2

    La fórmula para una ecuación de regresión basada en un tamaño de muestra de\(25\) observaciones es\(Y' = 2X + 9\).

    1. ¿Cuál sería el puntaje predicho para una persona que anota\(6\) en\(X\)?
    2. Si la puntuación predicha de alguien era\(14\), ¿cuál era la puntuación de esta persona\(X\)? (sección pertinente)

    Q3

    ¿Qué criterio se utiliza para decidir qué línea de regresión se ajusta mejor? (sección pertinente)

    Q4

    ¿Qué mide el error estándar de la estimación? ¿Cuál es la fórmula para el error estándar de la estimación? (sección pertinente)

    Q5

    1. En un análisis de regresión, la suma de cuadrados para las puntuaciones predichas es\(100\) y la suma de cuadrados es el error\(200\), ¿qué es\(R^2\)?
    2. En un análisis\(40\%\) de regresión diferente, se explicó la varianza. La suma de cuadrados totales es\(1000\). ¿Cuál es la suma de cuadrados de los valores predichos? (sección pertinente)

    Q6

    Para los\(X,Y\) datos a continuación, calcule:

    1. \(r\)y determinar si es significativamente diferente de cero.
    2. la pendiente de la línea de regresión y prueba si difiere significativamente de cero.
    3. el intervalo de\(95\%\) confianza para la pendiente.

    (sección pertinente)

    X
    Y
    2
    5
    4
    6
    4
    7
    5
    11
    6
    12

    Q7

    ¿Qué supuestos son necesarios para calcular las diversas estadísticas inferenciales de regresión lineal? (sección pertinente)

    Q8

    La correlación entre años de educación y salario en una muestra de\(20\) personas de una determinada empresa es\(0.4\). ¿Esta correlación es estadísticamente significativa a\(0.05\) nivel? (sección pertinente)

    Q9

    Se toma una muestra de\(X\) y\(Y\) puntuaciones, y se utiliza una línea de regresión para predecir a\(Y\) partir de\(X\). Si\(SSY' = 300\),\(SSE = 500\), y\(N = 50\), qué es: (sección relevante sección relevante)

    1. \(SSY\)?
    2. el error estándar de la estimación?
    3. \(R^2\)?

    Q10

    Usando regresión lineal, encuentre la puntuación predicha después de la prueba para alguien con una puntuación de\(43\) en la prueba previa. (sección pertinente)

    Pre Post
    59 56
    52 63
    44 55
    51 50
    42 66
    42 48
    41 58
    45 36
    27 13
    63 50
    54 81
    44 56
    50 64
    47 50
    55 63
    49 57
    45 73
    57 63
    46 46
    60 60
    65 47
    64 73
    50 58
    74 85
    59 44

    Q11

    La ecuación para una línea de regresión que predice el número de horas de televisión que ven los niños (\(Y\)) a partir del número de horas de televisión que ven sus padres (\(X\)) es\(Y' = 4 + 1.2X\). El tamaño de la muestra es\(12\).

    1. Si el error estándar de\(b\) es\(0.4\), ¿la pendiente es estadísticamente significativa en el\(0.05\) nivel? (sección pertinente)
    2. Si la media de\(X\) es\(8\), ¿cuál es la media de\(Y\)? (sección pertinente)

    Q12

    Con base en la siguiente tabla, calcule la línea de regresión que predice\(Y\) a partir de\(X\). (sección pertinente)

    MX
    MI
    		 sX Sy r
    10
    12
    		 2.5 3.0 -0.6

    Q13

    ¿Tiene\(A\) o\(B\) tiene un error estándar mayor de la estimación? (sección pertinente)

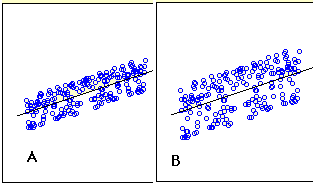
    se_est_graph.gif

    Q14

    Verdadero/falso: Si la pendiente de una línea de regresión lineal simple es estadísticamente significativa, entonces la correlación también será siempre significativa. (sección pertinente)

    Q15

    Verdadero/falso: Si la pendiente de la relación entre\(X\) y\(Y\) es\(\text{Population 1}\) mayor para que para\(\text{Population 2}\), la correlación necesariamente será\(\text{Population 1}\) mayor en que en\(\text{Population 1}\). ¿Por qué o por qué no? (sección pertinente)

    Q16

    Verdadero/falso: Si la correlación es\(0.8\), entonces se explica\(40\%\) de la varianza. (sección pertinente)

    Q17

    Verdadero/falso: Si la\(Y\) puntuación real fue\(31\), pero la puntuación predicha fue\(28\), entonces el error de predicción es\(3\). (sección pertinente)

    Preguntas de casos prácticos

    La siguiente pregunta es del estudio de caso Angry Moods (AM).

    Q18

    (AM #23) Encuentra la línea de regresión para predecir Anger-Out a partir de Control-Out.

    1. ¿Cuál es la pendiente?
    2. ¿Cuál es la interceptación?
    3. ¿La relación es al menos aproximadamente lineal?
    4. Prueba para ver si la pendiente es significativamente diferente de\(0\).
    5. ¿Cuál es el error estándar de la estimación?

    (sección pertinente, sección pertinente, sección pertinente)

    La siguiente pregunta es del estudio de caso SAT y GPA (SG).

    Q19

    (SG #3) Encuentra la línea de regresión para predecir el GPA general universitario a partir del GPA de secundaria.

    1. ¿Cuál es la pendiente?
    2. ¿Qué es la\(y\) -intercepción?
    3. Si alguien tuvo un\(2.2\) GPA en la preparatoria, ¿cuál es la mejor estimación de su GPA universitario?
    4. Si alguien tuvo un\(4.0\) GPA en la preparatoria, ¿cuál es la mejor estimación de su GPA universitario?

    (sección pertinente)

    Las siguientes preguntas son del estudio de caso Driving (D).

    Q20

    (D #5) ¿Cuál es la correlación entre la edad y la frecuencia con la que la persona elige conducir en condiciones climáticas adversas? ¿Esta correlación es estadísticamente significativa a\(0.01\) nivel? ¿Las personas mayores son más o menos propensas a informar que conducen en condiciones climáticas adversas? (sección pertinente, sección pertinente)

    Q21

    (D #8) ¿Cuál es la correlación entre la frecuencia con la que una persona elige conducir en condiciones climáticas adversas y el porcentaje de accidentes que la persona cree que ocurren en condiciones climáticas adversas? ¿Esta correlación es significativamente diferente de\(0\)? (sección pertinente, sección pertinente)

    Q22

    (D #10) Utilice la regresión lineal para predecir la frecuencia con la que alguien monta el transporte público en condiciones climáticas adversas a partir del porcentaje de accidentes que esa persona piensa que ocurren en las inclemencias del tiempo. (Pubtran por Accidente)

    1. Cree una gráfica de dispersión de estos datos y agregue una línea de regresión.
    2. ¿Cuál es la pendiente?
    3. ¿Cuál es la interceptación?
    4. ¿La relación es al menos aproximadamente lineal?
    5. Pruebe si la pendiente es significativamente diferente de\(0\).
    6. Comentar posibles violaciones de suposición para la prueba de la pendiente.
    7. ¿Cuál es el error estándar de la estimación?

    (sección pertinente, sección pertinente, sección pertinente)

    Respuestas Seleccionadas

    S2

    1. \(21\)

    S5

    1. \(0.33\)

    S6

    1. \(b = 1.91\)

    S9

    1. \(800\)

    S12

    \(a = 19.2\)

    S18

    1. \(3.45\)

    S19

    1. \(2.6\)

    S20

    \(r = 0.43\)

    S22

    1. \(0.35\)

    This page titled 14.E: Regresión (Ejercicios) is shared under a Public Domain license and was authored, remixed, and/or curated by David Lane via source content that was edited to the style and standards of the LibreTexts platform.