15.3: ANOVA de un factor
- Page ID
- 152291
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Declarar lo que estima el Cuadrado Medio Entre (\(MSB\)) cuando la hipótesis nula es verdadera y cuando la hipótesis nula es falsa
- Compute\(MSE\)
- Computación\(F\) y sus parámetros de dos grados de libertad
- Explique por qué el ANOVA se considera mejor como una prueba de dos colas aunque literalmente solo se usa una cola de la distribución
- Divide las sumas de cuadrados en condición y error
- Dar formato a los datos para ser utilizados con un programa de estadísticas informáticas
En esta sección se muestra cómo se puede utilizar el ANOVA para analizar un diseño de un factor entre sujetos. Utilizaremos como ejemplo principal el estudio de caso “Sonrisas y clemencia”. En este estudio hubo cuatro condiciones con\(34\) sujetos en cada condición. Hubo una puntuación por materia. La hipótesis nula probada por ANOVA es que las medias poblacionales para todas las condiciones son las mismas. Esto se puede expresar de la siguiente manera:
\[H_0: \mu _1 = \mu _2 = ... = \mu _k\]
donde\(H_0\) está la hipótesis nula y\(k\) es el número de condiciones. En el estudio “Sonrisas y clemencia”,\(k = 4\) y la hipótesis nula es
\[H_0: \mu _{false} = \mu _{felt} = \mu _{miserable} = \mu _{neutral}\]
Si se rechaza la hipótesis nula, entonces se puede concluir que al menos una de las medias poblacionales es diferente de al menos otra media poblacional.
El análisis de varianza es un método para probar diferencias entre medias mediante el análisis de varianza. La prueba se basa en dos estimaciones de la varianza poblacional (\(\sigma ^2\)). Una estimación se llama error cuadrático medio (\(MSE\)) y se basa en diferencias entre puntuaciones dentro de los grupos. \(MSE\)estima\(\sigma ^2\) independientemente de si la hipótesis nula es verdadera (las medias poblacionales son iguales). La segunda estimación se llama el cuadrado medio entre (\(MSB\)) y se basa en diferencias entre las medias de la muestra. \(MSB\)sólo estima\(\sigma ^2\) si las medias poblacionales son iguales. Si las medias poblacionales no son iguales, entonces\(MSB\) estima una cantidad mayor que\(\sigma ^2\). Por lo tanto, si el\(MSB\) es mucho mayor que el\(MSE\), entonces es poco probable que las medias poblacionales sean iguales. Por otro lado, si el\(MSB\) es aproximadamente lo mismo que\(MSE\), entonces los datos son consistentes con la hipótesis nula de que las medias poblacionales son iguales.
Antes de proceder al cálculo de\(MSE\) y\(MSB\), es importante considerar los supuestos hechos por ANOVA:
- Las poblaciones tienen la misma varianza. Esta suposición se llama la suposición de\(\textit{homogeneity of variance}\).
- Las poblaciones se distribuyen normalmente.
- Cada valor se muestrea independientemente uno del otro valor. Esta suposición requiere que cada sujeto proporcione un solo valor. Si un sujeto proporciona dos puntuaciones, entonces los valores no son independientes. El análisis de datos con dos puntuaciones por materia se muestra en el apartado sobre ANOVA dentro de los sujetos más adelante en este capítulo.
Estos supuestos son los mismos que para una prueba t de diferencias entre grupos salvo que se aplican a dos o más grupos, no sólo a dos grupos.
Las medias y varianzas de los cuatro grupos en el estudio de caso “Sonrisas y clemencia” se muestran en la Tabla\(\PageIndex{1}\). Obsérvese que hay\(34\) sujetos en cada una de las cuatro condiciones (Falso, Sentido, Miserable y Neutral).
| Condición | Media | Varianza |
|---|---|---|
| Falso | 5.3676 | 3.3380 |
| Fieltro | 4.9118 | 2.8253 |
| Miserable | 4.9118 | 2.1132 |
| Neutral | 4.1176 | 2.3191 |
Tamaños de Muestras
Todos los primeros cálculos de esta sección asumen que hay un número igual de observaciones en cada grupo. Aquí se muestran cálculos desiguales de tamaño de muestra. Nos referiremos al número de observaciones en cada grupo como\(n\) y al número total de observaciones como\(N\). Para estos datos hay cuatro grupos de\(34\) observaciones. Por lo tanto,\(n = 34\) y\(N = 136\).
Computación MSE
Recordemos que el supuesto de homogeneidad de varianza establece que la varianza dentro de cada una de las poblaciones (\(\sigma ^2\)) es la misma. Esta varianza,\(\sigma ^2\), es la cantidad estimada por\(MSE\) y se calcula como la media de las varianzas de la muestra. Para estos datos, el\(MSE\) es igual a\(2.6489\).
Computación MSB
La fórmula para\(MSB\) se basa en el hecho de que la varianza de la distribución muestral de la media es
\[\sigma _{M}^{2}=\frac{\sigma ^2}{n}\]
donde\(n\) está el tamaño muestral de cada grupo. Reordenando esta fórmula, tenemos
\[\sigma ^2=n\sigma _{M}^{2}\]
Por lo tanto, si conociéramos la varianza de la distribución muestral de la media, podríamos\(\sigma ^2\) calcularla multiplicándola por\(n\). Aunque no conocemos la varianza de la distribución muestral de la media, podemos estimarla con la varianza de las medias de la muestra. Para los datos de clemencia, la varianza de las cuatro medias muestrales es\(0.270\). Para estimar\(\sigma ^2\), multiplicamos la varianza de las medias muestrales (\(0.270\)) por\(n\) (el número de observaciones en cada grupo, que es\(34\)). Nos encontramos con eso\(MSB = 9.179\).
Para resumir estos pasos:
- Compute los medios.
- Computar la varianza de las medias.
- Multiplique la varianza de las medias por\(n\).
Recapitulación
Si las medias poblacionales son iguales, entonces ambas\(MSE\) y\(MSB\) son estimaciones de\(\sigma ^2\) y, por lo tanto, deberían ser aproximadamente las mismas. Naturalmente, no serán exactamente los mismos ya que son solo estimaciones y se basan en diferentes aspectos de los datos: El\(MSB\) se calcula a partir de las medias de la muestra y el\(MSE\) se calcula a partir de las varianzas de la muestra.
Si las medias poblacionales no son iguales, entonces aún\(MSE\) se estimará\(\sigma ^2\) porque las diferencias en las medias poblacionales no afectan las varianzas. Sin embargo, las diferencias en las medias poblacionales afectan\(MSB\) ya que las diferencias entre medias poblacionales se asocian con diferencias entre medias de la muestra De ello se deduce que cuanto mayores sean las diferencias entre las medias de la muestra, mayor será la\(MSB\).
Nota
En definitiva,\(MSE\) estima\(\sigma ^2\) si las medias poblacionales son iguales o no, mientras que las\(MSB\) estimaciones\(\sigma ^2\) sólo cuando las medias poblacionales son iguales y estima una cantidad mayor cuando no son iguales.
Comparando MSE y MSB
El paso crítico en un ANOVA es comparar\(MSE\) y\(MSB\). Dado que\(MSB\) estima una cantidad mayor que\(MSE\) sólo cuando las medias poblacionales no son iguales, un hallazgo de una\(MSB\) mayor que una\(MSE\) es una señal de que las medias poblacionales no son iguales. Pero como\(MSB\) podría ser mayor que\(MSE\) por casualidad aunque los medios poblacionales sean iguales,\(MSB\) debe ser mucho mayor que\(MSE\) para justificar la conclusión de que los medios poblacionales difieren. Pero, ¿cuánto más grande debe\(MSB\) ser? Para los datos de “Sonrisas y clemencia”, los\(MSB\) y\(MSE\) son\(9.179\) y\(2.649\), respectivamente. ¿Esa diferencia es lo suficientemente grande? Para responder, necesitaríamos saber la probabilidad de obtener una diferencia tan grande o una diferencia mayor si las medias de la población fueran todas iguales. Las matemáticas necesarias para responder a esta pregunta fueron elaboradas por el estadístico R. Fisher. Aunque la formulación original de Fisher tomó una forma ligeramente diferente, el método estándar para determinar la probabilidad se basa en la relación de\(MSB\) a\(MSE\). Esta relación lleva el nombre de Fisher y se llama la\(F\) relación.
Para estos datos, la\(F\) relación es
\[F = \frac{9.179}{2.649} = 3.465\]
Por lo tanto, el\(MSB\) es\(3.465\) veces mayor que\(MSE\). ¿Esto hubiera sido probable que ocurriera si todos los medios de la población fueran iguales? Eso depende del tamaño de la muestra. Con un tamaño de muestra pequeño, no sería demasiado sorprendente porque los resultados de muestras pequeñas son inestables. Sin embargo, con una muestra muy grande, los\(MSB\) y\(MSE\) son casi siempre aproximadamente los mismos, y una\(F\) proporción de\(3.465\) o mayor sería muy inusual. La figura\(\PageIndex{1}\) muestra la distribución muestral del\(F\) tamaño muestral en el estudio “Sonrisas y clemencia”. Como puede ver, tiene un sesgo positivo.
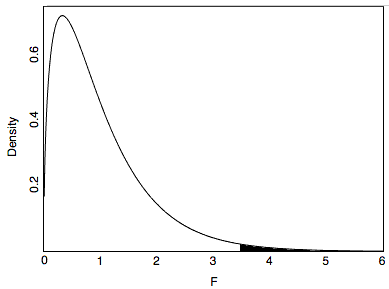
De la Figura\(\PageIndex{1}\), se puede ver que\(F\) las proporciones de\(3.465\) o por encima son ocurrencias inusuales. El área a la derecha de\(3.465\) representa la probabilidad de un\(F\) que grande o más grande y es igual a\(0.018\). Es decir, dada la hipótesis nula de que todas las medias poblacionales son iguales, el valor de probabilidad es\(0.018\) y por lo tanto la hipótesis nula puede ser rechazada. Se justifica la conclusión de que al menos uno de los medios de la población es diferente de al menos uno de los otros.
La forma de la\(F\) distribución depende del tamaño de la muestra. Más precisamente, depende de dos grados de libertad (\(df\)) parámetros: uno para el numerador (\(MSB\)) y otro para el denominador (\(MSE\)). Recordemos que los grados de libertad para una estimación de varianza es igual al número de observaciones menos uno. Ya que el\(MSB\) es la varianza de\(k\) medios, tiene\(k - 1\)\(df\). El\(MSE\) es un promedio de\(k\) varianzas, cada una con\(n - 1\)\(df\). Por lo tanto, el\(df\) for\(MSE\) es\(k(n - 1) = N - k\), donde\(N\) está el número total de observaciones,\(n\) es el número de observaciones en cada grupo, y\(k\) es el número de grupos. Para resumir:
\[df_{numerator} = k-1\]
\[df_{denominator} = N-k\]
Para los datos de “Sonrisas y clemencia”
\[df_{numerator} = k-1=4-1=3\]
\[df_{denominator} = N-k=136-4=132\]
\(F = 3.465\)
La calculadora de\(F\) distribución lo demuestra\(p = 0.018\).
Calculadora F
¿Una Cola o Dos?
¿El valor de probabilidad de una\(F\) relación es una probabilidad de una cola o una de dos colas? En el sentido literal, se trata de una probabilidad de una cola ya que, como se puede ver en la Figura\(\PageIndex{1}\), la probabilidad es el área en la cola derecha de la distribución. Sin embargo, la\(F\) relación es sensible a cualquier patrón de diferencias entre medias. Es, por lo tanto, una prueba de una hipótesis de dos colas y se considera mejor una prueba de dos colas.
Relación con la\(t\) prueba
Dado que un ANOVA y una\(t\) prueba de grupos independientes pueden probar la diferencia entre dos medias, tal vez se esté preguntando cuál usar. Afortunadamente, no importa ya que los resultados siempre serán los mismos. Cuando sólo hay dos grupos, la siguiente relación entre\(F\) y siempre\(t\) se mantendrá:
\[F(1,dfd) = t^2(df)\]
donde están\(dfd\) los grados de libertad para el denominador de la\(F\) prueba y\(df\) son los grados de libertad para la\(t\) prueba. \(dfd\)siempre será igual\(df\).
Fuentes de Variación
¿Por qué las puntuaciones en un experimento difieren entre sí? Considere las puntuaciones de dos sujetos en el estudio “Sonrisas y clemencia”: uno de la condición “Sonrisa falsa” y otro de la condición “Sonrisa de fieltro”. Una posible razón obvia por la que los puntajes podrían diferir es que los sujetos fueron tratados de manera diferente (estaban en diferentes condiciones y vieron diferentes estímulos). Una segunda razón es que los dos sujetos pueden haber diferido en cuanto a su tendencia a juzgar a las personas con indulgencia. Un tercero es que, tal vez, uno de los sujetos estaba de mal humor después de recibir una nota baja en una prueba. Se puede imaginar que hay otras innumerables razones por las que las puntuaciones de las dos asignaturas podrían diferir. Todas estas razones excepto la primera (los sujetos fueron tratados de manera diferente) son posibilidades que no estaban bajo investigación experimental y, por lo tanto, todas las diferencias (variación) debidas a estas posibilidades son inexplicables. Es tradicional llamar error de varianza inexplicable a pesar de que no hay implicación de que se cometió un error. Por lo tanto, se puede pensar que la variación en este experimento es variación por la condición en la que se encontraba el sujeto o por error (la suma total de todas las razones por las que las puntuaciones de los sujetos podrían diferir que no se midieron).
Una de las características importantes del ANOVA es que divide la variación en sus diversas fuentes. En ANOVA, se utiliza el término suma de cuadrados (\(SSQ\)) para indicar variación. La variación total se define como la suma de las diferencias cuadradas entre cada puntaje y la media de todos los sujetos. La media de todos los sujetos se llama la gran media y se designa como GM. (Cuando hay un número igual de sujetos en cada condición, la gran media es la media de las medias de condición). La suma total de cuadrados se define como
\[SSQ_{total}=\sum (X-GM)^2\]
lo que significa tomar cada puntaje, restarle la gran media, cuadrar la diferencia y luego resumir estos valores al cuadrado. Para el estudio “Sonrisas y clemencia”,\(SSQ_{total}=377.19\).
La condición de suma de cuadrados se calcula como se muestra a continuación.
\[SSQ_{condition}=n\left [ (M_1-GM)^2 + (M_2-GM)^2 + \cdots +(M_k-GM)^2 \right ]\]
donde\(n\) es el número de puntuaciones en cada grupo,\(k\) es el número de grupos,\(M_1\) es la media para\(\text{Condition 1}\),\(M_2\) es la media para\(\text{Condition 2}\), y\(M_k\) es la media para\(\text{Condition k}\). Para el estudio Sonrisas y Leniencia, los valores son:
\[\begin{align*} SSQ_{condition} &= 34\left [ (5.37-4.83)^2 + (4.91-4.83)^2 + (4.91-4.83)^2 + (4.12-4.83)^2\right ]\\ &= 27.5 \end{align*}\]
Si hay tamaños de muestra desiguales, el único cambio es que se utiliza la siguiente fórmula para la condición de suma de cuadrados:
\[SSQ_{condition}=n_1(M_1-GM)^2 + n_2(M_2-GM)^2 + \cdots + n_k(M_k-GM)^2\]
donde\(n_i\) está el tamaño de la muestra de la\(i^{th}\) condición. \(SSQ_{total}\)se calcula de la misma manera que se muestra arriba.
El error de suma de cuadrados es la suma de las desviaciones cuadradas de cada puntaje de su media grupal. Esto se puede escribir como
\[SSQ_{error}=\sum (X_{i1}-M_1)^2 + \sum (X_{i2}-M_2)^2 + \cdots + \sum (X_{ik}-M_k)^2\]
donde\(X_{i1}\) está la\(i^{th}\) puntuación en\(\text{group 1}\) y\(M_1\) es la media para\(\text{group 1}\),\(X_{i2}\) es la\(i^{th}\) puntuación en\(\text{group 2}\) y\(M_2\) es la media para\(\text{group 2}\), etc. Para el estudio “Sonrisas y clemencia”, las medias son:\(5.368\),\(4.912\),\(4.912\), y \(4.118\). El\(SSQ_{error}\) es por lo tanto:
\[\begin{align*} SSQ_{error} &= (2.5-5.368)^2 + (5.5-5.368)^2 + ... + (6.5-4.118)^2\\ &= 349.65 \end{align*}\]
La suma del error de cuadrados también se puede calcular por resta:
\[SSQ_{error} = SSQ_{total} - SSQ_{condition}\]
\[\begin{align*} SSQ_{error} &= 377.189 - 27.535\\ &= 349.65 \end{align*}\]
Por lo tanto, la suma total de cuadrados de se\(377.19\) puede dividir en\(SSQ_{condition}(27.53)\) y\(SSQ_{error} (349.66)\).
Una vez que se han calculado las sumas de cuadrados, los cuadrados medios (\(MSB\)y\(MSE\)) se pueden calcular fácilmente. Las fórmulas son:
\[MSB = \frac{SSQ_{condition}}{dfn}\]
donde\(dfn\) está el numerador grados de libertad y es igual a\(k - 1 = 3\).
\[MSB = \frac{27.535}{3}=9.18\]
que es el mismo valor\(MSB\) obtenido previamente (salvo error de redondeo). Del mismo modo,
\[MSE = \frac{SSQ_{error}}{dfd}\]
donde están\(dfd\) los grados de libertad para el denominador y es igual a\(N - k\).
\(dfd = 136 - 4 = 132\)
\(MSE = 349.66/132 = 2.65\)
que es lo mismo que se obtuvo anteriormente (excepto por error de redondeo). Tenga en cuenta que el\(dfd\) suele llamarse\(dfe\) el error de grados de libertad.
La Tabla Resumen de Análisis de Varianza que se muestra a continuación es una forma conveniente de resumir la partición de la varianza. Se han corregido los errores de redondeo.
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Condición | 3 | 27.5349 | 9.1783 | 3.465 | 0.0182 |
| Error | 132 | 349.6544 | 2.6489 | ||
| Total | 135 | 377.1893 |
La primera columna muestra las fuentes de variación, la segunda columna muestra los grados de libertad, la tercera muestra las sumas de cuadrados, la cuarta muestra los cuadrados medios, la quinta muestra la\(F\) relación y la última muestra el valor de probabilidad. Tenga en cuenta que los cuadrados medios son siempre las sumas de cuadrados divididos por grados de libertad. Los\(F\) y\(p\) son relevantes solo para la Condición. Si bien el total cuadrático medio podría calcularse dividiendo la suma de cuadrados por los grados de libertad, generalmente no es de mucho interés y se omite aquí.
Formateo de Datos para Análisis por Computadora
La mayoría de los programas informáticos que calculan ANOVA requieren que sus datos estén en una forma específica. Considera los datos en la Tabla\(\PageIndex{3}\).
| Grupo 1 | Grupo 2 | Grupo 3 |
|---|---|---|
| 3 | 2 | 8 |
| 4 | 4 | 5 |
| 5 | 6 | 5 |
Aquí hay tres grupos, cada uno con tres observaciones. Para formatear estos datos para un programa de computadora, normalmente hay que usar dos variables: la primera especifica el grupo en el que se encuentra el sujeto y la segunda es la propia puntuación. La versión reformateada de los datos en la Tabla\(\PageIndex{3}\) se muestra en la Tabla\(\PageIndex{4}\).
| G | Y |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 2 | 2 |
| 2 | 4 |
| 2 | 6 |
| 3 | 8 |
| 3 | 5 |
| 3 | 5 |
Para usar Analysis Lab para hacer los cálculos, copiaría los datos y luego
- Haga clic en el botón “Ingresar/Editar datos”. (Es posible que se le avise que por razones de seguridad debe usar el método abreviado de teclado para pegar datos).
- Pegue sus datos.
- Haga clic en “Aceptar datos”.
- Establezca la variable dependiente en\(Y\).
- Establezca la variable de agrupación en\(G\).
- Haga clic en el botón ANOVA.
Encontrarás eso\(F = 1.5\) y\(p = 0.296\).


