19.4: Explicación de la proporción de varianza
- Page ID
- 152420
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Anotar la diferencia de sesgo entre\(η^2\) y\(ω^2\)
- \(η^2\)Cómputos\(ω^2\)
- Distinguir entre\(ω^2\) y parcial\(ω^2\)
- Exponer el sesgo\(R^2\) y qué se puede hacer para reducirlo
Los tamaños de los efectos a menudo se miden en términos de la proporción de varianza explicada por una variable. En esta sección se discute esta manera de medir el tamaño del efecto tanto en diseños de ANOVA como en estudios correlacionales.
Diseños ANOVA
Las respuestas de los sujetos variarán en casi cada experimento. Consideremos, por ejemplo, el estudio de caso “Sonrisas y clemencia”. En la Figura se muestra un histograma de la variable dependiente “cleniencia”\(\PageIndex{1}\). Es claro que los puntajes de clemencia varían considerablemente. Hay muchas razones por las que los puntajes difieren. Una, por supuesto, es que los sujetos fueron asignados a cuatro condiciones diferentes de sonrisa y la condición en la que se encontraban pudo haber afectado su puntaje de clemencia. Además, es probable que algunos sujetos sean generalmente más indulgentes que otros, contribuyendo así a las diferencias entre los puntajes. Hay muchas otras posibles fuentes de diferencias en las calificaciones de clemencia incluyendo, quizás, que algunos sujetos estaban en mejores estados de ánimo que otros sujetos y/o que algunos sujetos reaccionaron más negativamente que otros a las miradas o manierismos de la persona de estímulo. Se puede imaginar que hay innumerables otras razones por las que los puntajes de los sujetos podrían diferir.
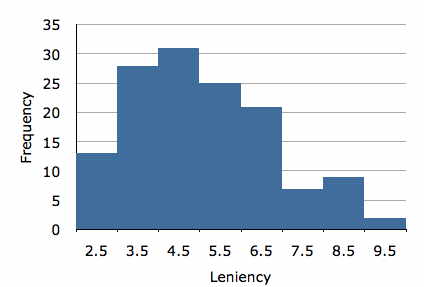
Una manera de medir el efecto de las condiciones es determinar la proporción de la varianza entre los puntajes de los sujetos que es atribuible a las condiciones. En este ejemplo, la varianza de puntuaciones es\(2.794\). La pregunta es cómo se compara esta varianza con cuál habría sido la varianza si cada sujeto hubiera estado en la misma condición de tratamiento. Estimamos esto calculando la varianza dentro de cada una de las condiciones de tratamiento y tomando la media de estas varianzas. Para este ejemplo, la media de las varianzas es\(2.649\). Dado que la varianza media dentro de las condiciones de sonrisa no es mucho menor que la varianza ignorando las condiciones, es claro que “Condición de Sonrisa” no es responsable de un alto porcentaje de la varianza de las puntuaciones. La forma más conveniente de calcular la proporción explicada es en términos de la suma de cuadrados “condiciones” y la suma de cuadrados totales. Los cálculos para estas sumas de cuadrados se muestran en el capítulo sobre ANOVA. Para los presentes datos, la suma de cuadrados para “Condición de Sonrisa” es\(27.535\) y la suma de cuadrados total es\(377.189\). Por lo tanto, la proporción explicada por “Condición de Sonrisa” es:
\[\frac{27.535}{377.189} = 0.073\]
Así,\(0.073\) o\(7.3\%\) de la varianza se explica por “Condición de Sonrisa”.
Una forma alternativa de ver la varianza explicada es como la reducción de proporción en el error. La suma de cuadrados total (\(377.189\)) representa la variación cuando se ignora “Condición de Sonrisa” y la suma de cuadrados error (\(377.189 - 27.535 = 349.654\)) es la variación sobrante cuando se contabiliza “Condición de Sonrisa”. La diferencia entre\(377.189\) y\(349.654\) es\(27.535\). Esta reducción en el error de\(27.535\) representa una reducción proporcional de\(27.535/377.189 = 0.073\), el mismo valor calculado en términos de proporción de varianza explicado.
Esta medida del tamaño del efecto, ya sea computada en términos de varianza explicada o en términos de reducción porcentual en el error, se denomina\(η^2\) donde\(η\) se encuentra la letra griega eta. Desafortunadamente,\(η^2\) tiende a sobreestimar la varianza explicada y por lo tanto es una estimación sesgada de la proporción de varianza explicada. Como tal, no se recomienda (a pesar de que es reportado por un paquete estadístico líder).
Una medida alternativa,\(ω^2\) (omega al cuadrado), es imparcial y puede calcularse a partir de
\[\omega ^2 = \frac{SSQ_{condition}-(k-1)MSE}{SSQ_{total}+MSE}\]
donde\(MSE\) está el error cuadrático medio y\(k\) es el número de condiciones. Para este ejemplo,\(k = 4\) y\(ω^2 = 0.052\).
Es importante tener en cuenta que tanto la variabilidad de la población muestreada como los niveles específicos de la variable independiente son determinantes importantes de la proporción de varianza explicada. Considerar dos posibles diseños de un experimento que investigue el efecto del consumo de alcohol en la capacidad de conducción. Como se puede observar en la Tabla\(\PageIndex{1}\),\(\text{Design 1}\) tiene un rango de dosis menor y una población más diversa que\(\text{Design 2}\). ¿Cuáles son las implicaciones para la proporción de varianza explicada por Dosis? La variación debida a la Dosis sería\(\text{Design 2}\) mayor en que\(\text{Design 1}\) ya que el alcohol se manipula con mayor fuerza que en\(\text{Design 1}\). Sin embargo, la varianza en la población debería ser mayor\(\text{Design 1}\) ya que incluye un conjunto más diverso de conductores. Dado que con\(\text{Design 1}\) la varianza por Dosis sería menor y la varianza total sería mayor, la proporción de varianza explicada por Dosis sería mucho\(\text{Design 1}\) menor usando que usando\(\text{Design 2}\). Así, la proporción de varianza explicada no es una característica general de la variable independiente. En cambio, depende de los niveles específicos de la variable independiente utilizada en el experimento y de la variabilidad de la población muestreada.
|
Diseño |
Dosis |
Población |
|
1 |
0.00 |
Todos los Conductores entre 16 y 80 Años de Edad |
|
0.30 |
||
|
0.60 |
||
|
2 |
0.00 |
Conductores experimentados entre 25 y 30 años de edad |
|
0.50 |
||
|
1.00 |
Diseños factoriales
En los diseños de un factor, la suma de cuadrados totales es la condición de suma de cuadrados más la suma de cuadrados de error. La proporción de varianza explicada se define relativa a la suma de cuadrados totales. En un\(A \times B\) diseño, hay tres fuentes de variación (\(A, B, A \times B\)) además del error. La proporción de varianza explicada para una variable (\(A\), por ejemplo) podría definirse relativa a la suma de cuadrados total (\(SSQ_A + SSQ_B + SSQ_{A\times B} + SSQ_{error}\)) o relativa a\(SSQ_A + SSQ_{error}\).
Para ilustrar con un ejemplo, considere un experimento hipotético sobre los efectos de la edad (\(6\)y\(12\) años) y de los métodos de enseñanza de la lectura (condiciones experimentales y de control). Las medias se muestran en la Tabla\(\PageIndex{2}\). La desviación estándar de cada una de las cuatro celdas (\(Age \times Treatment\)combinaciones) es\(5\). (Naturalmente, para datos reales, las desviaciones estándar no serían exactamente iguales y las medias no serían números enteros.) Finalmente, hubo\(10\) sujetos por célula dando como resultado un total de\(40\) sujetos.
| Tratamiento | ||
|---|---|---|
| Edad | Experimental | Control |
| 6 | 40 | 42 |
| 12 | 50 | 56 |
Las fuentes de variación, los grados de libertad y las sumas de cuadrados del cuadro resumen de análisis de varianza, así como cuatro medidas del tamaño del efecto se muestran en la Tabla\(\PageIndex{3}\). Obsérvese que la suma de cuadrados para la edad es muy grande en relación con los otros dos efectos. Esto es lo que se esperaría ya que la diferencia en la capacidad lectora entre los niños de\(6\) - y\(12\) -años es muy grande en relación con el efecto de la condición.
| Fuente | df | SSQ | \(η^2\) | parcial \(η^2\) |
\(ω^2\) | parcial \(ω^2\) |
|---|---|---|---|---|---|---|
| Edad | 1 | 1440 | \ (η^2\) ">0.567 | \ (η^2\) ">0.615 | \ (ω^2\) ">0.552 | \ (ω^2\) ">0.586 |
| Condición | 1 | 160 | \ (η^2\) ">0.063 | \ (η^2\) ">0.151 | \ (ω^2\) ">0.053 | \ (ω^2\) ">0.119 |
| A x C | 1 | 40 | \ (η^2\) ">0.016 | \ (η^2\) ">0.043 | \ (ω^2\) ">0.006 | \ (ω^2\) ">0.015 |
| Error | 36 | 900 | ||||
| Total | 39 | 2540 |
Primero, consideramos los dos métodos de computación\(η^2\), etiquetados\(η^2\) y parciales\(η^2\). El valor de\(η^2\) para un efecto es simplemente la suma de cuadrados para este efecto dividida por la suma de cuadrados totales. Por ejemplo, el\(η^2\) para la Edad es\(1440/2540 = 0.567\). Al igual que en un diseño de un factor,\(η^2\) es la proporción de la variación total explicada por una variable. Parcial\(η^2\) para Edad se\(SSQ_{Age}\) divide por (\(SSQ_{Age} + SSQ_{error}\)), que es\(1440/2340 = 0.615\).
Como puede ver, el parcial\(η^2\) es mayor que\(η^2\). Esto se debe a que el denominador es menor para el parcial\(η^2\). La diferencia entre\(η^2\) y parcial\(η^2\) es aún mayor por el efecto de la condición. Esto se debe a que\(SSQ_{Age}\) es grande y hace una gran diferencia esté o no incluido en el denominador.
Como se señaló anteriormente, es mejor usar\(ω^2\) que\(η^2\) porque\(η^2\) tiene un sesgo positivo. Se puede ver que los valores para\(ω^2\) son menores que para\(η^2\). Los cálculos para\(ω^2\) se muestran a continuación:
\[\omega ^2 = \frac{SSQ_{effect}-df_{effect}MS_{error}}{SSQ_{total}+MS_{error}}\]
\[\omega _{partial}^2 = \frac{SSQ_{effect}-df_{effect}MS_{error}}{SSQ_{effect}+(N-df_{effect})MS_{error}}\]
donde\(N\) es el número total de observaciones.
La elección de si usar\(ω^2\) o lo parcial\(ω^2\) es subjetiva; ninguno es correcto ni incorrecto. No obstante, es importante entender la diferencia y, si estás usando software de computadora, saber qué versión se está calculando. (Cuidado, al menos un paquete de software etiqueta las estadísticas incorrectamente).
Estudios Correlacionales
En la sección “Particionar las sumas de cuadrados” del capítulo Regresión, vimos que la suma de cuadrados para\(Y\) (la variable criterio) se puede dividir en la suma de cuadrados explicada y el error de la suma de cuadrados. Por lo tanto, la proporción de varianza explicada en la regresión múltiple es:
\[SSQ_{explained}/SSQ_{total }\]
En regresión simple, la proporción de varianza explicada es igual a\(r^2\); en regresión múltiple, es igual a\(R^2\).
En general,\(R^2\) es análogo\(η^2\) y es una estimación sesgada de la varianza explicada. La siguiente fórmula para ajustado\(R^2\) es análoga a\(ω^2\) y es menos sesgada (aunque no completamente imparcial):
\[R_{adjusted}^{2} = 1 - \frac{(1-R^2)(N-1)}{N-p-1}\]
donde\(N\) es el número total de observaciones y\(p\) es el número de variables predictoras.


