8.2: Pruebas de muestra grande para una media poblacional
- Page ID
- 151147
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Aprender a aplicar el procedimiento de prueba de cinco pasos para una prueba de hipótesis sobre una media poblacional cuando el tamaño de la muestra es grande.
- Aprender a interpretar el resultado de una prueba de hipótesis en el contexto de la situación narrada original.
En esta sección describimos y demostramos el procedimiento para realizar una prueba de hipótesis sobre la media de una población en el caso de que el tamaño de la muestra\(n\) sea al menos\(30\). El Teorema del Límite Central establece que\(\overline{X}\) se distribuye aproximadamente normalmente, y tiene media\(\mu _{\overline{X}}=\mu\) y desviación estándar\(\sigma _{\overline{X}}=\sigma /\sqrt{n}\), donde\(\mu\) y\(\sigma\) son la media y la desviación estándar de la población. Esto implica que la estadística
\[\frac{\bar{x}-\mu }{\sigma /\sqrt{n}}\]
tiene la distribución normal estándar, lo que significa que las probabilidades relacionadas con ella se dan en la Figura 7.1.5 y la última línea en la Figura 7.1.6.
Si sabemos\(\sigma\) entonces la estadística en la pantalla es nuestra estadística de prueba. Si, como suele ser el caso, no lo sabemos\(\sigma\), entonces lo reemplazamos por la desviación estándar de la muestra\(s\). Dado que la muestra es grande el estadístico de prueba resultante todavía tiene una distribución que es aproximadamente normal estándar.
Estadísticas de pruebas estandarizadas para pruebas de hipótesis de muestra grande en relación con una media poblacional
- Si\(\sigma\) se conoce:\(Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}\)
- Si\(\sigma\) se desconoce:\(Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\)
El estadístico de prueba tiene la distribución normal estándar.
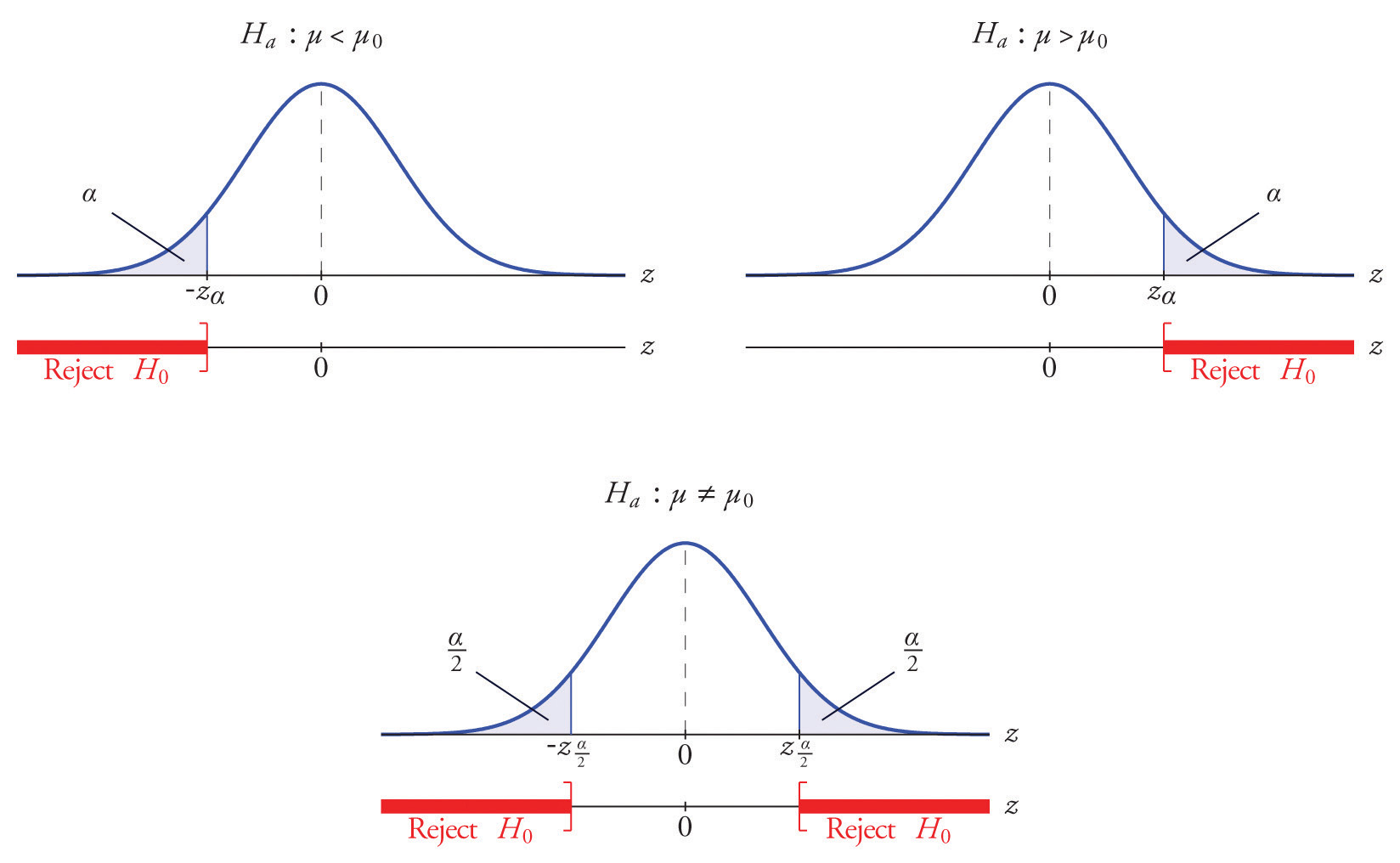
La distribución del estadístico de prueba estandarizado y la región de rechazo correspondiente para cada forma de hipótesis alternativa (cola izquierda, cola derecha o dos colas), se muestra en la Figura\(\PageIndex{1}\).
Ejemplo\(\PageIndex{1}\)
Se espera que un analgésico recién desarrollado produzca más rápidamente una reducción perceptible del dolor en los pacientes después de cirugías menores que un analgésico estándar. Se sabe que el analgésico estándar aporta alivio en un promedio de\(3.5\) minutos con minutos de desviación\(2.1\) estándar. Para probar si el nuevo analgésico funciona más rápido que el estándar, a\(50\) los pacientes con cirugías menores se les dio el nuevo analgésico y se registraron sus tiempos de alivio. El experimento arrojó\(\bar{x}=3.1\) minutos medios de muestra y minutos de desviación\(s=1.5\) estándar de la muestra. ¿Hay evidencia suficiente en la muestra para indicar, a\(5\%\) nivel de significancia, que el analgésico recién desarrollado entrega un alivio perceptible más rápidamente?
Solución:
Realizamos la prueba de hipótesis utilizando el procedimiento de cinco pasos dado al final de la Sección 8.1.
- Paso 1. El supuesto natural es que el nuevo medicamento no es mejor que el anterior, sino que debe demostrarse que es mejor. Así, si\(\mu\) denota el tiempo promedio hasta que todos los pacientes que reciben el nuevo medicamento experimenten alivio del dolor, la prueba de hipótesis es\[H_0: \mu =3.5\\ \text{vs}\\ H_a:\mu <3.5\; @\; \alpha =0.05\]
- Paso 2. La muestra es grande, pero se desconoce la desviación estándar poblacional (los\(2.1\) minutos corresponden al medicamento antiguo, no al nuevo). Así, el estadístico de prueba es\[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\] y tiene la distribución normal estándar.
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da\[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{3.1-3.5}{1.5/\sqrt{50}}=-1.886\]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(<\)” esta es una prueba de cola izquierda, por lo que hay un solo valor crítico,\(-z_\alpha =-z_{0.005}\), que a partir de la última línea de la Figura 7.1.6 leemos como\(-1.645\). La región de rechazo es\((-\infty ,-1.645]\).
- Paso 5. Como se muestra en\(\PageIndex{2}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que el tiempo promedio hasta que los pacientes experimentan un alivio perceptible del dolor usando el nuevo analgésico es menor que el tiempo promedio para el analgésico estándar.
.png)
Ejemplo\(\PageIndex{2}\)
Una compañía de cosméticos llena sus frascos de\(8\) onzas de crema facial más vendidos mediante una máquina dispensadora automática. La máquina está preparada para dispensar una media de\(8.1\) onzas por frasco. Los factores incontrolables en el proceso pueden alejar la media\(8.1\) y causar un llenado insuficiente o un sobrellenado, ambos de los cuales son indeseables. En tal caso la máquina dispensadora es detenida y recalibrada. Independientemente de la cantidad media dispensada, la desviación estándar de la cantidad dispensada siempre tiene valor\(0.22\) onza. Un ingeniero de control de calidad selecciona rutinariamente\(30\) frascos de la línea de ensamblaje para verificar las cantidades llenadas. En una ocasión, la media de la muestra es\(\bar{x}=8.2\) onzas y la desviación estándar de la muestra es\(s=0.25\) onza. Determinar si hay evidencia suficiente en la muestra para indicar, a\(1\%\) nivel de significancia, que la máquina debe ser recalibrada.
Solución:
- Paso 1. La suposición natural es que la máquina está funcionando correctamente. Así, si\(\mu\) denota la cantidad media de crema facial que se dispensa, la prueba de hipótesis es\[H_0: \mu =8.1\\ \text{vs}\\ H_a:\mu \neq 8.1\; @\; \alpha =0.01\]
- Paso 2. La muestra es grande y se conoce la desviación estándar poblacional. Así, el estadístico de prueba es\[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}\] y tiene la distribución normal estándar.
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da\[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}=\frac{8.2-8.1}{0.22/\sqrt{30}}=2.490\]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(\neq\)” esta es una prueba de dos colas, por lo que hay dos valores críticos\(\pm z_{\alpha /2}=\pm z_{0.005}\), que a partir de la última línea en la Figura 7.1.6 “Valores críticos de" leemos como\(\pm 2.576\). La región de rechazo es\((-\infty ,-2.576]\cup [2.576,\infty )\).
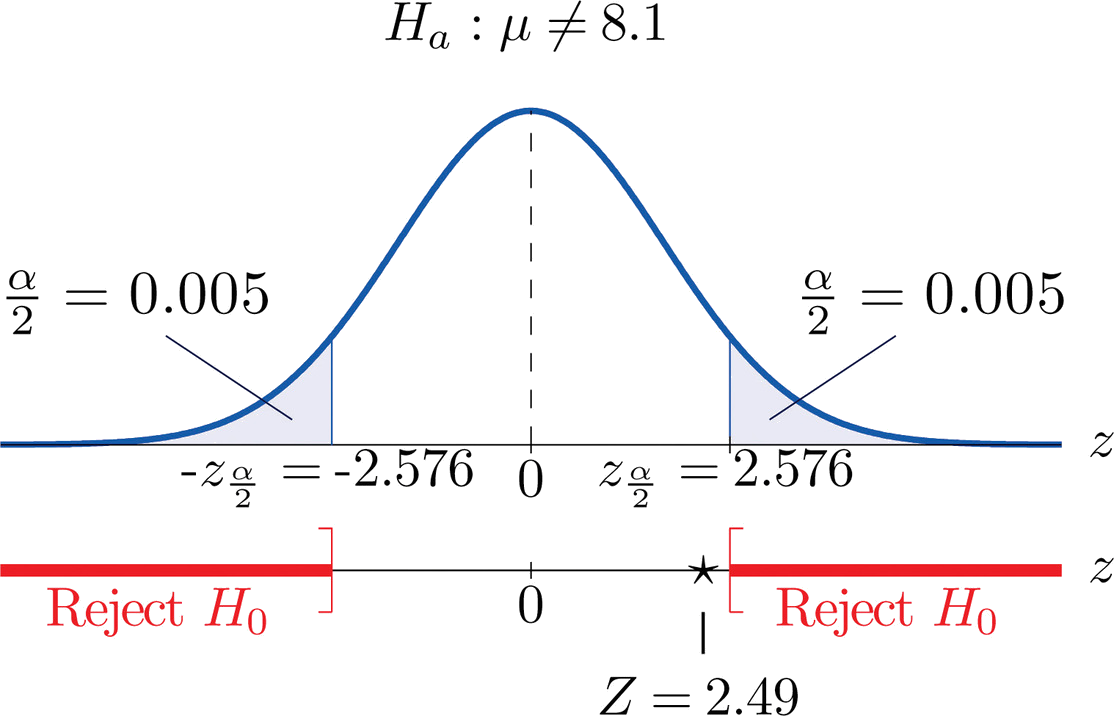
- Paso 5. Como se muestra en\(\PageIndex{3}\) la Figura el estadístico de prueba no cae en la región de rechazo. La decisión es no rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos no proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que la cantidad promedio de producto dispensado es diferente de la\(8.1\) onza. Concluimos que la máquina no necesita ser recalibrada.
Llave para llevar
- Existen dos fórmulas para el estadístico de prueba en las hipótesis de prueba sobre una media poblacional con muestras grandes. Ambas estadísticas de prueba siguen la distribución normal estándar.
- Se utiliza la desviación estándar poblacional si se conoce, de lo contrario se utiliza la desviación estándar de la muestra.
- El mismo procedimiento de cinco pasos se utiliza con cualquiera de los dos estadísticos de prueba.

