3.1: Grados, horas y kilómetros- datos de medición

Es extremadamente importante que la temperatura y la distancia cambien de manera suave y continua. Esto quiere decir, que si tenemos dos medidas diferentes de la temperatura, siempre podemos imaginar un valor intermedio. Dos mediciones de temperatura o distancia forman un intervalo que incluye una cantidad infinita de otros valores posibles. Así, nuestro primer tipo de datos se llama medición, o intervalo. Los datos de medición son similares a la regla sin fin ideal donde cada marca corresponde a un número real.

Sin embargo, los datos de medición no siempre cambian suavemente y continuamente de infinito negativo a infinito positivo. Por ejemplo, la temperatura corresponde a un rayo y no a una línea ya que está limitada con un cero absoluto (\(0^\circ\)K), y el acuerdo es que por debajo de él no es posible la temperatura. Pero el resto de los puntos de temperatura a lo largo de su rango siguen siendo comparables con los números reales.

Es aún más interesante medir ángulos. Los ángulos cambian continuamente, ¡pero después de 359\(^\circ\) va 0\(^\circ\)! En lugar de una línea, hay un segmento con sólo valores positivos. Es por ello que existe una estadística circular especial que trata de ángulos.

A veces, la recopilación de datos de medición requiere equipos costosos o raros y protocolos complejos. Por ejemplo, para estimar los colores de las flores como una variable continua, tendrías (como mínimo) que usar un espectrofotómetro para medir la longitud de onda de la luz reflejada (una representación numérica del color visible).

Ahora consideremos otro ejemplo. Digamos, estamos contando a los clientes en una tienda. Si en un día había 947 personas, y 832 en otro, fácilmente podemos imaginar valores intermedios. También es evidente que el primer día hubo más clientes. No obstante, la analogía se rompe cuando consideramos dos números consecutivos (como 832 y 831) porque, como las personas no se cuentan en fracciones, no hay intermedio. Por lo tanto, estos datos corresponden mejor a números naturales que reales. Estos números están ordenados, pero no siempre permiten intermedios y siempre son no negativos. Pertenecen a un tipo diferente de datos de medición, no continuos, sino discretos\(^{[1]}\).

Relacionada con la definición de datos de medición está la idea de parametricidad. Con ese enfoque, los métodos estadísticos inferenciales se dividen en paramétricos y no paramétricos. Los métodos paramétricos están funcionando bien si:

1. El tipo de datos es la medición continua.
2. El tamaño de la muestra es lo suficientemente grande (generalmente no menos de 30 observaciones individuales).
3. La distribución de datos es normal o cercana a ella. Estos datos suelen llamarse “normales”, y esta característica— “normalidad”.

En caso de que al menos uno de los supuestos anteriores sea violado, los datos suelen requerir métodos no paramétricos. Una ventaja importante de las pruebas no paramétricas es su capacidad para tratar datos sin suposiciones previas sobre la distribución. Por otro lado, los métodos paramétricos son más potentes: la probabilidad de encontrar un patrón existente es mayor porque los algoritmos no paramétricos tienden a “enmascarar” las diferencias combinando observaciones individuales en grupos. Además, los métodos no paramétricos para dos y más muestras a menudo sufren de sensibilidad a la desigualdad de las distribuciones de las muestras.

Creemos artificialmente datos normales y no normales:

Código\(\PageIndex{1}\) (R):

rnorm(10)
runif(10)

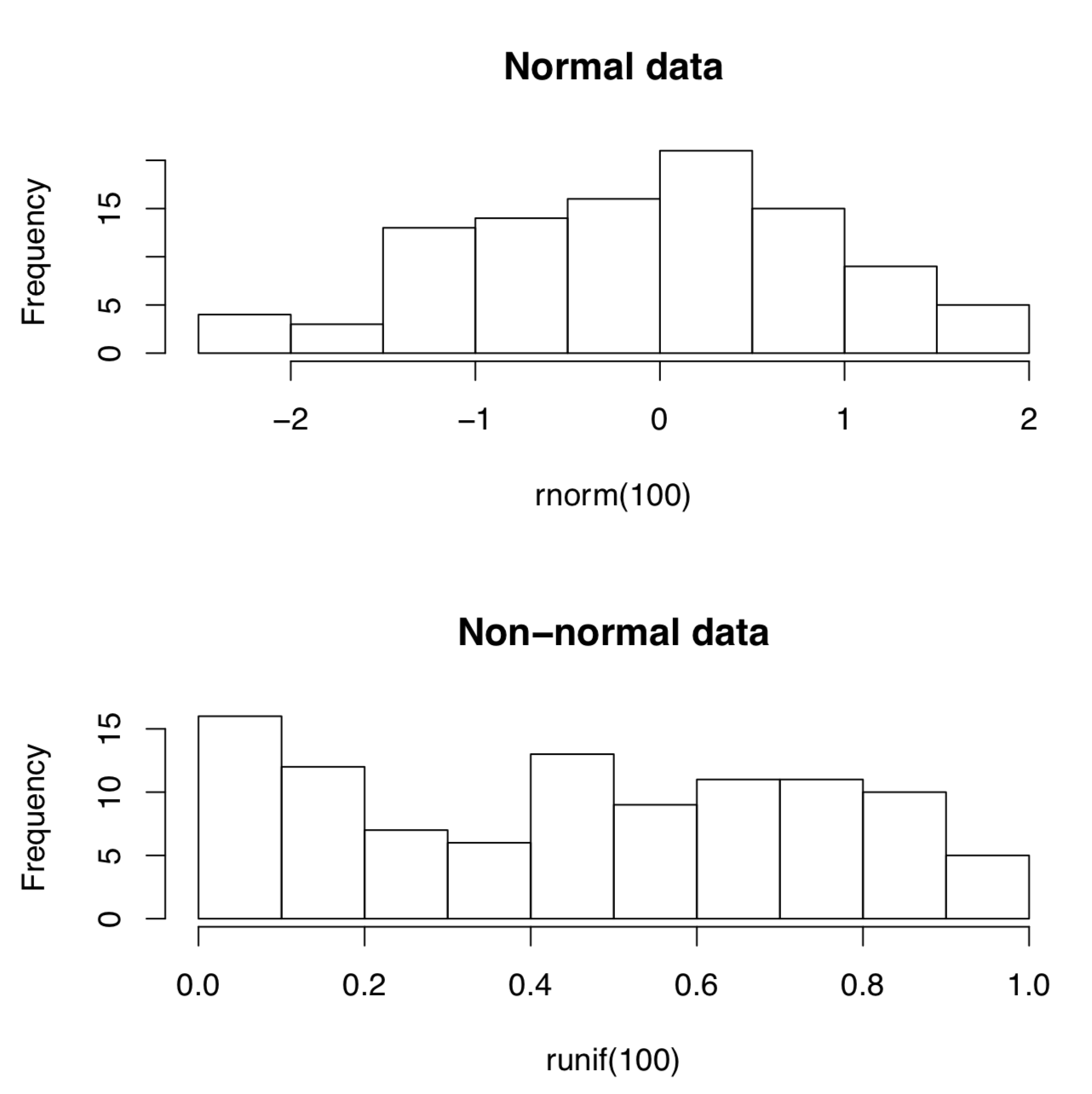
(El primer comando crea 10 números aleatorios que provienen de la distribución normal. Segundo crea números a partir de una distribución uniforme\(^{[2]}\) Mientras que el primer conjunto de números se concentra alrededor de cero, como en el juego de dardos, el segundo conjunto está más o menos igualmente espaciado).

Pero, ¿cómo distinguir lo normal de lo no normal? Lo más sencillo es la forma visual, con parcelas adecuadas (Figura\(\PageIndex{1}\)):

Código\(\PageIndex{2}\) (R):

old.par <- par(mfrow=c(2, 1))
hist(rnorm(100), main="Normal data")
hist(runif(100), main="Non-normal data")
par(old.par)

(¿Ves la diferencia? Los histogramas son buenos para verificar la normalidad, pero hay mejores gráficas; consulte el siguiente capítulo para obtener métodos más avanzados).

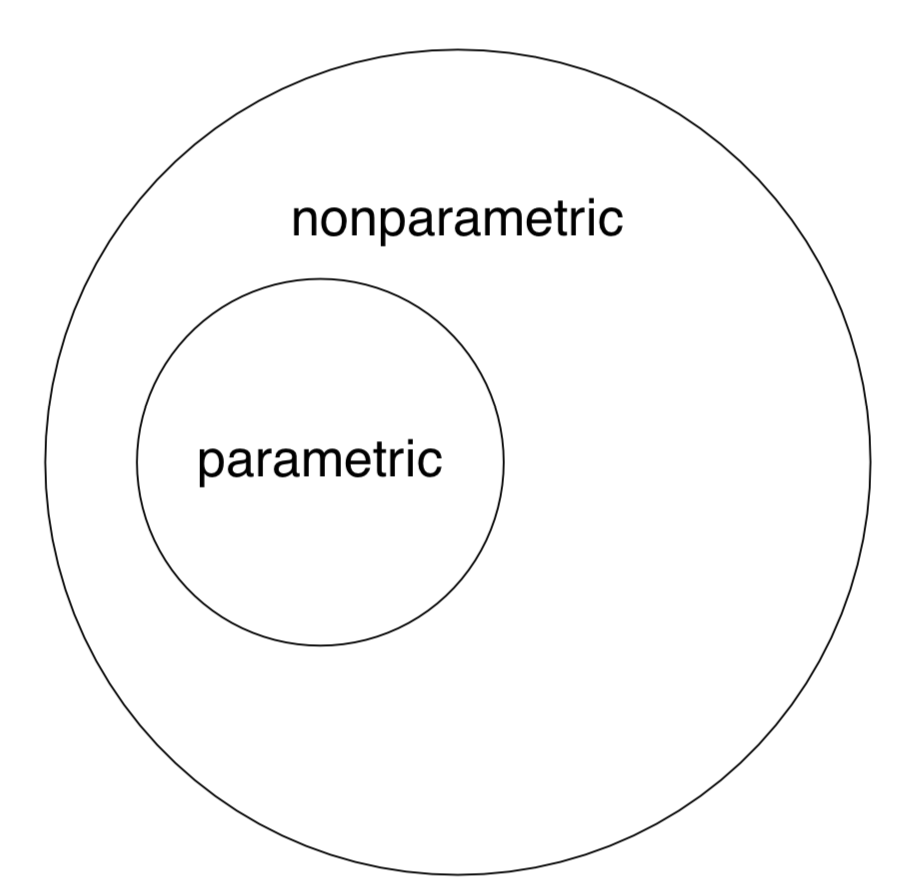
Obsérvese nuevamente que los métodos no paramétricos son aplicables tanto a datos “no paramétricos” como a datos “paramétricos” mientras que lo contrario no es cierto (Figura\(\PageIndex{2}\)).

Por cierto, esta última figura (diagrama de Euler) se creó con R escribiendo los siguientes comandos:

Código\(\PageIndex{3}\) (R):

library(plotrix)
plot(c(-1, 1), c(-1, 1), type="n", xlab="", ylab="", axes=FALSE)
draw.circle(-.2, 0, .4)
draw.circle(.1, 0, .9)
text(-.2, 0, "parametric", cex=1.5)
text(.1, 0.6, "nonparametric", cex=1.5)

(Utilizamos el paquete plotrix que tiene definido el comando draw.circle (). Como ves, uno puede usar R incluso para estos fines exóticos. Sin embargo, los diagramas son mejores para dibujar en aplicaciones especializadas como Inkscape.)

Los datos de medición generalmente se presentan en R como vectores numéricos. A menudo, un vector corresponde con una muestra. Imagínese que tenemos datos sobre alturas (en cm) de los siete empleados de una empresa pequeña. Así es como creamos un vector simple:

Figura\(\PageIndex{1}\) Histogramas de datos normales y no normales.

Código\(\PageIndex{3}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)

Como aprendiste del capítulo anterior, x es el nombre del objeto R, <- es un operador de asignación y c () es una función para crear vector. Cada objeto R tiene una estructura:

Código\(\PageIndex{4}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)
str(x)

La función str () muestra que x es un num, vector numérico. Aquí está la manera de verificar si un objeto es un vector:

Código\(\PageIndex{5}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)
is.vector(x)

Hay muchas funciones similares a is.something () en R, por ejemplo:

Código\(\PageIndex{6}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)
is.numeric(x)

También hay múltiples funciones de conversión como.something ().

Figura\(\PageIndex{2}\) Aplicabilidad de métodos paramétricos y no paramétricos: el diagrama de Euler.

Para ordenar alturas de menor a mayor, utilice:

Código\(\PageIndex{7}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)
sort(x)

Para revertir los resultados, use:

Código\(\PageIndex{8}\) (R):

x <- c(174, 162, 188, 192, 165, 168, 172.5)
rev(sort(x))

Los datos de medición son de alguna manera similares a la regla común, y el paquete R vegan tiene una gráfica linestack () similar a una regla útil para trazar vectores lineales:

Una de las gráficas simples pero útiles es la trama de línea de tiempo linestack () del paquete vegano (Figura\(\PageIndex{3}\)):

Código\(\PageIndex{1}\) (R):

library(vegan)
phanerozoic <- read.table("data/phanerozoic.txt")
with(phanerozoic, linestack(541-V2, labels=paste(V1, V2), cex=1))

Figura\(\PageIndex{3}\) Cronología (Mya) de periodos geológicos fanerozoicos.

En el repositorio abierto, el archivo compositae.txt contiene resultados de mediciones de cabezas de floración para muchas especies de la familia aster (Compositae). En particular, se midió el diámetro total de las cabezas (variable HEAD.D) y se contó el número de rayos (“pétalos”, RAYOS variables, ver Figura\(\PageIndex{4}\)). Por favor, explore parte de estos datos gráficamente, con diagrama (s) de dispersión y descubra si tres especies (manzanilla amarilla, Anthemis tinctoria; cosmos de jardín, Cosmos bipinnatus; y falsa manzanilla, Tripleurospermum inodorum) son diferentes por combinación de diámetro de cabezas y número de rayos.

Figura\(\PageIndex{4}\) Chamomille, Tripleurospermum.: hojas y cabeza (diámetro mostrado) con 15 rayos.

Referencias

1. De hecho, los datos de medición discretos son más útiles para las computadoras: como ya sabrás, los procesadores se basan en la lógica 0/1 y no entienden fácilmente los números flotantes no integrales.

2. Para palabras desconocidas, por favor refiérase al glosario al final del libro.