4.1: Definiciones para Probabilidad

Espacios de muestreo, operaciones de conjunto y modelos de probabilidad

Vayamos directo a las definiciones.

DEFINICIÓN 4.1.1. Supongamos que tenemos un experimento repetible que queremos investigar probabilísticamente. Las cosas que suceden cuando hacemos el experimento, los resultados de ejecutarlo, se llaman los resultados [experimentales]. El conjunto de todos los resultados se llama el espacio muestral del experimento. Casi siempre usamos el símbolo\(S\) para este espacio muestral.

EJEMPLO 4.1.2. Supongamos que el experimento que estamos haciendo es “voltear una moneda”. Entonces el espacio muestral sería\(S=\{H, T\}\).

EJEMPLO 4.1.3. Para el experimento “rodar una matriz [normal, de seis lados]”, el espacio de muestra sería\(S=\{1, 2, 3, 4, 5, 6\}\).

EJEMPLO 4.1.4. Para el experimento “tirar dos dados”, el espacio muestral sería\[\begin{aligned} S=\{&11, 12, 13, 14, 15, 16,\\ &21, 22, 23, 24, 25, 26\\ &31, 23, 33, 34, 35, 36\\ &41, 42, 43, 44, 45, 46\\ &51, 52, 53, 54, 55, 56\\ &61, 62, 63, 64, 65, 66\\\end{aligned}\] donde la notación “\(nm\)” significa “\(1^{st}\)rollo resultó en un\(n\),\(2^{nd}\) en un”\(m\).

EJEMPLO 4.1.5. Considera el experimento “voltear una moneda tantas veces como sea necesario para ver la primera Cabeza”. Esto tendría el espacio muestral infinito\[S=\{H, TH, TTH, TTTH, TTTTH, \dots \} \quad .\]

EJEMPLO 4.1.6. Por último, supongamos que el experimento es “apuntar un contador Geiger a un terrón de material radiactivo y ver cuánto tiempo hay que esperar hasta el siguiente clic”. Entonces el espacio muestral\(S\) es el conjunto de todos los números reales positivos, porque potencialmente el tiempo de espera podría ser cualquier cantidad de tiempo positiva.

Como se mencionó en la introducción del capítulo, estamos más interesados en

DEFINICIÓN 4.1.7. Dado un experimento repetible con espacio de muestra\(S\), un evento es cualquier colección de [algunos, todos o ninguno de los] resultados en\(S\); es decir, un evento es cualquier subconjunto\(E\) de \(S\), escrito\(E\subset S\).

Hay un conjunto especial que es un subconjunto de cualquier otro conjunto, y por lo tanto es un evento en cualquier espacio de muestra.

DEFINICIÓN 4.1.8. El conjunto\(\{\}\) sin elementos se llama el conjunto vacío, para lo cual usamos la notación\(\emptyset\).

EJEMPLO 4.1.9. Al observar el espacio de muestra\(S=\{H, T\}\) en el Ejemplo 4.1.2, está bastante claro que los siguientes son todos los subconjuntos de\(S\):\[\begin{aligned} &\emptyset\\ &\{H\}\\ &\{T\}\\ &S\ [=\{H, T\}]\end{aligned}\]

Dos partes de ese ejemplo son siempre verdaderas:\(\emptyset\) y siempre\(S\) son subconjuntos de cualquier conjunto\(S\).

Como vamos a estar trabajando mucho con eventos, que son subconjuntos de un conjunto más grande, el espacio de muestra, es bueno tener algunos términos básicos de la teoría de conjuntos:

DEFINICIÓN 4.1.10. Dado un subconjunto E S de un conjunto mayor S, el complemento de E, es el conjunto E ^c = {todos los elementos de S que no están en E}.

Si describimos un evento\(E\) en palabras como todos los resultados satisfacen alguna propiedad\(X\), el evento complementario, que consiste en todos los resultados no en\(E\), puede describirse como todos los resultados que no satisfacen \(X\). En otras palabras, a menudo describimos el evento\(E^c\) como el evento “no”\(E\).

DEFINICIÓN 4.1.11. Dado dos sets\(A\) y\(B\), su unión es el conjunto\[A\cup B = \{\text{all elements which are in A or B [or both]}\}\ .\]

Ahora bien, si el evento\(A\) es que esos resultados tienen propiedad\(X\) y\(B\) son aquellos con propiedad\(Y\), el evento\(A\cup B\), con todos los resultados\(A\) junto con todos los resultados en\(B\) lata ser descrito como todos los resultados satisfactorios\(X\) o\(Y\), así a veces pronunciamos el evento “\(A\cup B\)” como “\(A\)o”\(B\).

DEFINICIÓN 4.1.12. Dados dos conjuntos\(A\) y\(B\), su intersección es el conjunto\[A\cap B = \{\text{all elements which are in both A and B}\}\ .\]

Si, como antes, el evento\(A\) consiste en aquellos resultados que tienen propiedad\(X\) y\(B\) son aquellos con propiedad\(Y\), el evento\(A\cap B\) consistirá en aquellos resultados que satisfagan tanto\(X\) y \(Y\). En otras palabras, “\(A\cap B\)” puede describirse como “\(A\)y”\(B\).

Armando la idea de intersección con la idea de ese subconjunto especial\(\emptyset\) de cualquier conjunto, obtenemos el

DEFINICIÓN 4.1.13. Dos conjuntos\(A\) y\(B\) se llaman disjoint if\(A\cap B=\emptyset\). En otras palabras, los conjuntos son disjuntos si no tienen nada en común.

Un sinónimo exacto de disjoint que algunos autores prefieren es mutuamente excluyente. Utilizaremos ambos términos indistintamente en este libro.

Ahora estamos listos para la estructura básica de la probabilidad.

DEFINICIÓN 4.1.14. Dado un espacio de muestra\(S\), un modelo de probabilidad encendido\(S\) es la elección de un número real\(P(E)\) para cada evento\(E\subset S\) que satisfaga

1. Para todos los eventos\(E\),\(0\le P(E)\le 1\).
2. \(P(\emptyset)=1\)y\(P(S)=1\).
3. Para todos los eventos\(E\),\(P(E^c)=1-P(E)\).
4. Si\(A\) y\(B\) son cualesquiera dos eventos disjuntos, entonces\(P(A\cup B)=P(A)+P(B)\). [Esto se llama la regla de adición para eventos disjuntos.]

Diagramas de Venn

Los diagramas de Venn son una forma sencilla de mostrar subconjuntos de un conjunto fijo y mostrar las relaciones entre estos subconjuntos e incluso los resultados de varias operaciones de conjunto (como complemento, unión e intersección) en ellos. El uso principal que haremos de los diagramas de Venn es para eventos en un cierto espacio de muestra, por lo que usaremos esa terminología [aunque la técnica tenga una aplicación mucho más amplia].

Para hacer un Diagrama de Venn, siempre empieza haciendo un rectángulo para representar todo el espacio muestral:

Dentro de ese rectángulo, hacemos círculos, óvalos, o simplemente blobs, para indicar esa porción del espacio de muestra que es algún evento\(E\):

En ocasiones, si los resultados en el espacio muestral\(S\) y en el evento\(A\) podrían indicarse en las diferentes partes del diagrama de Venn. Entonces, si\(S=\{a, b, c, d\}\) y\(A=\{a, b\}\subset S\), podríamos dibujar esto como

El complemento\(E^c\) de un evento\(E\) es fácil de mostrar en un diagrama de Venn, ya que es simplemente todo lo que no está en\(E\):

Esto en realidad puede ser útil para averiguar en qué debe estar\(E^c\). En el ejemplo anterior con\(S=\{a, b, c, d\}\) y\(A=\{a, b\}\subset S\), al mirar lo que hay en la parte exterior sombreada para nuestro cuadro de\(E^c\), podemos ver que para eso\(A\), obtendríamos\(A^c=\{c, d\}\).

Pasando ahora a establecer operaciones que funcionen con dos eventos, supongamos que queremos hacer un diagrama de Venn con eventos\(A\) y\(B\). Si sabemos que estos eventos son disjuntos, entonces haríamos el diagrama de la siguiente manera:

mientras que si se sabe que no son disjuntas, usaríamos en su lugar este diagrama:

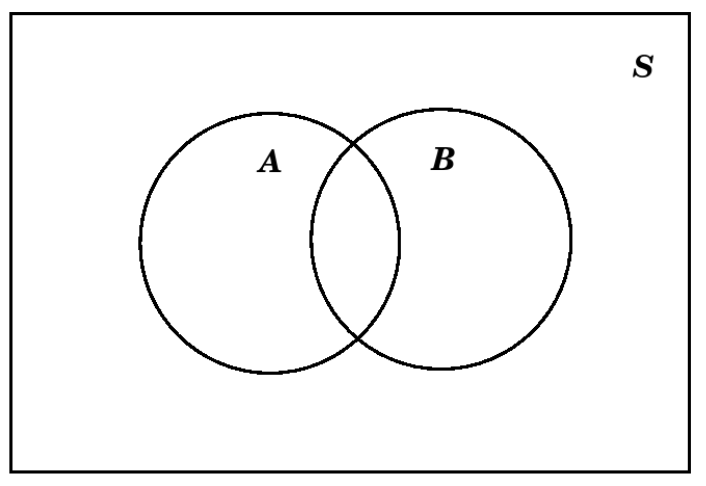
Por ejemplo, eso\(S=\{a, b, c, d\}\)\(A=\{a, b\}\),, y\(B=\{b, c\}\), tendríamos

En caso de duda, probablemente sea mejor usar la versión con solapamiento, que entonces simplemente no podría tener ningún punto en ella (o podría tener probabilidad cero, cuando lleguemos a eso, a continuación).

Los diagramas de Venn son muy buenos para mostrar uniones e intersección:

Otra cosa agradable que hacer con los diagramas de Venn es utilizarlos como ayuda visual para los cálculos de probabilidad. La idea básica es hacer un diagrama que muestre los diversos eventos sentados dentro del rectángulo habitual, que representa el espacio muestral, y poner números en varias partes del diagrama que muestren las probabilidades de esos eventos, o de los resultados de las operaciones (uniones, intersección y complemento) sobre esos eventos .

Por ejemplo, si nos dicen que un evento\(A\) tiene probabilidad\(P(A)=.4\), entonces podemos rellenar inmediatamente\(.4\) lo siguiente:

Pero también podemos poner un número en el exterior de ese círculo que representa\(A\), aprovechando que ese exterior es\(A^c\) y la regla de probabilidades de complementos (punto 3) de la Definición 4.1.14) para concluir que el número apropiado es \(1-.4=.6\):

Recomendamos que, en un diagrama de Venn que muestre valores de probabilidad, siempre ponga un número en la región exterior a todos los eventos [pero dentro del rectángulo que indica el espacio muestral, por supuesto].

Complicando un poco este proceso de poner números de probabilidad en las regiones de un diagrama de Venn es la situación en la que estamos dando tanto para un evento como para un subconjunto subconjunto,\(\subset\) de ese evento. Esto ocurre con mayor frecuencia cuando nos dicen probabilidades tanto de algunos eventos como de su intersección (s). Aquí hay un ejemplo:

EJEMPLO 4.1.15. Supongamos que nos dicen que tenemos dos eventos\(A\) y\(B\) en el espacio muestral\(S\), que satisfacen\(P(A)=.4\),\(P(B)=.5\), y\(P(A\cap B)=.1\). En primer lugar, lo sabemos\(A\) y no\(B\) son disjuntas, ya que si fueran disjuntas, eso significaría (por definición) eso\(A\cap B=\emptyset\), y desde\(P(\emptyset)=0\) pero\(P(A\cap B)\neq 0\), eso no es posible. Así que dibujamos un diagrama de Venn que ya hemos visto antes:

Sin embargo, sería imprudente simplemente escribir esos números dados\(.4\),\(.5\), y\(.1\) en las tres regiones centrales de este diagrama. El motivo es que el número\(.1\) es la probabilidad de\(A\cap B\), que es parte de\(A\) ya, así que si simplemente escribimos\(.4\) en el resto de\(A\), estaríamos contando eso\(.1\) para el \(A\cap B\)dos veces. Por lo tanto, antes de escribir un número en el resto de\(A\), fuera de\(A\cap B\), tenemos que restar el\(.1\) for\(P(A\cap B)\). Eso quiere decir que el número que va en el resto de\(A\) debe ser\(.4-.1=.3\). Un razonamiento similar nos dice que el número en la parte de\(B\) fuera de\(A\cap B\), debería ser\(.5-.1=.4\). Eso significa que el diagrama de Venn con todas las probabilidades escritas sería:

El enfoque en el ejemplo anterior es nuestra segunda recomendación importante sobre a quién poner números en un diagrama de Venn mostrando valores de probabilidad: siempre poner un número en cada región que corresponda a la probabilidad de que esa región conectada más pequeña contenga el número, no cualquier región más grande .

Un último punto debemos hacer, usando el mismo argumento que en el ejemplo anterior. Supongamos que tenemos eventos\(A\) y\(B\) en un espacio muestral\(S\) (de nuevo). Supongamos que no estamos seguros de si\(A\) y\(B\) somos disjuntos, así que no podemos usar la regla de suma para los eventos disjuntos para calcular\(P(A\cup B)\). Pero fíjense que los eventos\(A\) y\(A^c\) son disjuntos, de manera que\(A\cap B\) y también\(A^c\cap B\) son disjuntos y\[A = A\cap S = A\cap\left(B\cup B^c\right) = \left(A\cap B\right)\cup\left(A\cap B^c\right)\] es una descomposición del suceso\(A\) en los dos eventos disjuntos\(A\cap B\) y \(A^c\cap B\). De la regla de adición para eventos disjuntos, esto significa que\[P(A)=P(A\cap B)+P(A\cap B^c)\ .\]

Razonamiento similar nos dice tanto eso\[P(B)=P(A\cap B)+P(A^c\cap B)\] como eso\[A\cup B=\left(A\cap B^c\right)\cup\left(A\cap B\right)\cup\left(A^c\cap B\right)\] es una descomposición de\(A\cup B\) en piezas disjuntas, por lo que\[P(A\cup B)=P(A\cap B^c)+P(A\cap B)+P(A^c\cap B)\ .\] Combinando todas estas ecuaciones, concluimos que\[\begin{aligned} P(A)+P(B)-P(A\cap B) &=P(A\cap B)+P(A\cap B^c)+P(A\cap B)+P(A^c\cap B)-P(A\cap B)\\ &= P(A\cap B^c)+P(A\cap B)+P(A^c\cap B) + P(A\cap B)-P(A\cap B)\\ &= P(A\cap B^c)+P(A\cap B)+P(A^c\cap B)\\ &= P(A\cup B) \ .\end{aligned}\] Esto es lo suficientemente importante como para afirmar como un

HECHO 4.1.16. La regla de adición para eventos generales Si\(A\) y\(B\) son eventos en un espacio de muestra\(S\) entonces tenemos la regla de adición para sus probabilidades\[P(A\cup B) = P(A) + P(B) - P(A\cap B)\ .\] Esta regla es cierta ya sea o no\(A\) y \(B\)son disjuntas.

Modelos de probabilidad finita

Aquí hay una situación agradable en la que podemos calcular fácilmente muchas probabilidades con bastante facilidad: si el espacio muestral\(S\) de algún experimento es finito.

Entonces, supongamos que el espacio muestral consiste solo en los resultados\(S=\{o_1, o_2, \dots, o_n\}\). Para cada uno de los resultados, podemos calcular la probabilidad:\[\begin{aligned} p_1 =& P(\{o_1\})\\ p_2 =& P(\{o_2\})\\ &\vdots\\ p_n =& P(\{o_n\})\\\end{aligned}\] Pensemos en lo que nos dicen las reglas para los modelos de probabilidad sobre estos números\(p_1, p_2, \dots, p_n\). En primer lugar, ya que cada uno es la probabilidad de un evento, vemos que\[\begin{aligned} 0\le &p_1\le 1\\ 0\le &p_2\le 1\\ &\ \vdots\\ 0\le &p_n\le 1\end{aligned}\] Además, ya que\(S=\{o_1, o_2, \dots, o_n\}=\{o_1\}\cup\{o_2\}\cup \dots \cup\{o_n\}\) y todos los eventos\(\{o_1\}, \{o_2\}, \dots, \{o_n\}\) son disjuntos, por la regla de suma para eventos disjuntos tenemos\[\begin{aligned} 1=P(S)&=P(\{o_1, o_2, \dots, o_n\})\\ &=P(\{o_1\}\cup\{o_2\}\cup \dots \cup\{o_n\})\\ &=P(\{o_1\})+P(\{o_2\})+ \dots +P(\{o_n\})\\ &=p_1+p_2+ \dots +p_n\ .\end{aligned}\]

Lo último que hay que notar sobre esta situación de un espacio muestral finito es que si\(E\subset S\) es algún evento, entonces\(E\) será solo una recopilación de algunos de los resultados de\(\{o_1, o_2, \dots, o_n\}\) (tal vez ninguno, tal vez todos, tal vez un número intermedio). Ya que, de nuevo, los eventos como\(\{o_1\}\)\(\{o_2\}\) y así sucesivamente son disjuntos, podemos calcular\[\begin{aligned} P(E) &= P(\{\text{the outcomes $o_j$ which make up $E$}\})\\ &= \sum \{\text{the $p_j$'s for the outcomes in $E$}\}\ .\end{aligned}\]

En otras palabras

HECHO 4.1.17. Un modelo de probabilidad en un espacio muestral\(S\) con un número finito\(n\),, de resultados, no es otra cosa que una elección de números reales\(p_1, p_2, \dots, p_n\), todo en el rango de\(0\) a\(1\) y satisfactorio\(p_1+p_2+ \dots +p_n=1\). Para tal elección de números, podemos calcular la probabilidad de cualquier evento\(E\subset S\) como\[P(E) = \sum \{\text{the p_j's corresponding to the outcomes o_j which make up E}\}\ .\]

EJEMPLO 4.1.18. Para el giro de moneda del Ejemplo 4.1.2, solo están los dos resultados\(H\) y\(T\) para los cuales necesitamos escoger dos probabilidades, llamarlas\(p\) y\(q\). De hecho, ya que el total debe ser\(1\), eso lo sabemos\(p+q=1\) o, en otras palabras,\(q=1-p\). Las probabilidades para todos los eventos (que enumeramos en el Ejemplo 4.1.9) son\[\begin{aligned} P(\emptyset) &= 0\\ P(\{H\}) &= p\\ P(\{T\}) &= q = 1-p\\ P(\{H,T\}) &= p + q = 1\end{aligned}\]

Lo que aquí hemos descrito es, potencialmente, una moneda sesgada, ya que no estamos asumiendo que\(p=q\) — no se supone que las probabilidades de obtener una cabeza y una cola sean las mismas. La alternativa es asumir que tenemos una moneda justa, es decir, eso es\(p=q\). Tenga en cuenta que en tal caso, ya que\(p+q=1\), tenemos\(2p=1\) y así\(p=1/2\). Es decir, la probabilidad de una cabeza (y, de igual manera, la probabilidad de una cola) en un solo lanzamiento de una moneda justa es\(1/2\).

EJEMPLO 4.1.19. Al igual que en el ejemplo anterior, podemos considerar el dado del Ejemplo 4.1.3 a un dado justo, es decir, que las probabilidades individuales de cara son todas iguales. Ya que también deben sumar a\(1\) (como vimos para todos los modelos de probabilidad finita), se deduce que entonces\[p_1 = p_2 = p_3 = p_4 = p_5 = p_6 = 1/6 .\] podemos usar esta información básica y la fórmula (for\(P(E)\)) en Fact 4.1.17 para calcular la probabilidad de cualquier evento de interés, como\[P(\text{``roll was even''}) = P(\{2, 4, 6\}) = \frac16 + \frac16 + \frac16 = \frac36 = \frac12\ .\]

Deberíamos inmortalizar estos dos últimos ejemplos con un

[def:fair] Cuando estamos hablando de dados, monedas, individuos para alguna tarea, u otro experimento pequeño, práctico, finito, usamos el término justo para indicar que las probabilidades de todos los resultados individuales son iguales (y por lo tanto todos iguales al número \(1/n\), donde\(n\) es el número de resultados en el espacio muestral). Un término más técnico para la misma idea es equiprobable, mientras que un término más casual que a menudo se usa para esto en entornos muy informales es “al azar” (como “elige una carta al azar de esta baraja” o “elige un paciente al azar” del grupo de estudio para darle el nuevo tratamiento a...”).

EJEMPLO 4.1.21. Supongamos que miramos el experimento del Ejemplo 4.1.4 y agregamos la información de que los dos dados que estamos rodando son justos. Esto en realidad no es suficiente para averiguar las probabilidades, ya que también tenemos que asegurar que el laminado justo del primer dado no afecta de ninguna manera el laminado del segundo dado. Este es técnicamente el requisito de que los dos rollos sean independientes, pero como no lo investigaremos cuidadosamente hasta §2, abajo, digamos aquí simplemente que suponemos que los dos rollos son justos y de hecho no están influenciados por nada que los rodea en el mundo incluyéndose entre sí.

Lo que esto significa es que, a la larga, esperaríamos que el primer dado mostrara un\(1\) aproximado\({\frac16}^{th}\) del tiempo, y a la larga, el segundo dado mostraría\(1\) aproximadamente\({\frac16}^{th}\) de esos tiempos. Esto significa que el resultado del experimento de “tirar dos dados” debería ser\(11\) con probabilidad\(\frac{1}{36}\), y el mismo razonamiento mostraría que todos los resultados tienen esa probabilidad. En otras palabras, este es un espacio muestral equiprobable con\(36\) resultados cada uno teniendo probabilidad\(\frac{1}{36}\). Lo que a su vez nos permite calcular cualquier probabilidad que nos guste, como\[\begin{aligned} P(\text{``sum of the two rolls is $4$''}) &= P(\{13, 22, 31\})\\ &= \frac{1}{36} + \frac{1}{36} + \frac{1}{36}\\ &= \frac{3}{36}\\ &= \frac{1}{12}\ .\end{aligned}\]