10.3: La Función Cuantil
- Page ID
- 150888
La función de cuantil
La función cuantil para una distribución de probabilidad tiene muchos usos tanto en la teoría como en la aplicación de la probabilidad. Si\(F\) es una función de distribución de probabilidad, la función cuantil puede usarse para “construir” una variable aleatoria que tiene\(F\) como función de distribuciones. Este hecho sirve como base de un método de simulación del “muestreo” a partir de una distribución arbitraria con la ayuda de un generador de números aleatorios. Además, dada cualquier clase finita
\(\{X_i: 1 \le i \le n\}\)de variables aleatorias, se\(\{Y_i: 1 \le i \le n\}\) puede construir una clase independiente,\(Y_i\) teniendo cada una\(X_i\) y asociadas la misma distribución (marginal). Las funciones cuantiles para variables aleatorias simples pueden ser utilizadas para obtener un importante teorema de aproximación de Poisson (que no desarrollamos en este trabajo). La función quantile se utiliza para derivar una serie de formas especiales útiles para la expectativa matemática.
Concepto general: propiedades y ejemplos
Si\(F\) es una función de distribución de probabilidad, la función cuantil asociada\(Q\) es esencialmente una inversa de\(F\). La función cuantil se define en el intervalo unitario (0, 1). Para\(F\) continuo y estrictamente creciente en\(t\), luego\(Q(u) = t\) iff\(F(t) = u\). Así, si\(u\) es un valor de probabilidad,\(t = Q(u)\) es el valor de\(t\) para el cual\(P(X \le t) = u\).
Ejemplo 10.3.28: La distribución de Weibull (3, 2, 0)
\(u = F(t) = 1 - e^{-3t^2}\)\(t \ge 0\)\(\Rightarrow\)\(t = Q(u) = \sqrt{-\text{ln } (1 - u)/3}\)
Ejemplo 10.3.29: La distribución normal
La función m-norminv, basada en la función erfinv de MATLAB (función de error inverso), calcula los valores de\(Q\) para la distribución normal.
La restricción al caso continuo no es esencial. Consideramos una definición general que se aplica a cualquier función de distribución de probabilidad.
Definición: Si\(F\) es una función que tiene las propiedades de una función de distribución de probabilidad, entonces la función quantile for\(F\) viene dada por
\(Q(u) = \text{inf } \{t: F(t) \ge u\}\)\(\forall u \in (0, 1)\)
Tomamos nota
- Si\(F(t^{*}) \ge u^{*}\), entonces\(t^{*} \ge \text{inf } \{t: F(t) \ge u^{*}\} = Q(u^{*})\)
- Si\(F(t^{*}) < u^{*}\), entonces\(t^{*} < \text{inf } \{t: F(t) \ge u^{*}\} = Q(u^{*})\)
De ahí que tengamos la propiedad importante:
(Q1)\(Q(u) \le t\) iff\(u \le F(t)\)\(\forall u \in (0, 1)\)
La propiedad (Q1) implica la siguiente propiedad importante:
(Q2) Si\(U\) ~ uniforme (0, 1), entonces\(X = Q(U)\) tiene función de distribución\(F_X = F\). Para ver esto, tenga en cuenta que\(F_X(t) = P(Q(U) \le t] = P[U \le F(t)] = F(t)\).
Propiedad (Q2) implica que si\(F\) es alguna función de distribución, con función cuantil\(Q\), entonces la variable aleatoria\(X = Q(U)\), con\(U\) uniformemente distribuida on (0, 1), tiene función de distribución\(F\).
Ejemplo 10.3.30: Clases independientes con distribuciones prescritas
Supongamos que\(\{X_i: 1 \le i \le n\}\) es una clase arbitraria de variables aleatorias con funciones de distribución correspondientes\(\{F_i : 1 \le i \le n\}\). \(\{Q_i: 1 \le i \le n\}\)Dejen ser las respectivas funciones cuantiles. Siempre hay un uniforme\(\{U_i: 1 \le i \le n\}\) iid de clase independiente (0, 1) (marginales para la distribución uniforme conjunta en la unidad hipercubo con lados (0, 1)). Entonces las variables aleatorias\(Y_i = Q_i (U_i)\)\(1 \le i \le n\),, forman una clase independiente con los mismos marginales que la\(X_i\).
Se pueden establecer otras propiedades importantes de la función cuantil.
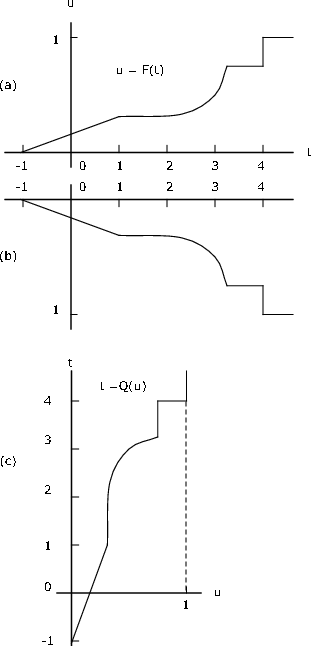
\(Q\)es continuo a la izquierda, mientras que\(F\) es continuo a la derecha.
Si los saltos están representados por segmentos de línea vertical, la construcción de la gráfica de se\(u = Q(t)\) puede obtener mediante el siguiente procedimiento de dos pasos:
- Invertir toda la figura (incluidos los ejes), luego
- Gire la figura resultante 90 grados en sentido antihorario
Esto se ilustra en la Figura 10.3.9. Si los saltos están representados por segmentos de línea verticales, entonces los saltos van a segmentos planos y los segmentos planos van a segmentos verticales.
Si\(X\) es discreto con probabilidad\(p_i\) en\(t_i\)\(1 \le i \le n\), entonces\(F\) tiene saltos en la cantidad\(p_i\) en cada uno\(t_i\) y es constante entre. La función cuantil es una función de paso continuo a la izquierda que tiene valor\(t_i\) en el intervalo\((b_{i - 1}, b_i]\), donde\(b_0 = 0\) y\(b_i = \sum_{j = 1}^{i} p_j\). Esto se puede afirmar
Si\(F(t_i) = b_i\), entonces\(Q(u) = t_i\) para\(F(t_{i - 1}) < u \le F(t_i)\)
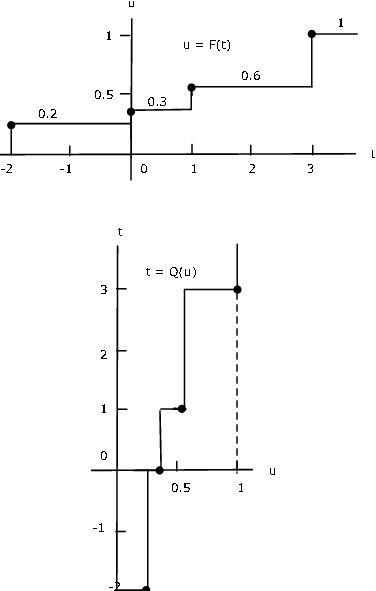
Ejemplo 10.2.31: Función cuantil para una variable aleatoria simple
Supongamos que la variable aleatoria simple\(X\) tiene distribución
\(X =\)[-2 0 1 3]\ (PX = [0.2 0.1 0.3 0.4]
La Figura 1 muestra una gráfica de la función de distribución\(F_X\). Se refleja en el eje horizontal luego se gira en sentido antihorario para dar la gráfica de\(Q(u\) versus\(u\).
Utilizamos la caracterización analítica anterior en el desarrollo de una serie de funciones m y procedimientos m.
m-procedimientos para una variable aleatoria simple
La base para los cálculos de función cuantil para una variable aleatoria simple es la fórmula anterior. Esto se implementa en la función m dquant, que se utiliza como elemento de varios procedimientos de simulación. Para trazar la función quantile, utilizamos dquanplot que emplea la función stairs y plot\(X\) vs la función de distribución\(FX\). El procedimiento dsample emplea dquant para obtener una “muestra” de una población con distribución simple y para calcular frecuencias relativas de los diversos valores.
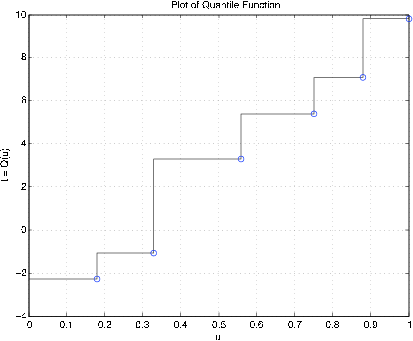
Ejemplo 10.3.32: Variable aleatoria simple
X = [-2.3 -1.1 3.3 5.4 7.1 9.8];
PX = 0.01*[18 15 23 19 13 12];
dquanplot
Enter VALUES for X X
Enter PROBABILITIES for X PX % See Figure 10.3.11 for plot of results
rand('seed',0) % Reset random number generator for reference
dsample
Enter row matrix of values X
Enter row matrix of probabilities PX
Sample size n 10000
Value Prob Rel freq
-2.3000 0.1800 0.1805
-1.1000 0.1500 0.1466
3.3000 0.2300 0.2320
5.4000 0.1900 0.1875
7.1000 0.1300 0.1333
9.8000 0.1200 0.1201
Sample average ex = 3.325
Population mean E[X] = 3.305
Sample variance = 16.32
Population variance Var[X] = 16.33
A veces es deseable saber cuántos ensayos se requieren para alcanzar un cierto valor, o uno de un conjunto de valores. Hay un par de procedimientos m disponibles para la simulación de ese problema. El primero se llama targetset. Se llama a la distribución de la población y luego a la designación de un “conjunto objetivo” de posibles valores. El segundo procedimiento, targetrun, pide el número de repeticiones del experimento, y pide que se alcance el número de miembros del objetivo establecido. Una vez realizadas las corridas, se calculan y muestran diversas estadísticas sobre las corridas.
X = [-1.3 0.2 3.7 5.5 7.3]; % Population values PX = [0.2 0.1 0.3 0.3 0.1]; % Population probabilities E = [-1.3 3.7]; % Set of target states targetset Enter population VALUES X Enter population PROBABILITIES PX The set of population values is -1.3000 0.2000 3.7000 5.5000 7.3000 Enter the set of target values E Call for targetrun
rand('seed',0) % Seed set for possible comparison
targetrun
Enter the number of repetitions 1000
The target set is
-1.3000 3.7000
Enter the number of target values to visit 2
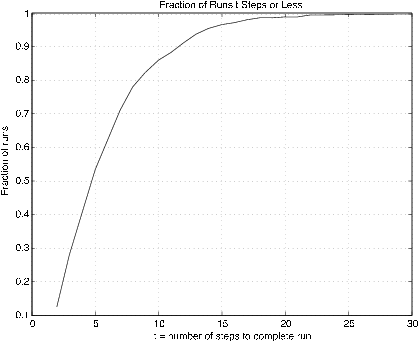
The average completion time is 6.32
The standard deviation is 4.089
The minimum completion time is 2
The maximum completion time is 30
To view a detailed count, call for D.
The first column shows the various completion times;
the second column shows the numbers of trials yielding those times
% Figure 10.6.4 shows the fraction of runs requiring t steps or less
m-procedimientos para funciones de distribución
Un procedimiento dfsetup utiliza la función de distribución para establecer una distribución simple aproximada. El procedimiento m quanplot se utiliza para trazar la función quantile. Este procedimiento es esencialmente el mismo que dquanplot, excepto que se usa la función plot ordinaria en el caso continuo mientras que la función de trazado stairs se usa en el caso discreto. Se utiliza el procedimiento m qsample para obtener una muestra de la población. Dado que hay tantos valores posibles, estos no se muestran como en el caso discreto.
Ejemplo 10.3.34: Función cuantil asociada a una función de distribución
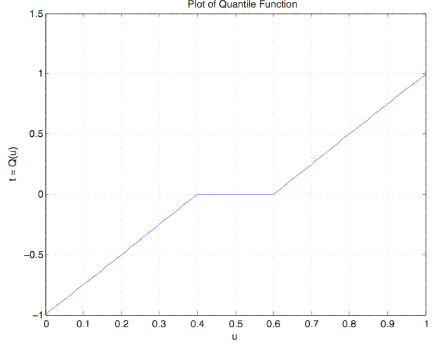
F = '0.4*(t + 1).*(t < 0) + (0.6 + 0.4*t).*(t >= 0)'; % String dfsetup Distribution function F is entered as a string variable, either defined previously or upon call Enter matrix [a b] of X-range endpoints [-1 1] Enter number of X approximation points 1000 Enter distribution function F as function of t F Distribution is in row matrices X and PX quanplot Enter row matrix of values X Enter row matrix of probabilities PX Probability increment h 0.01 % See Figure 10.3.13 for plot qsample Enter row matrix of X values X Enter row matrix of X probabilities PX Sample size n 1000 Sample average ex = -0.004146 Approximate population mean E(X) = -0.0004002 % Theoretical = 0 Sample variance vx = 0.25 Approximate population variance V(X) = 0.2664
m-procedimientos para funciones de densidad
Se utiliza un procedimiento m- acsetup para obtener la distribución aproximada simple. Esto es esencialmente lo mismo que el procedimiento tuappr, excepto que la función de densidad se ingresa como una variable de cadena. Entonces se utilizan los procedimientos quanplot y qsample como en el caso de las funciones de distribución.
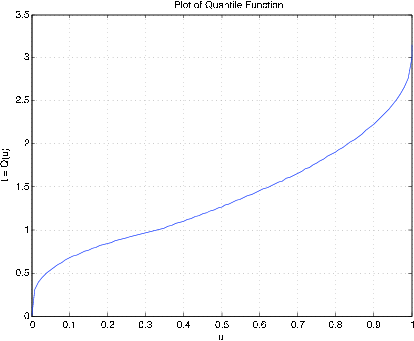
Ejemplo 10.3.35: Función cuantil asociada a una función de densidad
acsetup
Density f is entered as a string variable.
either defined previously or upon call.
Enter matrix [a b] of x-range endpoints [0 3]
Enter number of x approximation points 1000
Enter density as a function of t '(t.^2).*(t<1) + (1- t/3).*(1<=t)'
Distribution is in row matrices X and PX
quanplot
Enter row matrix of values X
Enter row matrix of probabilities PX
Probability increment h 0.01 % See Figure 10.3.14 for plot
rand('seed',0)
qsample
Enter row matrix of values X
Enter row matrix of probabilities PX
Sample size n 1000
Sample average ex = 1.352
Approximate population mean E(X) = 1.361 % Theoretical = 49/36 = 1.3622
Sample variance vx = 0.3242
Approximate population variance V(X) = 0.3474 % Theoretical = 0.3474