10.2: Función de vectores aleatorios
- Page ID
- 150887
Introducción
El enfoque general de mapeo para una sola variable aleatoria y la alternativa discreta se extiende a funciones de más de una variable. Es conveniente considerar el caso de dos variables aleatorias, consideradas conjuntamente. Las extensiones a más de dos variables aleatorias se hacen de manera similar, aunque los detalles son más complicados.
El enfoque general se extendió a un par
Considera un par\(\{X, Y\}\) que tiene distribución conjunta en el plano. El enfoque es análogo al de una sola variable aleatoria con distribución en la línea.
Para encontrar\(P((X, Y) \in Q)\).
- Enfoque de mapeo. Simplemente encuentre la cantidad de masa de probabilidad mapeada en el conjunto\(Q\) en el plano por el vector aleatorio\(W = (X, Y)\).
- En el caso absolutamente continuo, calcule\(\int \int_Q f_{XY}\).
- En el caso discreto, identificar aquellos valores vectoriales\((t_i, u_j)\) de los\((X, Y)\) cuales están en el conjunto\(Q\) y sumar las probabilidades asociadas.
- Alternativa discreta. Considere cada valor vectorial\((t_i, u_j)\) de\((X, Y)\). Seleccione aquellos que cumplan con las condiciones definitorias\(Q\) y agregue las probabilidades asociadas. Este es el enfoque que utilizamos en los cálculos de MATLAB. No requiere que describamos geométricamente la región\(Q\).
Para encontrar\(P(g(X,Y) \in M)\). \(g\)es real valorado y\(M\) es un subconjunto la línea real.
- Enfoque de mapeo. Determine el conjunto\(Q\) de todos aquellos\((t, u)\) que son mapeados\(M\) por la función\(g\). Ahora
\(W(\omega) = (X(\omega), Y(\omega)) \in Q\)iff\(g((X(\omega), Y(\omega)) \in M\) Por lo tanto
\(\{\omega: g(X(\omega), Y(\omega)) \in M\} = \{\omega: (X(\omega), Y(\omega)) \in Q\}\)
Dado que estos son el mismo evento, deben tener la misma probabilidad. Una vez\(Q\) identificado en el plano, determine\(P((X, Y) \in Q)\) de la manera habitual (ver parte a, arriba).
- Alternativa discreta. Para cada posible valor vectorial\((t_i, u_j)\) de\((X, Y)\), determinar si\(g(t_i, u_j)\) cumple con la condición definitoria para\(M\). Seleccione los\((t_i, u_j)\) que sí y agregue las probabilidades asociadas.
Ilustramos el enfoque de mapeo en el caso absolutamente continuo. Un elemento clave en el enfoque es encontrar el conjunto\(Q\) en el plano tal que\(g(X, Y) \in M\) iff\((X, Y) \in Q\). La probabilidad deseada se obtiene integrando\(f_{XY}\) sobre\(Q\).
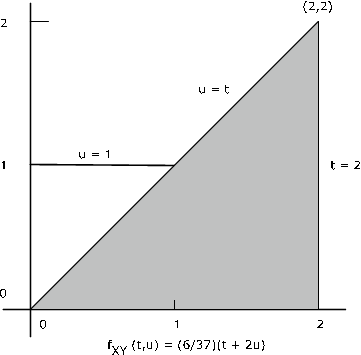
Ejemplo 10.2.15. Un ejemplo numérico
El par\(\{X, Y\}\) tiene densidad de juntas\(f_{XY} (t, u) = \dfrac{6}{37} (t + 2u)\) en la región delimitada por\(t = 0\),\(t = 2\),\(u = 0\),\(u = \text{max} \{1, t\}\) (ver Figura 1). Determinar\(P(Y \le X) = P(X - Y \ge 0)\). Aquí\(g(t, u) = t - u\) y\(M = [0, \infty)\). Ahora\(Q = \{(t, u) : t - u \ge 0\} = \{(t, u) : u \le t \}\) que es la región en el plano sobre o por debajo de la línea\(u = t\). El examen de la figura muestra que para esta región,\(f_{XY}\) es diferente de cero en el triángulo delimitado por\(t = 2\),\(u = 0\), y\(u = t\). La probabilidad deseada es
\(P(Y \le X) = \int_{0}^{2} \int_{0}^{t} \dfrac{6}{37} (t + 2u) du\ dt = 32/37 \approx 0.8649\)
Ejemplo 10.2.16. La densidad para la suma X + Y
Supongamos que el par\(\{X, Y\}\) tiene densidad de articulación\(f_{XY}\). Determine la densidad para
\(Z = X + Y\)
Solución
\(F_Z (v) = P(X + Y \le v) = P((X, Y) \in Q_v)\)donde\(Q_v = \{(t, u) : t + u \le v\} = \{(t, u): u \le v - t\}\)
Para cualquier fijo\(v\), la región\(Q_v\) es la porción del plano en o por debajo de la línea\(u = v - t\) (ver Figura 10.2.2). Así
\(F_Z (v) = \int \int_{Q} f_{XY} = \int_{-\infty}^{\infty} \int_{-\infty}^{v - t} f_{XY} (t, u) du\ dt\)
Diferenciando con la ayuda del teorema fundamental del cálculo, obtenemos
\(f_Z (v) = \int_{\infty}^{\infty} f_{XY} (t, v - t)\ dt\)
Esta expresividad integral se conoce como una integral de convolución.
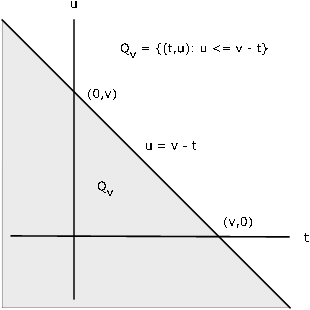
Figura 10.2.2. Región\(Q_v\) para\(X + Y \le v\).
Ejemplo 10.2.17. Suma de variables aleatorias uniformes conjuntas
Supongamos que el par\(\{X, Y\}\) tiene densidad uniforme de junta en el cuadrado de la unidad\(0 \le t \le 1, 0 \le u \le 1\).. Determinar la densidad para\(Z = X + Y\).
Solución
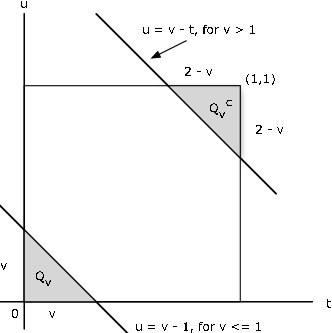
\(F_Z (v)\)es la probabilidad en la región\(Q_v: u \le v - t\). Ahora\(P_{XY} (Q_v) = 1 - P_{XY} (Q_{v}^{c})\), donde el conjunto complementario\(Q_{v}^{c}\) es el conjunto de puntos por encima de la línea. Como muestra la Figura 3, para\(v \le 1\), la parte de la\(Q_v\) cual tiene masa de probabilidad es la región triangular sombreada inferior en la figura, que tiene área (y por lo tanto probabilidad)\(v^2\) /2. Para\(v\) > 1, la región complementaria\(Q_{v}^{c}\) es la región sombreada superior. Tiene área\((2 - v)^2/2\). para que en este caso,\(P_{XY} (Q_v) = 1 - (2 - v)^2/2\). Por lo tanto,
\(F_Z (v) = \dfrac{v^2}{2}\)para\(0 \le v \le 1\) y\(F_Z (v) = 1 - \dfrac{(2 - v)^2}{2}\) para\(1 \le v \le 2\)
La diferenciación muestra que\(Z\) tiene la distribución triangular simétrica en [0, 2], ya que
\(f_Z (v) = v\)para\(0 \le v \le 1\) y\(f_Z(v) = (2 - v)\) para\(1 \le v \le 2\)
Con el uso de funciones indicadoras, éstas pueden combinarse en una sola expresión
\(f_Z (v) = I_{[0, 1]} (v) v + I_{(1, 2]} (2 - v)\)
Solución ALTERNADA
Ya que\(f_{XY} (t, u) = I_{[0, 1]} (t) I_{[0, 1]} (u)\), tenemos\(f_{XY} (t, v - t) = I_{[0, 1]} (t) I_{[0, 1]} (v - t)\). Ahora\(0 \le v - t \le 1\) iff\(v - 1 \le t \le v\), para que
\(f_{XY} (t, v - t) = I_{[0, 1]} (v) I_{[0, v]} (t) + I_{(1, 2]} (v) I_{[v - 1, 1]} (t)\)
Integración con respecto a\(t\) da el resultado anterior.
Independencia de funciones de variables aleatorias independientes
Supongamos que\(\{X, Y\}\) es un par independiente. Vamos\(Z = g(X), W = h(Y)\). Desde
\(Z^{-1} (M) = X^{-1} [g^{-1} (M)]\)y\(W^{-1} (N) = Y^{-1} [h^{-1} (N)]\)
el par\(\{Z^{-1} (M), W^{-1} (N)\}\) es independiente para cada par\(\{M, N\}\). Así, el par\(\{Z, W\}\) es independiente.
Si\(\{X, Y\}\) es un par independiente y\(Z = g(X)\),\(W = g(X)\), entonces el par\(\{Z, W\}\) es independiente. Sin embargo, si\(Z = g(X, Y)\) y\(W = h(X, Y)\), entonces en general no\(\{Z, W\}\) es independiente. Esto se ilustra para variables aleatorias simples con la ayuda del procedimiento m jointzw al final de la siguiente sección.
Ejemplo 10.2.18. Independencia de aproximaciones simples a un par independiente
Supongamos que\(\{X, Y\}\) es un par independiente con aproximaciones simples\(X_s\) y\(Y_s\) como se describe en Aproximaciones de Distribución.
\(X_s = \sum_{i = 1}^{n} t_i I_{E_i} = \sum_{i = 1}^{n} t_i I_{M_i} (X)\)y\(Y_s = \sum_{j = 1}^{m} u_j I_{F_j} = \sum_{j = 1}^{m} u_j I_{N_j} (Y)\)
Como funciones de\(X\) y\(Y\), respectivamente, el par\(\{X_s, Y_s\}\) es independiente. También cada par\(\{I_{M_i}(X), I_{N_j} (Y)\}\) es independiente.
Uso de MATLAB en pares de variables aleatorias simples
En el caso de una sola variable, utilizamos operaciones de matriz sobre los valores de\(X\) para determinar una matriz de valores de\(g(X)\). En el caso de dos variables, debemos usar operaciones de matriz en las matrices de cálculo\(t\) y\(u\) para obtener una matriz\(G\) cuyos elementos son\(g(t_i, u_j)\). Para obtener la distribución para\(Z = g(X, Y)\), podemos usar la función m csort on\(G\) y la matriz de probabilidad conjunta\(P\). Un primer paso, entonces, es el uso de jcalc o icalc para configurar la distribución conjunta y las matrices de cálculo. Esto se ilustra en el siguiente ejemplo.
Ejemplo 10.2.19.
% file jdemo3.m
% data for joint simple distribution
X = [-4 -2 0 1 3];
Y = [0 1 2 4];
P = [0.0132 0.0198 0.0297 0.0209 0.0264;
0.0372 0.0558 0.0837 0.0589 0.0744;
0.0516 0.0774 0.1161 0.0817 0.1032;
0.0180 0.0270 0.0405 0.0285 0.0360];
jdemo3 % Call for data
jcalc % Set up of calculating matrices t, u.
Enter JOINT PROBABILITIES (as on the plane) P
Enter row matrix of VALUES of X X
Enter row matrix of VALUES of Y Y
Use array operations on matrices X, Y, PX, PY, t, u, and P
G = t.^2 -3*u; % Formation of G = [g(ti,uj)]
M = G >= 1; % Calculation using the XY distribution
PM = total(M.*P) % Alternately, use total((G>=1).*P)
PM = 0.4665
[Z,PZ] = csort(G,P);
PM = (Z>=1)*PZ' % Calculation using the Z distribution
PM = 0.4665
disp([Z;PZ]') % Display of the Z distribution
-12.0000 0.0297
-11.0000 0.0209
-8.0000 0.0198
-6.0000 0.0837
-5.0000 0.0589
-3.0000 0.1425
-2.0000 0.1375
0 0.0405
1.0000 0.1059
3.0000 0.0744
4.0000 0.0402
6.0000 0.1032
9.0000 0.0360
10.0000 0.0372
13.0000 0.0516
16.0000 0.0180
Extendemos el ejemplo anterior considerando una función\(W = h(X, Y)\) que tiene una definición compuesta.
Ejemplo 10.2.20. Continuación del ejemplo 10.2.19
Let
\(W = \begin{cases} X & \text{ for } X + Y \ge 1 \\ X^2 + Y^2 & \text{ for } X + Y < 1 \end{cases}\)Determinar la distribución para\(W\)
H = t.*(t+u>=1) + (t.^2 + u.^2).*(t+u<1); % Specification of h(t,u)
[W,PW] = csort(H,P); % Distribution for W = h(X,Y)
disp([W;PW]')
-2.0000 0.0198
0 0.2700
1.0000 0.1900
3.0000 0.2400
4.0000 0.0270
5.0000 0.0774
8.0000 0.0558
16.0000 0.0180
17.0000 0.0516
20.0000 0.0372
32.0000 0.0132
ddbn % Plot of distribution function
Enter row matrix of values W
Enter row matrix of probabilities PW
print % See Figure 10.2.4
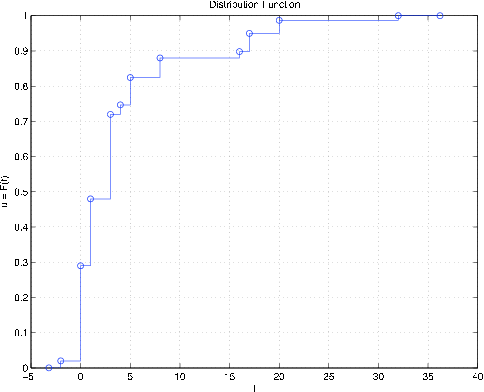
Figura 10.2.4. Distribución para variable aleatoria\(W\) en el Ejemplo 10.2.20.
Distribuciones conjuntas para dos funciones de\((X, Y)\)
En tratamientos previos, utilizamos csort para obtener la distribución marginal para una sola función\(Z = g(X, Y)\). A menudo es deseable tener la distribución conjunta para un par\(Z = g(X, Y)\) y\(W = h(X, Y)\). Como casos especiales, podemos tener\(Z = X\) o\(W = Y\). Supongamos
\(Z\)tiene valores [\(z_1\)\(z_2\)\(\cdot\cdot\cdot\)\(z_c\)] y\(W\) tiene calues [\(w_1\)\(w_2\)\(\cdot\cdot\cdot\)\(w_c\)]
La distribución conjunta requiere la probabilidad de cada par,\(P(W = w_i, Z = z_j)\). Cada par de valores corresponde a un conjunto de pares de\(Y\) valores\(X\) y. Para determinar la matriz de probabilidad conjunta\(PZW\) para\((Z, W)\) arreglado como en el plano, asignamos a cada posición\((i, j)\) la probabilidad\(P(W = w_i, Z=z_j)\), con valores de\(W\) incremento hacia arriba. Cada par de valores (\(W, Z\)) corresponde a uno o más pares de valores (\(Y, X\)). Si seleccionamos y agregamos las probabilidades correspondientes a estos últimos pares, tenemos\(P(W = w_i, Z = z_j)\). Esto se puede lograr de la siguiente manera:
Configurar matrices de cálculo\(t\) y\(u\) como con jcalc.
Utilice la aritmética de matriz para determinar las matrices de valores\(G = [g(t, u)]\) y\(H = [h(t, u)]\).
Utilice csort para determinar las matrices de\(W\) valores\(Z\) y\(PZ\) y las matrices de probabilidad\(PW\) marginal.
Para cada par\((w_i, z_j)\), utilice la función MATLAB find para determinar las posiciones a para las cuales
Asignar a la posición (\(i, j\)) en la matriz de probabilidad conjunta\(PZW\) para (\(Z, W\)) la probabilidad
Primero examinamos los cálculos básicos, que luego se implementan en el procedimiento m jointzw.
Ejemplo 10.2.21. Ilustración de los cálculos básicos de la articulación
% file jdemo7.m
P = [0.061 0.030 0.060 0.027 0.009;
0.015 0.001 0.048 0.058 0.013;
0.040 0.054 0.012 0.004 0.013;
0.032 0.029 0.026 0.023 0.039;
0.058 0.040 0.061 0.053 0.018;
0.050 0.052 0.060 0.001 0.013];
X = -2:2;
Y = -2:3;
jdemo7 % Call for data in jdemo7.m
jcalc % Used to set up calculation matrices t, u
- - - - - - - - - -
H = u.^2 % Matrix of values for W = h(X,Y)
H =
9 9 9 9 9
4 4 4 4 4
1 1 1 1 1
0 0 0 0 0
1 1 1 1 1
4 4 4 4 4
G = abs(t) % Matrix of values for Z = g(X,Y)
G =
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
2 1 0 1 2
[W,PW] = csort(H,P) % Determination of marginal for W
W = 0 1 4 9
PW = 0.1490 0.3530 0.3110 0.1870
[Z,PZ] = csort(G,P) % Determination of marginal for Z
Z = 0 1 2
PZ = 0.2670 0.3720 0.3610
r = W(3) % Third value for W
r = 4
s = Z(2) % Second value for Z
s = 1
Para determinar\(P(W = 4, Z = 1)\), necesitamos determinar las posiciones (\(t, u\)) para las que se toma este par de valores (\(W, Z\)). Por inspección, encontramos que estos son (2,2), (6,2), (2,4) y (6,4). Entonces\(P(W = 4, Z = 1)\) es la probabilidad total en estas posiciones. Esto es 0.001 + 0.052 + 0.058 + 0.001 = 0.112. Ponemos esta probabilidad en la matriz de probabilidad conjunta\(PZW\) en la\(W = 4, Z = 1\) posición. Esto puede ser logrado por MATLAB con las siguientes operaciones.
[i,j] = find((H==W(3))&(G==Z(2))); % Location of (t,u) positions
disp([i j]) % Optional display of positions
2 2
6 2
2 4
6 4
a = find((H==W(3))&(G==Z(2))); % Location in more convenient form
P0 = zeros(size(P)); % Setup of zero matrix
P0(a) = P(a) % Display of designated probabilities in P
P0 =
0 0 0 0 0
0 0.0010 0 0.0580 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0.0520 0 0.0010 0
PZW = zeros(length(W),length(Z)) % Initialization of PZW matrix
PZW(3,2) = total(P(a)) % Assignment to PZW matrix with
PZW = 0 0 0 % W increasing downward
0 0 0
0 0.1120 0
0 0 0
PZW = flipud(PZW) % Assignment with W increasing upward
PZW =
0 0 0
0 0.1120 0
0 0 0
0 0 0
El procedimiento jointzw realiza esta operación para cada par posible de\(W\) y\(Z\) valores (con la operación flipud viniendo solo después de que se hayan realizado todas las asignaciones individuales).
ejemplo 10.2.22. distribución conjunta para z = g (x, y) = ||x| - y| y w = h (x, y) = |xy|
% file jdemo3.m data for joint simple distribution
X = [-4 -2 0 1 3];
Y = [0 1 2 4];
P = [0.0132 0.0198 0.0297 0.0209 0.0264;
0.0372 0.0558 0.0837 0.0589 0.0744;
0.0516 0.0774 0.1161 0.0817 0.1032;
0.0180 0.0270 0.0405 0.0285 0.0360];
jdemo3 % Call for data
jointzw % Call for m-program
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): abs(abs(t)-u)
Enter expression for h(t,u): abs(t.*u)
Use array operations on Z, W, PZ, PW, v, w, PZW
disp(PZW)
0.0132 0 0 0 0
0 0.0264 0 0 0
0 0 0.0570 0 0
0 0.0744 0 0 0
0.0558 0 0 0.0725 0
0 0 0.1032 0 0
0 0.1363 0 0 0
0.0817 0 0 0 0
0.0405 0.1446 0.1107 0.0360 0.0477
EZ = total(v.*PZW)
EZ = 1.4398
ez = Z*PZ' % Alternate, using marginal dbn
ez = 1.4398
EW = total(w.*PZW)
EW = 2.6075
ew = W*PW' % Alternate, using marginal dbn
ew = 2.6075
M = v > w; % P(Z>W)
PM = total(M.*PZW)
PM = 0.3390
Al señalarse en el apartado anterior, si\(\{X, Y\}\) es un par independiente y\(Z = g(X)\),
\(W = h(Y)\), entonces el par {\(Z, W\)} es independiente. Sin embargo, si\(Z = g(X, Y)\) y
\(W = h(X, Y)\), entonces en general el par {\(Z, W\)} no es independiente. Podemos ilustrar esto con la ayuda del procedimiento m jointzw
Ejemplo 10.2.23. Funciones de variables aleatorias independientes
jdemo3
itest
Enter matrix of joint probabilities P
The pair {X,Y} is independent % The pair {X,Y} is independent
jointzw
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): t.^2 - 3*t % Z = g(X)
Enter expression for h(t,u): abs(u) + 3 % W = h(Y)
Use array operations on Z, W, PZ, PW, v, w, PZW
itest
Enter matrix of joint probabilities PZW
The pair {X,Y} is independent % The pair {g(X),h(Y)} is independent
jdemo3 % Refresh data
jointzw
Enter joint prob for (X,Y): P
Enter values for X: X
Enter values for Y: Y
Enter expression for g(t,u): t+u % Z = g(X,Y)
Enter expression for h(t,u): t.*u % W = h(X,Y)
Use array operations on Z, W, PZ, PW, v, w, PZW
itest
Enter matrix of joint probabilities PZW
The pair {X,Y} is NOT independent % The pair {g(X,Y),h(X,Y)} is not indep
To see where the product rule fails, call for D % Fails for all pairs
Caso absolutamente continuo: análisis y aproximación
Al igual que en el análisis Distribuciones Conjuntas, podemos establecer una aproximación simple a la distribución conjunta y proceder como para variables aleatorias simples. En esta sección, resolvemos varios ejemplos analíticamente, luego obtenemos aproximaciones simples.
Ejemplo 10.2.24. Distribución para un producto
Supongamos que el par\(\{X, Y\}\) tiene densidad de articulación\(f_{XY}\). Vamos\(Z = XY\). Determinar\(Q_v\) tal que\(P(Z \le v) = P((X, Y) \in Q_v)\).
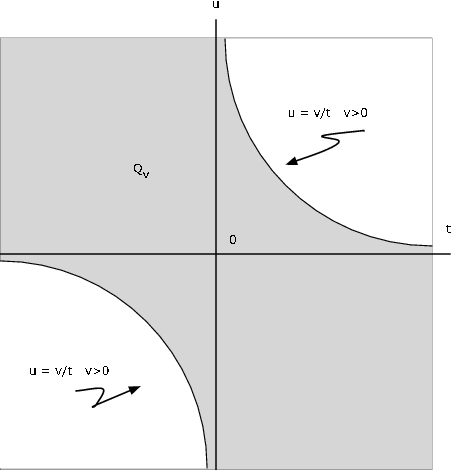
Solución
\(Q_v = \{(t, u) : tu \le v\} = \{(t, u): t > 0, u \le v/t\} \bigvee \{(t, u) : t < 0, u \ge v/t\}\}\)
Ejemplo 10.2.25.
\(\{X, Y\}\)~ uniforme en el cuadrado de la unidad
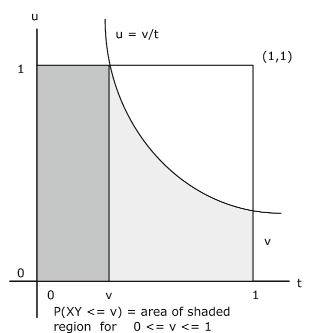
\(f_{XY} (t, u) = 1\). Luego (ver Figura 10.2.6)
\(P(XY \le v) = \int \int_{Q_v} 1 du\ dt\)donde\(Q_v = \{(t, u): 0 \le t \le 1, 0 \le u \le \text{min } \{1, v/t\}\}\)
Espectáculos de integración
\(F_Z (v) = P(XY \le v) = v(1 - \text{ln } (v))\)de manera que\(f_Z (v) = - \text{ln } (v) = \text{ln } (1/v)\),\(0 < v \le 1\)
Para\(v = 0.5\),\(F_Z (0.5) = 0.8466\).
% Note that although f = 1, it must be expressed in terms of t, u. tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (u>=0)&(t>=0) Use array operations on X, Y, PX, PY, t, u, and P G = t.*u;
[Z,PZ] = csort(G,P); p = (Z<=0.5)*PZ' p = 0.8465 % Theoretical value 0.8466, above
Ejemplo 10.2.26. Continuación del ejemplo 5 de “Vectores aleatorios y distribuciones conjuntas”
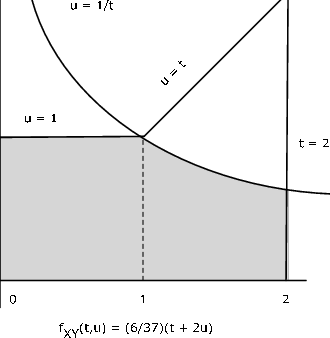
El par\(\{X, Y\}\) tiene densidad de juntas\(f_{XY} (t, u) = \dfrac{6}{37} (t + 2u)\) en la región delimitada por\(t = 0\),\(t = 2\) y\(u = \text{max } \{1, t\}\) (ver Figura 7). Vamos\(Z = XY\). Determinar\(P(Z \le 1)\).
Solución Analítica
La referencia a la Figura 10.2.7 muestra que
\(P((X, Y) \in Q = \dfrac{6}{37} \int_{0}^{1} \int_{0}^{1} (t + 2u) du\ dt + \dfrac{6}{37} \int_{1}^{2} \int_{0}^{1/t} (t + 2u) du\ dt = 9/37 + 9/37 = 18/37 \approx 0.4865\)
Solución Aproximada
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 300 Enter number of Y approximation points 300 Enter expression for joint density (6/37)*(t + 2*u).*(u<=max(t,1)) Use array operations on X, Y, PX, PY, t, u, and P Q = t.*u<=1; PQ = total(Q.*P) PQ = 0.4853 % Theoretical value 0.4865, above G = t.*u; % Alternate, using the distribution for Z [Z,PZ] = csort(G,P); PZ1 = (Z<=1)*PZ' PZ1 = 0.4853
En el siguiente ejemplo, la función\(g\) tiene una definición compuesta. Es decir, tiene una regla diferente para diferentes partes del avión.
Ejemplo 10.2.27. Una función compuesta
El par\(\{X, Y\}\) tiene densidad de juntas\(f_{XY} (t, u) = \dfrac{2}{3} (t + 2u)\) en la unidad cuadrada\(0 \le t \le 1\),\(0 \le u \le 1\).
\(Z = \begin{cases} X & \text{for } X^2 - Y \ge 0 \\ X + Y & \text{for } X^2 - Y < 0 \end{cases} = I_Q (X, Y) Y + I_{Q^c} (X, Y) (X + Y)\)
para\(Q = \{(t, u): u \le t^2\}\). Determinar\(P(Z <= 0.5)\).
Solución Analítica
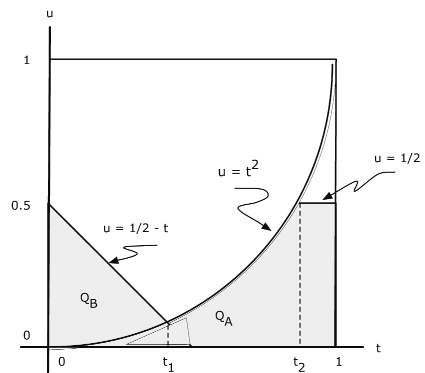
\(P(Z \le 1/2) = P(Y \le 1/2, Y \le X^2) + P(X + Y \le 1/2, Y > X^2) = P((X, Y) \in Q_A \bigvee Q_B)\)
dónde\(Q_A = \{(t, u) : u \le 1/2, u \le t^2\}\) y\(Q_B = \{(t, u): t + u \le 1/2, u > t^2\}\). La referencia a la Figura 10.2.8 muestra que esta es la parte de la unidad cuadrada para la cual\(u \le \text{min } (\text{max } (1/2 - t, t^2), 1/2)\). Podemos romper la integral en tres partes. Dejar\(1/2 - t_1 = t_1^2\) y\(t_2^2 = 1/2\). Entonces
\(P(Z \le 1/2) = \dfrac{2}{3} \int_{0}^{t_1} \int_{0}^{1/2 - t} (t + 2u) du\ dt + \dfrac{2}{3} \int_{t_1}^{t_2} \int_{0}^{t^2} (t + 2u) du\ dt + \dfrac{2}{3} \int_{t_2}^{1} \int_{0}^{1/2} (t + 2u) du \ dt = 0.2322\)
Solución Aproximada
tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (2/3)*(t + 2*u) Use array operations on X, Y, PX, PY, t, u, and P Q = u <= t.^2; G = u.*Q + (t + u).*(1-Q); prob = total((G<=1/2).*P) prob = 0.2328 % Theoretical is 0.2322, above
La configuración de las integrales implica una cuidadosa atención a la geometría del sistema. Una vez establecida, la evaluación es elemental pero tediosa. Por otro lado, la aproximación procede de manera directa a partir de la descripción normal del problema. El resultado numérico se compara bastante estrechamente con el valor teórico y la precisión podría mejorarse tomando más puntos de subdivisión.


