10.1: Problemas de Buffon
- Page ID
- 151964
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los experimentos de Buffon son experimentos aleatorios muy antiguos y famosos, que llevan el nombre del comte de Buffon. Estos experimentos son considerados como uno de los primeros problemas en probabilidad geométrica.
Experimento de monedas de Buffon
El experimento de monedas de Buffon consiste en dejar caer una moneda al azar en un piso cubierto con azulejos de forma idéntica. El evento de interés es que la moneda cruza una grieta entre baldosas. Modelaremos el problema de la moneda de Buffon con fichas cuadradas de longitud lateral 1—suponiendo que la longitud lateral sea 1 equivale a tomar la longitud lateral como unidad de medida.
Supuestos
Primero, definamos matemáticamente el experimento. Como es habitual, idealizaremos los objetos físicos asumiendo que la moneda es un círculo perfecto con radio\(r\) y que las grietas entre las baldosas son segmentos de línea. Una forma natural de describir el resultado del experimento es registrar el centro de la moneda en relación con el centro de la baldosa donde la moneda cae. Más precisamente, construiremos ejes de coordenadas para que la teja donde cae la moneda ocupe el cuadrado\( S = \left[ -\frac{1}{2}, \frac{1}{2} \right]^2 \).
Ahora cuando se arroje la moneda, denotaremos el centro de la moneda por\((X, Y) \in S\) lo que ese\(S\) es nuestro espacio de muestra y\(X\) y\(Y\) son nuestras variables aleatorias básicas. Por último, asumiremos\(r \lt \frac{1}{2}\) eso para que al menos sea posible que la moneda caiga dentro de la plaza sin tocar una grieta.
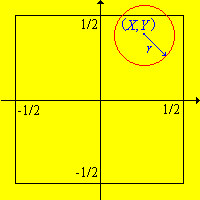
A continuación, necesitamos definir una medida de probabilidad apropiada que describa nuestro vector aleatorio básico\((X, Y)\). Si la moneda cae al azar
en el piso, entonces es natural asumir que\((X, Y)\) se distribuye uniformemente sobre\(S\). Por definición, esto significa que
\[ \P[(X, Y) \in A] = \frac{\area(A)}{\area(S)}, \quad A \subseteq S \]
Ejecuta el experimento de monedas de Buffon con la configuración predeterminada. Observe cómo los puntos parecen llenar el espacio\(S\) muestral de manera uniforme.
La probabilidad de un cruce de grietas
Nuestro interés está en la probabilidad del suceso de\(C\) que la moneda cruce una grieta.
La probabilidad de un cruce de grietas es\(\P(C) - 1 - (1 - 2 r)^2\).
Prueba
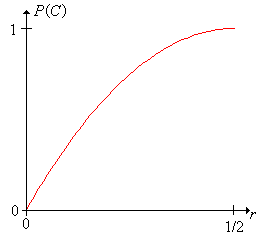
En el experimento de monedas de Buffon, cambia el radio con la barra de desplazamiento y observa cómo cambian los eventos\(C\)\(C^c\) y y. Ejecutar el experimento con diversos valores de\(r\) y comparar el experimento físico con los puntos en la gráfica de dispersión. Comparar la frecuencia relativa de\(C\) a la probabilidad de\(C\).
La convergencia de la frecuencia relativa de un evento (a medida que se repite el experimento) a la probabilidad del evento es un caso especial de la ley de grandes números.
Resuelve el problema de la moneda de Buffon con azulejos rectangulares que tienen altura\(h\) y ancho\(w\).
Contestar
\[1 - \frac{(h - 2 \, r)(w - 2 \, r)}{h \, w}, \quad r \lt \min \left\{ \frac{h}{2}, \frac{w}{2} \right\}\]
Resuelve el problema de la moneda de Buffon con azulejos triangulares equiláteros que tienen una longitud lateral 1.
Recordemos que los números aleatorios son simulación de variables aleatorias independientes, cada una con la distribución uniforme estándar, es decir, la distribución uniforme continua en el intervalo\( (0, 1) \).
Muestra cómo simular el centro de la moneda\((X, Y)\) en el experimento de monedas de Buffon usando números aleatorios.
Contestar
\(X = U - \frac{1}{2}\),\(Y = V - \frac{1}{2}\), donde\(U\) y\(V\) son números aleatorios.
Problema con la aguja de Buffon
El experimento de la aguja de Buffon consiste en dejar caer una aguja sobre un piso de madera dura. El principal evento de interés es que la aguja cruza una grieta entre tablas de entarimado. Por extraño que parezca, ¡la probabilidad de este evento lleva a una estimación estadística del número\(\pi\)!
Supuestos
Nuestro primer paso es definir matemáticamente el experimento. Nuevamente idealizamos los objetos físicos asumiendo que los entarimados son uniformes y que cada uno tiene ancho 1. También asumiremos que la aguja tiene longitud\(L \lt 1\) para que la aguja no pueda cruzar más de una grieta. Finalmente, asumimos que las grietas entre las tablas del entarimado y la aguja son segmentos de línea.
Cuando se deja caer la aguja, queremos registrar su orientación relativa a las grietas del entarimado. Una forma de hacerlo es registrar el ángulo\(X\) que hace la mitad superior de la aguja con la línea a través del centro de la aguja, paralela a las tablas del piso, y la distancia\(Y\) desde el centro de la aguja hasta la grieta inferior. Estas serán las variables aleatorias básicas de nuestro experimento, y así el espacio muestral del experimento es\[ S = [0, \pi) \times [0, 1) = \{(x, y): 0 \le x \lt \pi, \; 0 \le y \lt 1\} \]
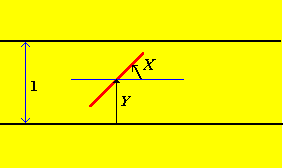
Nuevamente, nuestra principal suposición de modelado es que la aguja es arrojada aleatoriamente
en el piso. Por lo tanto, una suposición matemática razonable podría ser que el vector aleatorio básico\((X, Y)\) se distribuye uniformemente sobre el espacio muestral. Por definición, esto significa que\[ \P[(X, Y) \in A] = \frac{\area(A)}{\area(S)}, \quad A \subseteq S \]
Ejecuta el experimento de aguja de Buffon con la configuración predeterminada y observa los resultados trazados en el espacio de muestra. Observe cómo los puntos en la gráfica de dispersión parecen llenar el espacio\(S\) muestral de manera uniforme.
La probabilidad de un cruce de grietas
Nuestro principal interés está en el caso de\(C\) que la aguja cruce una grieta entre las tablas del piso.
El evento se\(C\) puede escribir en términos de las variables básicas de ángulo y distancia de la siguiente manera:\[ C = \left\{ Y \lt \frac{L}{2} \, \sin(X) \right\} \cup \left\{ Y \gt 1 - \frac{L}{2} \, \sin(X) \right\} \]
Las curvas\(y = \frac{L}{2} \, \sin(x)\) y\(y = 1 - \frac{L}{2} \, \sin(x)\) en el intervalo se\(0 \le x \lt \pi\) muestran en azul en la gráfica de dispersión del experimento de aguja de Buffon, y por lo tanto el evento\(C\) es la unión de las regiones por debajo de la curva inferior y por encima de la curva superior. Así, la aguja cruza una grieta precisamente cuando un punto cae en esta región.
La probabilidad de un cruce de grietas es\(\P(C) = 2 L / \pi\).
Prueba
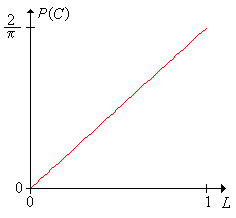
En el experimento de la aguja de Buffon, varíe la longitud de la aguja\(L\) con la barra de desplazamiento y observe cómo\(C\) cambia el evento. Ejecutar el experimento con diversos valores de\(L\) y comparar el experimento físico con los puntos en la gráfica de dispersión. Comparar la frecuencia relativa de\(C\) a la probabilidad de\(C\).
La convergencia de la frecuencia relativa de un evento (a medida que se repite el experimento) a la probabilidad del evento es un caso especial de la ley de grandes números.
Encuentra las probabilidades de los siguientes eventos en el experimento de aguja de Buffon. En cada caso, esboce el evento como un subconjunto del espacio muestral.
- \(\{0 \lt X \lt \pi / 2, \; 0 \lt Y \lt 1 / 3\}\)
- \(\{1 / 4 \lt Y \lt 2 / 3\}\)
- \(\{X \lt Y\}\)
- \(\{X + Y \lt 2\}\)
Contestar
- \(\frac{1}{6}\)
- \(\frac{5}{12}\)
- \(\frac{1}{2 \pi}\)
- \(\frac{3}{2 \pi}\)
La estimación de\( \pi \)
Supongamos que ejecutamos el experimento de aguja de Buffon una gran cantidad de veces. Por la ley de grandes números, la proporción de cruces de grietas debe ser aproximadamente la misma que la probabilidad de un cruce de grietas. Más precisamente, vamos a denotar el número de cruces de crack en las primeras\(n\) carreras por\(N_n\). Obsérvese que\(N_n\) es una variable aleatoria para el experimento compuesto que consiste en\(n\) repeticiones del experimento básico con aguja. Así, si\(n\) es grande, deberíamos tener\( \frac{N_n}{n} \approx \frac{2 L}{\pi} \) y por lo tanto\[ \pi \approx \frac{2 L n}{N_n} \] Esta es la famosa estimación de Buffon de\(\pi\). En la simulación del experimento de aguja de Buffon, esta estimación se calcula en cada ejecución y se muestra numéricamente en la segunda tabla y visualmente en una gráfica.
Ejecuta el experimento de la aguja de Buffon con longitudes de aguja\(L \in \{0.3, 0.5, 0.7, 1\}\). En cada caso, observe la estimación de a\(\pi\) medida que se ejecuta la simulación.
Analicemos el problema de estimación con más detenimiento. En cada carrera\(j\) tenemos una variable indicadora\(I_j\), donde\(I_j = 1\) si la aguja cruza una grieta en carrera\(j\) y\(I_j = 0\) si la aguja no cruza una grieta en carrera\(j\). Estas variables indicadoras son independientes e identicamente distribuidas, ya que estamos asumiendo replicaciones independientes del experimento. Así, la secuencia forma un proceso de ensayos de Bernoulli.
El número de cruces de grietas en las primeras\(n\) ejecuciones del experimento es el\[ N_n = \sum_{j=1}^n I_j \] que tiene la distribución binomial con parámetros\(n\) y\(2 L / \pi\).
La media y varianza\(N_n\) de
- \(\E(N_n) = n \frac{2 L}{\pi}\)
- \(\var(N_n) = n \frac{2 L}{\pi} \left(1 - \frac{2 L}{\pi}\right)\)
Con probabilidad 1,\(\frac{N_n}{2 L n} \to \frac{1}{\pi}\) como\(n \to \infty\) y\(\frac{2 L n}{N_n} \to \pi\) como\(n \to \infty\).
Prueba
aEstos resultados se derivan de la fuerte ley de los grandes números.
Así, tenemos dos estimadores básicos:\(\frac{N_n}{2 L n}\) como estimador de\(\frac{1}{\pi}\) y\(\frac{2 L n}{N_n}\) como estimador de\(\pi\). El estimador de\(\frac{1}{\pi}\) tiene varias propiedades estadísticas importantes. En primer lugar, es imparcial ya que el valor esperado del estimador es el parámetro que se estima:
El estimador de\(\frac{1}{\pi}\) es imparcial:\[ \E \left( \frac{N_n}{2 L n} \right) = \frac{1}{\pi} \]
Prueba
Esto se desprende de los resultados anteriores para la distribución binomial y las propiedades de valor esperado.
Dado que este estimador es imparcial, la varianza da el error cuadrático medio:\[ \var \left( \frac{N_n}{2 L n} \right) = \E \left[ \left( \frac{N_n}{2 L n} - \frac{1}{\pi} \right)^2 \right] \]
El error cuadrático medio del estimador de\( \frac{1}{\pi} \) es\[ \var \left( \frac{N_n}{2 L n} \right) = \frac{\pi - 2 L}{2 L n \pi^2} \]
La varianza es una función decreciente de la longitud de la aguja\(L\).
Así, el estimador de\(\frac{1}{\pi}\) mejora a medida que aumenta la longitud de la aguja. Por otro lado, el estimador de\(\pi\) está sesgado; tiende a sobreestimar\(\pi\):
El estimador de\(\pi\) está sesgado positivamente:\[ \E \left( \frac{2 L n}{N_n} \right) \ge \pi \]
Prueba
Usa la desigualdad de Jensen.
El estimador de\(\pi\) también tiende a mejorar a medida que aumenta la longitud de la aguja. Esto no es fácil de ver matemáticamente. No obstante, se puede ver empíricamente.
En el experimento de aguja de Buffon, ejecute la simulación 5000 veces cada una con\(L = 0.3\)\(L = 0.5\),\(L = 0.7\), y\(L = 0.9\). Observe lo bien que parece funcionar el estimador en cada caso.
Por último, debemos señalar que como cuestión práctica, el experimento con aguja de Buffon no es un método muy eficiente de aproximación\(\pi\). Según Richard Durrett, estimar\(\pi\) a cuatro decimales con ¡\(L = \frac{1}{2}\)requeriría alrededor de 100 millones de tiradas!
Ejecute el experimento de la aguja de Buffon hasta que las estimaciones de\(\pi\) parezcan ser consistentemente correctas a dos decimales. Anote el número de corridas requeridas. Pruebe esto para longitudes de aguja\(L = 0.3\)\(L = 0.5\)\(L = 0.7\),,\(L = 0.9\) y compare los resultados.
Muestra cómo simular el ángulo\(X\) y la distancia\(Y\) en el experimento de aguja de Buffon usando números aleatorios.
Contestar
\(X = \pi U\),\(Y = V\), donde\(U\) y\(V\) son números aleatorios.
Notas
El problema de la aguja de Buffon se resuelve esencialmente mediante la integración de Montecarlo. En general, los métodos de Montecarlo utilizan muestreo estadístico para aproximar las soluciones de problemas que son difíciles de resolver analíticamente. La teoría moderna de los métodos de Montecarlo comenzó con Stanislaw Ulam, quien utilizó los métodos sobre problemas asociados con el desarrollo de la bomba de hidrógeno.
El problema original de la aguja se ha extendido de muchas maneras, comenzando por Simon Laplace quien consideró un piso con baldosas rectangulares. En efecto, las variaciones sobre el problema son problemas de investigación activa incluso hoy en día.
Neil Weiss ha señalado que nuestra simulación por computadora del experimento de aguja de Buffon es circular, en el sentido que el programa asume el conocimiento de\(\pi\) (se puede ver esto en el resultado de la simulación anterior).
Intenta escribir un algoritmo informático para el problema de la aguja de Buffon, sin asumir el valor de\(\pi\) ni ningún otro número trascendental.


