11.1: Introducción a los ensayos de Bernoulli
- Page ID
- 151695
Teoría Básica
Definición
El proceso de ensayos de Bernoulli, llamado así por Jacob Bernoulli, es uno de los procesos aleatorios más simples pero más importantes en probabilidad. Esencialmente, el proceso es la abstracción matemática del lanzamiento de monedas, pero debido a su amplia aplicabilidad, generalmente se establece en términos de una secuencia de ensayos
genéricos.
Una secuencia de ensayos de Bernoulli satisface los siguientes supuestos:
- Cada ensayo tiene dos posibles resultados, en el lenguaje de la confiabilidad llamado éxito y fracaso.
- Los juicios son independientes. Intuitivamente, el resultado de un juicio no influye sobre el resultado de otro juicio.
- En cada ensayo, la probabilidad de éxito es\(p\) y la probabilidad de fracaso es\(1 - p\) donde\(p \in [0, 1]\) está el parámetro de éxito del proceso.
Variables aleatorias
Matemáticamente, podemos describir el proceso de ensayos de Bernoulli con una secuencia de variables aleatorias indicadoras:
\[ \bs{X} = (X_1, X_2, \ldots) \]
Una variable indicadora es una variable aleatoria que toma solo los valores 1 y 0, que en esta configuración denotan éxito y fracaso, respectivamente. La variable indicadora\(X_i\) simplemente registra el resultado del juicio\(i\). Así, las variables indicadoras son independientes y tienen la misma función de densidad de probabilidad:\[ \P(X_i = 1) = p, \quad \P(X_i = 0) = 1 - p \] La distribución definida por esta función de densidad de probabilidad se conoce como la distribución de Bernoulli. En términos estadísticos, el proceso de ensayos de Bernoulli corresponde al muestreo de la distribución de Bernoulli. En particular, los primeros\(n\) ensayos\((X_1, X_2, \ldots, X_n)\) forman una muestra aleatoria de tamaño\(n\) de la distribución de Bernoulli. Obsérvese nuevamente que el proceso de ensayos de Bernoulli se caracteriza por un solo parámetro\(p\).
La función conjunta de densidad de probabilidad de\((X_1, X_2, \ldots, X_n)\) los ensayos viene dada por\[ f_n(x_1, x_2, \ldots, x_n) = p^{x_1 + x_2 + \cdots + x_n} (1 - p)^{n- (x_1 + x_2 + \cdots + x_n)}, \quad (x_1, x_2, \ldots, x_n) \in \{0, 1\}^n \]
Prueba
Esto se desprende de los supuestos básicos de independencia y las probabilidades constantes de 1 y 0.
Obsérvese que el exponente de\(p\) en la función de densidad de probabilidad es el número de éxitos en\(n\) los ensayos, mientras que el exponente de\(1 - p\) es el número de fallas.
Si\(\bs{X} = (X_1, X_2, \ldots,)\) es un proceso de ensayos de Bernoulli con parámetro\(p\) entonces\(\bs{1} - \bs{X} = (1 - X_1, 1 - X_2, \ldots)\) es una secuencia de ensayos de Bernoulli con parámetro\(1 - p\).
Supongamos que\(\bs{U} = (U_1, U_2, \ldots)\) es una secuencia de variables aleatorias independientes, cada una con la distribución uniforme en el intervalo\([0, 1]\). Para\(p \in [0, 1]\) y\(i \in \N_+\), vamos\(X_i(p) = \bs{1}(U_i \le p)\). Entonces\(\bs{X}(p) = \left( X_1(p), X_2(p), \ldots \right)\) es un proceso de ensayos de Bernoulli con probabilidad\(p\).
Tenga en cuenta que en el resultado anterior, los procesos de ensayos de Bernoulli para todos los valores posibles del parámetro\(p\) se definen en un espacio de probabilidad común. Este tipo de construcción a veces se conoce como acoplamiento. Este resultado también muestra cómo simular un proceso de ensayos de Bernoulli con números aleatorios. Todos los demás procesos aleatorios estudiados en este capítulo son funciones de la secuencia de ensayos de Bernoulli, y por lo tanto también pueden simularse.
Momentos
Dejar\(X\) ser una variable indciadora con\(\P(X = 1) = p\), donde\(p \in [0, 1]\). Así,\(X\) es el resultado de un ensayo genérico de Bernoulli y tiene la distribución de Bernoulli con parámetro\(p\). Los siguientes resultados dan la media, varianza y algunos de los momentos más altos. Un dato útil es que si tomamos una potencia positiva de una variable indicadora, no pasa nada; es decir,\(X^n = X\) para\(n \gt 0\)
La media y varianza\( X \) de
- \(\E(X) = p\)
- \( \var(X) = p (1 - p) \)
Prueba
- \( \E(X) = 1 \cdot p ( 0 \cdot (1 - p) = p \)
- \( \var(X) = \E\left(X^2\right) - \left[\E(X)\right]^2 = \E(X) - \left[\E(X)\right]^2 = p - p^2 \)
Tenga en cuenta que la gráfica de\( \var(X) \), en función de\( p \in [0, 1] \) es una parábola que se abre hacia abajo. En particular, el valor más grande es\(\frac{1}{4}\) cuándo\(p = \frac{1}{2}\), y el valor más pequeño es 0 cuando\(p = 0\) o\(p = 1\). Por supuesto, en los dos últimos casos,\( X \) es determinista, tomando el único valor 0 cuando\( p = 0 \) y el único valor 1 cuando\( p = 1 \)
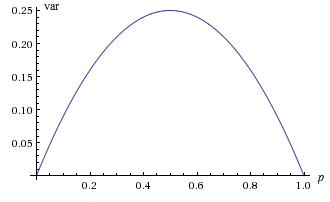
Supongamos que\( p \in (0, 1) \). La asimetría y curtosis\(X\) de
- \(\skw(X) = \frac{1 - 2 p}{\sqrt{p (1 - p)}}\)
- \(\kur(X) = -3 + \frac{1}{p (1 - p)}\)
La función generadora de probabilidad de\(X\) es\( P(t) = \E\left(t^X\right) = (1 - p) + p t \) para\( t \in \R \).
Ejemplos y Aplicaciones
Monedas
Como señalamos anteriormente, el ejemplo más obvio de los juicios de Bernoulli es el lanzamiento de monedas, donde el éxito significa cabezas y el fracaso significa colas. El parámetro\(p\) es la probabilidad de cabezas (por lo que en general, la moneda está sesgada).
En el experimento básico de monedas, set\(n = 100\) y Para cada\(p \in \{0.1, 0.3, 0.5, 0.7, 0.9\}\) ejecutar el experimento y observar los resultados.
Ejemplos Genéricos
En cierto sentido, el ejemplo más general de los ensayos de Bernoulli ocurre cuando se replica un experimento. Específicamente, supongamos que tenemos un experimento aleatorio básico y un evento de interés\(A\). Supongamos ahora que creamos un experimento compuesto que consiste en replicaciones independientes del experimento básico. Definir éxito en el juicio\(i\) para que signifique que el evento\(A\) ocurrió en el\(i\) th run, y definir el fracaso en el juicio\(i\) para significar que el evento\(A\) no ocurrió en el\(i\) th run. Esto define claramente un proceso de ensayos de Bernoulli con parámetro\(p = \P(A)\).
Los ensayos de Bernoulli también se forman cuando se toma una muestra de una población dicotómica. Específicamente, supongamos que tenemos una población de dos tipos de objetos, a los que nos referiremos como tipo 0 y tipo 1. Por ejemplo, los objetos podrían ser personas, clasificadas como masculinas o femeninas, o los objetos podrían ser componentes, clasificados como buenos o defectuosos. Seleccionamos\( n \) objetos al azar de la población; por definición, esto significa que cada objeto de la población en el momento del sorteo es igualmente probable que sea elegido. Si el muestreo es con reemplazo, entonces cada objeto dibujado se reemplaza antes del siguiente sorteo. En este caso, los sorteos sucesivos son independientes, por lo que los tipos de los objetos en la muestra forman una secuencia de ensayos de Bernoulli, en los que el parámetro\(p\) es la proporción de objetos tipo 1 en la población. Si el muestreo es sin reemplazo, entonces los sucesivos sorteos son dependientes, por lo que los tipos de los objetos en la muestra no forman una secuencia de ensayos de Bernoulli. Sin embargo, si el tamaño de la población es grande en comparación con el tamaño de la muestra, la dependencia causada por no reemplazar los objetos puede ser despreciable, por lo que para todos los fines prácticos, los tipos de los objetos en la muestra pueden tratarse como una secuencia de ensayos de Bernoulli. La discusión adicional sobre el muestreo de una población dicotómica se encuentra en el capítulo Modelos de muestreo finito.
Supongamos que un estudiante toma una prueba de opción múltiple. La prueba tiene 10 preguntas, cada una de las cuales tiene 4 respuestas posibles (solo una correcta). Si el alumno adivina ciegamente la respuesta a cada pregunta, ¿las preguntas forman una secuencia de juicios de Bernoulli? Si es así, identificar los resultados del ensayo y el parámetro\(p\).
Contestar
Sí, probablemente así. Los resultados son correctos e incorrectos y\(p = \frac{1}{4}\).
Candidato\(A\) se postula para un cargo en cierto distrito. Se seleccionan al azar a veinte personas de la población de votantes registrados y se les pregunta si prefieren candidato\(A\). ¿Las respuestas forman una secuencia de ensayos de Bernoulli? Si es así, identificar los resultados del ensayo y el significado del parámetro\(p\).
Contestar
Sí, aproximadamente, asumiendo que el número de electores registrados es grande, en comparación con el tamaño muestral de 20. Los resultados son preferidos\(A\) y no prefieren\(A\);\(p\) es la proporción de electores en todo el distrito que prefieren\(A\).
Una rueda de ruleta americana tiene 38 ranuras; 18 son rojas, 18 son negras y 2 son verdes. Un jugador juega a la ruleta 15 veces, apostando al rojo cada vez. ¿Los resultados forman una secuencia de ensayos de Bernoulli? Si es así, identificar los resultados del ensayo y el parámetro\(p\).
Contestar
Sí, los resultados son rojos y negros, y\(p = \frac{18}{38}\).
La ruleta se discute con más detalle en el capítulo sobre Juegos de azar.
Dos tenistas juegan un conjunto de 6 juegos. ¿Los juegos forman una secuencia de pruebas de Bernoulli? Si es así, identificar los resultados del ensayo y el significado del parámetro\(p\).
Contestar
No, probablemente no. Es casi seguro que los juegos dependen, y la victoria probablemente depende de quién está sirviendo y por lo tanto no es constante de un juego a otro.
Confiabilidad
Recordemos que en el modelo estándar de confiabilidad estructural, un sistema está compuesto por\(n\) componentes que operan independientemente entre sí. Dejar\(X_i\) denotar el estado del componente\(i\), donde 1 significa trabajar y 0 significa falla. Si los componentes son todos del mismo tipo, entonces nuestra suposición básica es que el vector de estado\[ \bs{X} = (X_1, X_2, \ldots, X_n) \] es una secuencia de ensayos de Bernoulli. El estado del sistema, (de nuevo donde 1 significa trabajar y 0 significa fallido) depende únicamente de los estados de los componentes, y por lo tanto es una variable aleatoria\[ Y = s(X_1, X_, \ldots, X_n) \] donde\(s: \{0, 1\}^n \to \{0, 1\}\) está la función de estructura. Generalmente, la probabilidad de que un dispositivo esté funcionando es la confiabilidad del dispositivo, por lo que el parámetro\(p\) de la secuencia de ensayos de Bernoulli es la confiabilidad común de los componentes. Por independencia, la confiabilidad del sistema\(r\) es una función de la confiabilidad del componente:\[ r(p) = \P_p(Y = 1), \quad p \in [0, 1] \] donde estamos enfatizando la dependencia de la medida de probabilidad\(\P\) en el parámetro\(p\). Lo suficientemente apropiado, esta función se conoce como la función de confiabilidad. Nuestro reto suele ser encontrar la función de confiabilidad, dada la función de estructura.
Un sistema en serie está funcionando si y solo si cada componente está funcionando.
- El estado del sistema es\(Y = X_1 X_2 \cdots X_n = \min\{X_1, X_2, \ldots, X_n\}\).
- La función de confiabilidad es\(r(p) = p^n\) para\(p \in [0, 1]\).
Un sistema paralelo está funcionando si y solo si al menos un componente está funcionando.
- El estado del sistema es\(Y = 1 - (1 - X_1)(1 - X_2) \cdots (1 - X_n) = \max\{X_1, X_2, \ldots, X_n\}\).
- La función de confiabilidad es\(r(p) - 1 - (1 - p)^n\) para\(p \in [0, 1]\).
Recordemos que en algunos casos, el sistema puede representarse como una gráfica o red. Los bordes representan los componentes y los vértices las conexiones entre los componentes. El sistema funciona si y sólo si hay una ruta de trabajo entre dos vértices designados, que denotaremos por\(a\) y\(b\).
Encuentre la confiabilidad de la red de puentes Wheatstone que se muestra a continuación (llamada así por Charles Wheatstone).
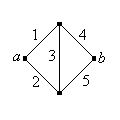
Contestar
\(r(p) = p \, (2 \, p - p^2)^2 + (1 - p)(2 \, p^2 - p^4)\)
El análisis de sangre agrupada
Supongamos que cada persona en una población, independientemente de todas las demás, tiene una determinada enfermedad con probabilidad\(p \in (0, 1)\). Así, con respecto a la enfermedad, las personas de la población forman una secuencia de ensayos de Bernoulli. La enfermedad se puede identificar mediante un análisis de sangre, pero por supuesto la prueba tiene un costo.
Para un grupo de\(k\) personas, compararemos dos estrategias. El primero es poner a prueba a las\(k\) personas de manera individual, para que por supuesto, se requieran\(k\) pruebas. La segunda estrategia es juntar las muestras de sangre de las\(k\) personas y analizar primero la muestra agrupada. Suponemos que la prueba es negativa si y sólo si todas\(k\) las personas están libres de la enfermedad; en este caso solo se requiere una prueba. Por otra parte, la prueba es positiva si y sólo si al menos una persona tiene la enfermedad, en cuyo caso entonces tenemos que probar a las personas individualmente; en este caso se requieren\(k + 1\) pruebas. Así, vamos a\(Y\) denotar el número de pruebas requeridas para la estrategia agrupada.
El número de pruebas\(Y\) tiene las siguientes propiedades:
- \(\P(Y = 1) = (1 - p)^k, \quad \P(Y = k + 1) = 1 - (1 - p)^k\)
- \(\E(Y) = 1 + k \left[1 - (1 - p)^k\right]\)
- \(\var(Y) = k^2 (1 - p)^k \left[1 - (1 - p)^k\right]\)
En términos de valor esperado, la estrategia agrupada es mejor que la estrategia básica si y solo si\[ p \lt 1 - \left( \frac{1}{k} \right)^{1/k} \]
La gráfica del valor\(p_k = 1 - (1 / k)^{1/k}\) crítico en función de\(k \in [2, 20]\) se muestra en la siguiente gráfica:
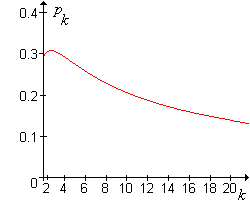
El valor crítico\(p_k\) satisface las siguientes propiedades:
- El valor máximo de\(p_k\) ocurre en\(k = 3\) y\(p_3 \approx 0.307\).
- \(p_k \to 0\)como\(k \to \infty\).
De ello se deduce que si\(p \ge 0.307\), el agrupamiento nunca tiene sentido, independientemente del tamaño del grupo\(k\). En el otro extremo, si\(p\) es muy pequeño, por lo que la enfermedad es bastante rara, la agrupación es mejor a menos que el tamaño del grupo\(k\) sea muy grande.
Ahora supongamos que tenemos\(n\) personas. Si\(k \mid n\) entonces podemos dividir la población en\(n / k\) grupos de\(k\) cada uno, y aplicar la estrategia agrupada a cada grupo. Nótese que\(k = 1\) corresponde a pruebas individuales, y\(k = n\) corresponde a la estrategia agrupada en toda la población. Dejar\(Y_i\) denotar el número de pruebas requeridas para el grupo\(i\).
Las variables aleatorias\((Y_1, Y_2, \ldots, Y_{n/k})\) son independientes y cada una tiene la distribución dada anteriormente.
El número total de pruebas requeridas para este esquema de partición es\(Z_{n,k} = Y_1 + Y_2 + \cdots + Y_{n/k}\).
El número total esperado de pruebas es\[ \E(Z_{n,k}) = \begin{cases} n, & k = 1 \\ n \left[ \left(1 + \frac{1}{k} \right) - (1 - p)^k \right], & k \gt 1 \end{cases} \]
La varianza del número total de pruebas es\[ \var(Z_{n,}) = \begin{cases} 0, & k = 1 \\ n \, k \, (1 - p)^k \left[ 1 - (1 - p)^k \right], & k \gt 1 \end{cases} \]
Así, en términos de valor esperado, la estrategia óptima es agrupar a la población en\(n / k\) grupos de tamaño\(k\), donde\(k\) minimiza la función de valor esperado arriba. Es difícil obtener una expresión de forma cerrada para el valor óptimo de\(k\), pero este valor se puede determinar numéricamente para específico\(n\) y\(p\).
Para los siguientes valores de\(n\) y\(p\), encuentre el tamaño óptimo de agrupación\(k\) y el número esperado de pruebas. (Restringir su atención a valores de\(k\) esa división\(n\).)
- \(n = 100\),\(p = 0.01\)
- \(n = 1000\),\(p = 0.05\)
- \(n = 1000\),\(p = 0.001\)
Contestar
- \(k = 10\),\(\E(Y_k) = 19.56\)
- \(k = 5\),\(\E(Y_k) = 426.22\)
- \(k = 40\),\(\E(Y_k) = 64.23\)
Si\(k\) no se divide\(n\), entonces podríamos dividir la población de\(n\) personas en\(\lfloor n / k \rfloor\) grupos de\(k\) cada uno y un grupo restante
con\(n \mod k\) miembros. Esto complica claramente el análisis, pero no introduce ninguna idea nueva, por lo que dejaremos esta extensión al lector interesado.


