13.11: Estrategias Óptimas
- Page ID
- 152143
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Teoría Básica
Definiciones
Recordemos que la regla de parada para el rojo y el negro es seguir jugando hasta que el jugador se arruine o su fortuna llegue a la fortuna objetivo\(a\). Así, la estrategia de la jugadora es decidir cuánto apostar en cada juego antes de que deba detenerse. Supongamos que tenemos una clase de estrategias que corresponden a ciertas fortunas y apuestas válidas;\(A\) denotará el conjunto de fortunas y\(B_x\) denotará el conjunto de apuestas válidas para\(x \in A\). Por ejemplo, a veces (como con el juego tímido) podríamos querer restringir las fortunas al conjunto de enteros\(\{0, 1, \ldots, a\}\); otras veces (como con el juego en negrita) podríamos querer usar el intervalo\([0, 1]\) como el espacio de la fortuna. En cuanto a las apuestas, recordemos que la jugadora no puede apostar lo que no tiene y no apostará más de lo que necesita para alcanzar el objetivo. Así, una función de apuestas\(S\) debe satisfacer\[ S(x) \le \min\{x, a - x\}, \quad x \in A \] Además, siempre restringimos nuestras estrategias a aquellas para las que el tiempo de parada\(N\) es finito.
La función de éxito de una estrategia es la probabilidad de que el jugador alcance el objetivo\(a\) con esa estrategia, en función de la fortuna inicial\(x\). Una estrategia con función de éxito\(V\) es óptima si para cualquier otra estrategia con función de éxito\(U\), tenemos\(U(x) \le V(x)\) para\(x \in A\).
Si existe una estrategia óptima, entonces la función de éxito óptima es única.
Sin embargo, puede no existir una estrategia óptima o puede haber varias estrategias óptimas. Además, la cuestión de la optimalidad depende del valor de la probabilidad de ganar el juego\(p\), además de la estructura de fortunas y apuestas.
Una Condición para la Óptima
Nuestro teorema principal da una condición para la optimalidad:
Una estrategia\(S\) con función de éxito\(V\) es óptima si\[ p V(x + y) + q V(x - y) \le V(x); \quad x \in A, \, y \in B_x \]
Prueba
Considera la siguiente estrategia: si la fortuna inicial es\(x \in A\), escogemos\(y \in A_x\) y luego apostamos por\(y\) el primer juego; a partir de entonces seguimos la estrategia\(S\). Acondicionamiento al resultado del primer juego, la función de éxito para esta nueva estrategia es\[ U(x) = p\,V(x + y) + q\,V(x - y) \] Así, el teorema se puede replantear de la siguiente manera: Si\(S\) es óptimo con respecto a la clase de estrategias que acabamos de describir, entonces\(S\) es óptimo sobre todas las estrategias. Que\(T\) sea una estrategia arbitraria con función de éxito\(U\). La variable aleatoria\(V(X_n)\) puede interpretarse como la probabilidad de ganar si la estrategia del jugador es reemplazada por estrategia\(S\) después del tiempo\(n\). Acondicionar el resultado del juego\(n\) da\[ \E[V(X_n) \mid X_0 = x] = \E[p \, V(X_{n-1} + Y_n) + q \, V(X_{n-1} - Y_n) \mid X_0 = x] \] Usar la condición de optimalidad da\[ \E[V(X_n) \mid X_0 = x] \le \E[V(X_{n-1}) \mid X_0 = x] , \quad n \in \N_+, \; x \in A \] Si sigue eso\(\E[V(X_n) \mid X_0 = x] \le V(x)\) para\(n \in \N_+\) y\(x \in A\). Ahora vamos a\(N\) denotar el tiempo de parada para la estrategia\(T\). Dejando que\(n \to \infty\) tengamos\(\E[V(X_N) \mid X_0 = x] \le V(x)\) para\(x \in A\). Pero\(\E[V(X_N) \mid X_0 = x] = U(x)\) para\(x \in A\). Así\(U(x) \le V(x)\) para\(x \in A\).
Juicios favorables con una apuesta mínima
Supongamos\(p \ge \frac{1}{2}\) ahora que para que los juicios sean favorables (o al menos no injustos) para el jugador. A continuación, supongamos que todas las apuestas deben ser múltiplos de una unidad básica, lo que bien podríamos suponer que es $1. Por supuesto, las casas de juego reales tienen esta restricción. Así el conjunto de fortunas válidas es\(A = \{0, 1, \ldots, a\}\) y el conjunto de apuestas válidas para\(x \in A\) es\(B_x = \{0, 1, \ldots, \min\{x, a - x\}\}\). Nuestro principal resultado para este caso es
El juego tímido es una estrategia óptima.
Prueba
Recordar la función de éxito\(f\) para el juego tímido y recordar la condición de optimalidad. Esta condición se mantiene si\(p = \frac{1}{2}\). Si\(p \gt \frac{1}{2}\), la condición para la optimalidad es equivalente a\[ p \left(\frac{q}{p}\right)^{x+y} + q \left(\frac{q}{p}\right)^{x-y} \ge \left(\frac{q}{p}\right)^x \] Pero esta condición es equivalente a la\(p q \left(p^y - q^y\right)\left(p^{y - 1} - q^{y - 1}\right) \le 0\) que se sostiene claramente si\(p \gt \frac{1}{2}\).
En el juego rojo y negro fijó la fortuna objetivo en 16, la fortuna inicial en 8, y la probabilidad de ganar juego en 0.45. Define la estrategia de su elección y juegue 100 juegos. Compara tu frecuencia relativa de victorias con la probabilidad de ganar con un juego tímido.
Juicios favorables sin una apuesta mínima
Ahora vamos a suponer que la casa permite apuestas arbitrariamente pequeñas y eso\(p \gt \frac{1}{2}\), para que los juicios sean estrictamente favorables. En este caso es natural tomar el objetivo como la unidad monetaria para que el conjunto de fortunas sea\(A = [0, 1]\), y el conjunto de apuestas para\(x \in A\) es\(B_x = [0, \min\{x, 1 - x\}]\). Nuestro principal resultado para este caso se da a continuación. Los resultados para el juego tímido jugarán un papel importante en el análisis, por lo que dejaremos\(f(j, a)\) denotar la probabilidad de alcanzar un objetivo entero\(a\), comenzando en el entero\(j \in [0, a]\), con apuestas unitarias.
La función óptima de éxito es\(V(x) = x\) para\(x \in (0, 1]\).
Prueba
Arreglar una fortuna inicial racional\(x = \frac{k}{n} \in [0, 1]\). \(m\)Sea un entero positivo y supongamos que, a partir de\(x\), el jugador\(\frac{1}{m n}\) apuesta por cada juego. Esta estrategia equivale a un juego tímido con la fortuna objetivo\(m n\), y la fortuna inicial\(m k\). De ahí que la probabilidad de alcanzar el objetivo 1 bajo esta estrategia es\(f(m k, m n)\). Pero\(f(m k, m n) \to 1\) como\(m \to \infty\). De ello se deduce que\(V(x) = x\) si\(x \in (0, 1]\) es racional. Pero\(V\) está aumentando así\(V(x) = x\) para todos\(x \in (0, 1]\)
Juicios injustos
Ahora vamos a suponer que\(p \le \frac{1}{2}\) para que los juicios sean injustos, o al menos no favorables. Como antes, tomaremos la fortuna objetivo como unidad monetaria básica y permitiremos cualquier fracción válida de esta unidad como apuesta. Así, el conjunto de fortunas es\(A = [0, 1]\), y el conjunto de apuestas para\(x \in A\) es\(B_x = [0, \min\{x, 1 - x\}]\). Nuestro principal resultado para este caso es
El juego atrevido es óptimo.
Prueba
Dejar\(F\) denotar la función de éxito para el juego en negrita, y dejar\[ D(x, y) = F \left(\frac{x + y}{2}\right) - [p F(x) + q F(y)] \] La condición de optimalidad equivalente a\(D(x, y) \le 0\) for\(0 \le x \le y \le 1\). A partir de la continuidad de\(F\), basta con probar esta desigualdad cuando\(x\) y\(y\) son racionales binarios. Es sencillo ver que\(D(x, y) \le 0\) cuando\(x\) y\(y\) tener rango 0:\(x = 0\),\(y = 0\) o\(x = 0\),\(y = 1\) o\(x = 1\),\(y = 1\). Supongamos ahora que\(D(x, y) \le 0\) cuando\(x\) y\(y\) tener rango\(m\) o menos. Tenemos los siguientes casos:
- Si\(x \le y \le \frac{1}{2}\) entonces\(D(x, y) = p D(2 x, 2 y)\).
- Si\(\frac{1}{2} \le x \le y\) entonces\(D(x, y) = q D(2 x - 1, 2 y - 1)\).
- Si\(x \le \frac{x + y}{2} \le \frac{1}{2} \le y\) y\(2 y - 1 \le 2 x\) entonces\(D(x, y) = (q - p) F(2 y - 1) + q D(2 y - 1, 2 x)\).
- Si\(x \le \frac{x + y}{2} \le \frac{1}{2} \le y\) y\(2 x \le 2 y - 1\) entonces\(D(x, y) = (q - p) F(2 x) + q D(2 x, 2 y - 1)\).
- Si\(x \le \frac{1}{2} \le \frac{x + y}{2} \le y\) y\(2 y - 1 \le 2 x\) entonces\(D(x, y) = p (q - p) [1 - F(2 x)] + p D(2 y - 1, 2 x)\).
- Si\(x \le \frac{1}{2} \le \frac{x + y}{2} \le y\) y\(2 x \le 2 y - 1\) entonces\(D(x, y) = p (q - p) [1 - F(2 y - 1)] + p D(2 x, 2 y - 1)\).
La hipótesis de inducción ahora se puede aplicar a cada caso para terminar la prueba.
En el juego rojo y negro, fijó la fortuna objetivo en 16, la fortuna inicial en 8, y la probabilidad de ganar el juego en 0.45. Define la estrategia de su elección y juegue 100 juegos. Compara tu frecuencia relativa de victorias con la probabilidad de ganar con juego negrita.
Otras Estrategias Óptimas en el Caso Subjusto
Consideremos nuevamente el caso sub-justo donde\(p \le \frac{1}{2}\) para que los juicios no sean favorables para el jugador. Mostraremos que el juego audaz no es la única estrategia óptima; asombrosamente, hay infinitamente muchas estrategias óptimas. Recordemos primero que la estrategia audaz tiene función de apuestas\[ S_1(x) = \min\{x, 1 - x\} = \begin{cases} x, & 0 \le x \le \frac{1}{2} \\ 1 - x, & \frac{1}{2} \le x \le 1 \end{cases} \]
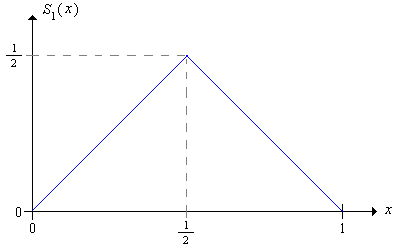
Consideremos la siguiente estrategia, a la que nos referiremos como la estrategia audaz de segundo orden:
- Con fortuna\(x \in \left(0, \frac{1}{2}\right)\), juega audazmente con el objeto de alcanzar\(\frac{1}{2}\) antes de caer a 0.
- Con fortuna\(x \in \left(\frac{1}{2}, 1\right)\), juega audazmente con el objeto de llegar a 1 sin caer por debajo\(\frac{1}{2}\).
- Con fortuna\(\frac{1}{2}\), juega con valentía y apuesta\(\frac{1}{2}\)
La estrategia audaz de segundo orden tiene función de apuestas\(S_2\) dada por\[ S_2(x) = \begin{cases} x, & 0 \le x \lt \frac{1}{4} \\ \frac{1}{2} - x, & \frac{1}{4} \le x \lt \frac{1}{2} \\ \frac{1}{2}, & x = \frac{1}{2} \\ x - \frac{1}{2}, & \frac{1}{2} \lt x \le \frac{3}{4} \\ 1 - x, & \frac{3}{4} \lt x \le 1 \end{cases} \]
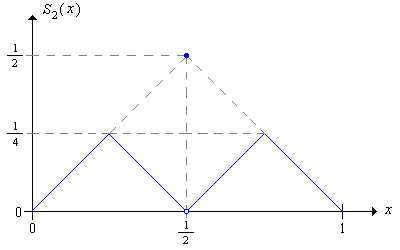
La estrategia audaz de segundo orden es óptima.
Prueba
Vamos a\(F_2\) denotar la función de éxito asociada a la estrategia\(S_2\). Supongamos primero que el jugador comienza con la fortuna\(x \in (0, \frac{1}{2})\) bajo estrategia\(S_2\). Tenga en cuenta que el jugador alcanza el objetivo 1 si y solo si alcanza\(\frac{1}{2}\) y luego gana el juego final. Considera la secuencia de fortunas hasta que el jugador llegue a 0 o\(\frac{1}{2}\). Si doblamos las fortunas, entonces tenemos la secuencia de la fortuna bajo la estrategia atrevida ordinaria, comenzando en\(2\,x\) y terminando en 0 o 1. Así se deduce que\[ F_2(x) = p F(2 x), \quad 0 \lt x \lt \frac{1}{2} \] Supongamos a continuación que el jugador inicia con fortuna\(x \in (\frac{1}{2}, 1)\) bajo estrategia\(S_2\). Tenga en cuenta que el jugador alcanza el objetivo 1 si y solo si llega a 1 sin caer de nuevo\(\frac{1}{2}\) o vuelve a caer\(\frac{1}{2}\) y luego gana el juego final. Considera la secuencia de fortunas hasta que el jugador alcance\(\frac{1}{2}\) o 1. Si doblamos las fortunas y restamos 1, entonces tenemos la secuencia de fortuna bajo la estrategia atrevida ordinaria, comenzando en\(2 x - 1\) y terminando en 0 o 1. De esta manera se deduce que\[ F_2(x) = F(2 x - 1) + [1 - F(2 x - 2)] p = p + q F(2 x - 1), \quad \frac{1}{2} \lt x \lt 1 \] Pero ahora, usando la ecuación funcional para el juego negrita ordinario, tenemos\(F_2(x) = F(x)\) para todos\(x \in (0, 1]\), y por lo tanto\(S_2\) es óptimo.
Una vez que entendemos cómo se hace esta construcción, es sencillo definir la estrategia audaz de tercer orden y demostrar que también es óptima.
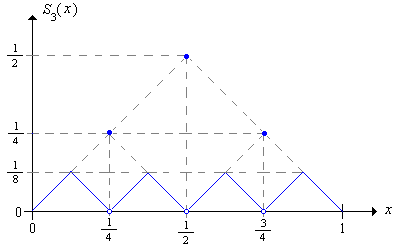
Dar explícitamente la función de apuestas de tercer orden y mostrar que la estrategia es óptima.
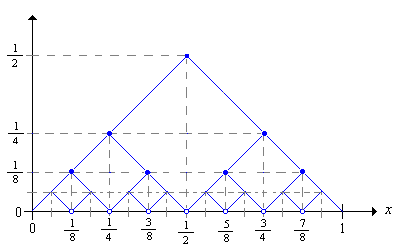
De manera más general, podemos definir la estrategia audaz de orden\(n\) th y demostrar que también es óptima.
La secuencia de estrategias en negrita se puede definir recursivamente a partir de la estrategia básica en negrita de la\(S_1\) siguiente manera:
\[ S_{n+1}(x) = \begin{cases} \frac{1}{2} S_n(2 x), & 0 \le x \lt \frac{1}{2} \\ \frac{1}{2}, & x = \frac{1}{2} \\ \frac{1}{2} S_n(2 x - 1), & \frac{1}{2} \lt x \le 1 \end{cases} \]\(S_n\)es óptimo para cada uno\(n\).
Aún más generalmente, podemos definir una estrategia\(T\) óptima de la siguiente manera: para cada\(x \in [0, 1]\) select\(n_x \in \N_+\) y let\(T(x) = S_{n_x}(x)\). La gráfica a continuación muestra algunas de las gráficas de las estrategias audaces. Para una estrategia óptima\(T\), sólo tenemos que seleccionar, para cada\(x\) una una apuesta en una de las gráficas.
Martingales
Volvamos a la formulación sin escala del rojo y el negro, donde está la fortuna objetivo\( a \in (0, \infty) \) y la fortuna inicial está\( x \in (0, a) \). En el caso de subferia, cuando\( p \le \frac{1}{2} \), ninguna estrategia puede hacerlo mejor que las estrategias óptimas, de manera que la probabilidad de ganar está delimitada por\( x / a \) (con igualdad cuando\( p = \frac{1}{2} \)). Otra prueba elegante de ello se da en la sección sobre desigualdades en el capítulo sobre martingales.


