17.2: Inmuebles y Construcciones
- Page ID
- 151835
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Teoría Básica
Preliminares
Al igual que en la Introducción, comenzamos con un proceso estocástico\( \bs{X} = \{X_t: t \in T\} \) en un espacio de probabilidad subyacente\( (\Omega, \mathscr{F}, \P) \), teniendo espacio de estado\( \R \), y donde el conjunto de índices\( T \) (que representa el tiempo) es\( \N \) (tiempo discreto) o\( [0, \infty) \) (tiempo continuo). A continuación, tenemos una filtración\(\mathfrak{F} = \{\mathscr{F}_t: t \in T\} \), y asumimos que\( \bs{X} \) se adapta a\( \mathfrak{F} \). Así\( \mathfrak{F} \) es una familia cada vez mayor de sub\( \sigma \) -álgebras de\( \mathscr{F} \) y\( X_t \) es medible con respecto a\( \mathscr{F}_t \) for\( t \in T \). Pensamos en\( \mathscr{F}_t \) ello como la colección de eventos hasta el momento\( t \in T \). Suponemos que\( \E\left(\left|X_t\right|\right) \lt \infty \), para que la media de\( X_t \) exista como número real, para cada uno\( t \in T \). Finalmente, en tiempo continuo donde\( T = [0, \infty) \), hacemos los supuestos estándar que\( \bs X \) es correcto continuo y tiene límites izquierdos, y que la filtración\( \mathfrak F \) es correcta continua y completa. Por favor, recuerde lo siguiente de la Introducción:
Definiciones
- \( \bs X \)es una martingala con respecto a\( \mathfrak F \) si\( \E(X_t \mid \mathscr{F}_s) = X_s \) para todos\( s, \, t \in T \) con\( s \le t \).
- \( \bs X \)es una sub-martingala con respecto a\( \mathfrak F \) si\( \E(X_t \mid \mathscr{F}_s) \ge X_s \) para todos\( s, \, t \in T \) con\( s \le t \).
- \( \bs X \)es una super-martingala con respecto a\( \mathfrak F \) si\( \E(X_t \mid \mathscr{F}_s) \le X_s \) para todos\( s, \, t \in T \) con\( s \le t \).
Nuestro objetivo en esta sección es dar una serie de propiedades básicas de las martingales y dar formas de construir martingales a partir de otro tipo de procesos. Los teoremas más profundos y fundamentales se estudiarán en las siguientes secciones.
Propiedades Básicas
Nuestro primer resultado es que la propiedad martingala se conserva bajo una filtración más basta.
Supongamos que el proceso\( \bs X \) y la filtración\( \mathfrak F \) satisfacen los supuestos básicos anteriores y que\( \mathfrak G \) es una filtración más basta que\( \mathscr{G}_t \subseteq \mathscr{F}_t \) para\( \mathfrak F \) eso para\( t \in T \). Si\( \bs X \) es una martingala (sub-martingala, super-martingala) con respecto a\( \mathfrak F \) y\( \bs X \) se adapta a\( \mathfrak G \) entonces\( \bs X \) es una martingala (sub-martingala, super-martingala) con respecto a\( \mathfrak G \).
Prueba
Supongamos que\( s, \, t \in T \) con\( s \le t \). La prueba utiliza la torre y aumentando las propiedades de valor esperado condicional, y el hecho de que\( \bs X \) se adapte a\( \mathfrak G \)
- Si\( \bs X \) es una martingala con respecto a\( \mathfrak F \) entonces\[ \E(X_t \mid \mathscr{G}_s) = \E\left[\E(X_t \mid \mathscr{F}_s) \mid \mathscr{G}_s\right] = \E(X_s \mid \mathscr{G}_s) = X_s \]
- Si\( \bs X \) es un sub-martinagle con respecto a\( \mathfrak F \) entonces\[ \E(X_t \mid \mathscr{G}_s) = \E\left[\E(X_t \mid \mathscr{F}_s) \mid \mathscr{G}_s\right] \ge \E(X_s \mid \mathscr{G}_s) = X_s \]
- Si\( \bs X \) es un super-martinagle con respecto a\( \mathfrak F \) entonces\[ \E(X_t \mid \mathscr{G}_s) = \E\left[\E(X_t \mid \mathscr{F}_s) \mid \mathscr{G}_s\right] \le \E(X_s \mid \mathscr{G}_s) = X_s \]
En particular, si\( \bs{X} \) es una martingala (sub-martingala, super-martingala) con respecto a alguna filtración, entonces es una martingala (sub-martingala, super-martingala) con respecto a su propia filtración natural.
Las relaciones que definen martingales, sub-martingales y super-martingales se mantienen para los valores esperados ordinarios (incondicionales). Tuvimos este resultado en la última sección, pero vale la pena repetirlo.
Supongamos que\( s, \, t \in T \) con\( s \le t \).
- Si\( \bs{X} \) es una martingala con respecto a\( \frak{F} \) entonces\( \E(X_s) = \E(X_t) \).
- Si\( \bs{X} \) es una sub-martingala con respecto a\( \frak{F} \) entonces\( \E(X_s) \le \E(X_t) \).
- Si\( \bs{X} \) es una super-martingala con respecto a\( \frak{F} \) entonces\( \E(X_s) \ge \E(X_t) \).
Prueba
Los resultados se derivan directamente de las definiciones, y el hecho crítico de que\( \E\left[\E\left(X_t \mid \mathscr{F}_s\right)\right] = \E(X_t) \) para\( s, \, t \in T \).
Entonces si\( \bs X \) es una martingala entonces\( \bs X \) tiene valor esperado constante, y este valor es referido como la media de\( \bs X \). Las propiedades martingales se conservan bajo sumas de los procesos estocásticos.
Para los procesos\( \bs{X} = \{X_t: t \in T\} \) y\( \bs{Y} = \{Y_t: t \in T\} \), vamos\( \bs{X} + \bs{Y} = \{X_t + Y_t: t \in T\} \). Si\( \bs X \) y\( \bs Y \) son martingales (sub-martingales, super-martinagles) con respecto a\( \mathfrak F \) entonces\( \bs X + \bs Y \) es una martingala (sub-martingala, super-martinagle) con respecto a\( \mathfrak F \).
Prueba
Los resultados siguen fácilmente a partir de propiedades básicas de valor esperado y valor esperado condicional. Primero tenga en cuenta que\( \E\left(\left|X_t + Y_t\right|\right) \le \E\left(\left|X_t\right|\right) + \E\left(\left|Y_t\right|\right) \lt \infty \) para\( t \in T \). Siguiente\( \E(X_t + Y_t \mid \mathscr{F}_s) = \E(X_t \mid \mathscr{F}_s) + \E(Y_t \mid \mathscr{F}_s)\) para\( s, \, t \in T \) con\( s \le t \).
Las propiedades de sub-martingala y super-martingala se conservan bajo multiplicación por una constante positiva y se invierten bajo multiplicación por una constante negativa.
Para el proceso\( \bs{X} = \{X_t: t \in T\} \) y la constante\( c \in \R \), vamos\( c \bs{X} = \{c X_t: t \in T\} \).
- Si\( \bs X \) es una martingala con respecto a\( \mathfrak F \) entonces también\( c \bs X \) es una martingala con respecto a\( \mathfrak F \)
- Si\( \bs X \) es una sub-martingala con respecto a\( \mathfrak F \), entonces\(c \bs X \) es una sub-martingala si\( c \gt 0 \), una super-martingala si\( c \lt 0 \), y una martingala si\( c = 0 \).
- Si\( \bs X \) es una super-martingala con respecto a\( \mathfrak F \), entonces\(c \bs X \) es una super-martingala si\( c \gt 0 \), una sub-martingala si\( c \lt 0 \), y una martingala si\( c = 0 \).
Prueba
Los resultados siguen fácilmente a partir de propiedades básicas de valor esperado y valor esperado condicional. Primero tenga en cuenta que\( \E\left(\left|c X_t \right|\right) = |c| \E\left(\left|X_t\right|\right) \lt \infty \) para\( t \in T \). Siguiente\( \E(c X_t \mid \mathscr{F}_s) = c \E(X_t \mid \mathscr{F}_s) \) para\( s, \, t \in T \) con\( s \le t \).
La propiedad (a), junto con la propiedad aditiva anterior, significa que la recolección de martingales con respecto a una filtración fija\( \mathfrak F \) forma un espacio vectorial. Aquí hay una clase de transformaciones que convierte a las martingales en sub-martingales.
Supongamos que\( \bs X \) toma valores en un intervalo\( S \subseteq \R \) y que\( g: S \to \R \) es convexo con\( \E\left[\left|g(X_t)\right|\right] \lt \infty \) for\( t \in T \). Si alguna de las siguientes condiciones se mantiene entonces\( g(\bs X) = \{g(X_t): t \in T\} \) es una sub-martingala con respecto a\( \mathfrak F \):
- \( \bs X \)es una martingala.
- \( \bs X \)es una sub-martingala y también\( g \) va en aumento.
Prueba
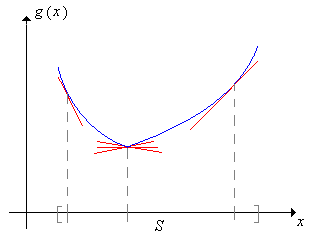
Aquí está el caso especial más importante del resultado anterior:
Supongamos nuevamente que\( \bs X \) es una martingala con respecto a\( \mathfrak F \). Dejemos\( k \in [1, \infty) \) y supongamos que\( \E\left(|X_t|^k\right) \lt \infty \) para\( t \in T \). Entonces el proceso\( |\bs X|^k = \left\{\left|X_t\right|^k: t \in T\right\} \) es una sub-martingala con respecto a\( \mathfrak F \)
Prueba
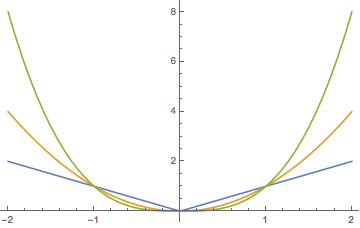
En particular, si\( \bs X \) es una martingala relativa a\( \mathfrak F \) entonces\( |\bs X| = \{|X_t|: t \in T\} \) es una sub-martingala relativa a\( \mathfrak F \). Aquí hay un resultado relacionado que necesitaremos más adelante. Primero recordemos que las partes positivas y negativas de\( x \in \R \) son\( x^+ = \max\{x, 0\} \) y\( x^- = \max\{-x, 0\} \), de modo que\( x^+ \ge 0 \),\( x^- \ge 0 \),\( x = x^+ - x^- \), y\( |x| = x^+ + x^- \).

Si\( \bs X = \{X_t: t \in T\} \) es una sub-martingala relativa a\( \mathfrak F = \{\mathscr{F}_t: t \in T\}\) entonces también\( \bs{X}^+ = \{X_t^+: t \in T\} \) es una sub-martingala relativa a\( \mathfrak F \).
Prueba
Como se muestra en la gráfica anterior, la función\( x \mapsto x^+ \) es creciente y convexa en\( \R \).
Nuestro último resultado de esta discusión es que si tomamos muestras de una martingala de tiempo continuo en una secuencia creciente de puntos de tiempo, obtenemos una martingala de tiempo discreto.
Supongamos nuevamente que el proceso\( \bs X = \{X_t: t \in [0, \infty)\} \) y la filtración\( \mathfrak F = \{\mathscr{F}_t: t \in [0, \infty)\} \) satisfacen los supuestos básicos anteriores. Supongamos también que\( \{t_n: n \in \N\} \subset [0, \infty) \) es una secuencia estrictamente creciente de puntos de tiempo con\( t_0 = 0 \), y definir\( Y_n = X_{t_n} \) y\( \mathscr{G}_n = \mathscr{F}_{t_n} \) para\( n \in \N \). Si\( \bs X \) es una martingala (sub-martingala, super-martingala) con respecto a\( \mathfrak F \) entonces\( \bs Y = \{Y_n: n \in \N\} \) es una martingala (sub-martingala, super-martingala) con respecto a\( \mathfrak G \).
Prueba
Dado que los puntos de tiempo van en aumento, está claro que\( \mathfrak G \) es una filtración de tiempo discreto. A continuación,\( \E(|Y_n|) = \E\left(\left|X_{t_n}\right|\right) \lt \infty \). Por último, supongamos que\( \bs X \) es una martingala y\( n, \, k \in \N \) con\( k \lt n \). Entonces\( t_k \lt t_n \) así\[ \E(Y_n \mid \mathscr{G}_k) = \E\left(X_{t_n} \mid \mathscr{F}_{t_k}\right) = X_{t_k} = Y_k \] De ahí también\( \bs Y \) es una martingala. Las pruebas para sub y super-martingales son similares, pero con desigualdades que reemplazan a la segunda igualdad.
Este resultado suele ser útil para extender pruebas de teoremas en tiempo discreto a tiempo continuo.
La transformación de la martingala
Nuestra siguiente discusión, en tiempo discreto, muestra cómo construir una nueva martingala a partir de una martingala existente y un proceso predecible. Esta construcción resulta muy útil, y tiene una interesante interpretación de juego. Para revisar la definición, recuerde que\( \{Y_n: n \in \N_+\} \) es predecible en relación con la filtración\( \mathfrak F = \{\mathscr{F}_n: n \in \N\} \) si\( Y_n\) es medible con respecto a\(\mathscr{F}_{n-1} \) for\( n \in \N_+ \). Piense en\( Y_n \) como la apuesta que hace un jugador en el juego\( n \in \N_+ \). El jugador puede basar la apuesta en toda la información que tenga en ese momento, incluyendo los resultados de los\( n - 1 \) juegos anteriores. Es decir, puede basar la apuesta en la información codificada en\( \mathscr{F}_{n-1} \).
Supongamos que\( \bs X = \{X_n: n \in \N\} \) se adapta a la filtración\( \mathfrak F = \{\mathscr{F}_n: n \in \N\} \) y que\( \bs Y = \{Y_n: n \in \N_+\} \) es predecible en relación con\( \mathfrak F \). La transformación de\( \bs X \) by\( \bs Y \) es el proceso\( \bs Y \cdot \bs X \) definido por\[ (\bs Y \cdot \bs X)_n = X_0 + \sum_{k=1}^n Y_k (X_k - X_{k-1}), \quad n \in \N \]
El ejemplo motivador detrás del transfrom, en términos de un jugador haciendo una secuencia de apuestas, se da en un ejemplo a continuación. Tenga en cuenta que también\( \bs Y \cdot \bs X \) se adapta a\( \mathfrak F \). Tenga en cuenta también que la transformación depende de\( \bs X \) sólo a través\( X_0 \) y\( \{X_n - X_{n-1}: n \in \N_+\} \). Si\( \bs X \) es una martingala, esta secuencia es la secuencia de diferencia martingala estudiada Introducción.
Supongamos que\( \bs X = \{X_n: n \in \N\} \) se adapta a la filtración\( \mathfrak F = \{\mathscr{F}_n: n \in \N\} \) y que\( \bs{Y} = \{Y_n: n \in \N\} \) es un proceso acotado, predecible en relación con\( \mathfrak{F} \).
- Si\( \bs X \) es una martingala relativa a\( \mathfrak F \) entonces también\( \bs Y \cdot \bs X \) es una martingala relativa a\( \mathfrak F \).
- Si\( \bs X \) es un sub-martingala relativo a\( \mathfrak F \) y no\( \bs Y \) es negativo, entonces también\( \bs Y \cdot \bs X \) es una sub-martingala relativa a\( \mathfrak F \).
- Si\( \bs X \) es un super-martingala relativo a\( \mathfrak F \) y no\( \bs Y \) es negativo, entonces también\( \bs Y \cdot \bs X \) es una super-martingala relativo a\( \mathfrak F \).
Prueba
Supongamos que\( |Y_n| \le c \) para\( n \in \N \) donde\( c \in (0, \infty) \). Entonces\[ \E(|(\bs Y \cdot \bs X)_n|) \le \E(|X_0|) + c \sum_{k=1}^n [\E(|X_k|) + \E(|X_{k-1}|)] \lt \infty, \quad n \in \N \] Siguiente, para\( n \in \N \),\ comenzar {alinear*}\ E\ izquierda [(\ bs Y\ cdot\ bs X) _ {n+1}\ mediados\ mathscr {F} _n\ derecha] &=\ E\ izquierda [(\ bs Y\ cdot\ bs X) _n + Y_ {n+1} (X_ {n+1} - x_n)\ mediados\ mathscr {F} _n\ derecha] = (\ bs Y\ cdot\ bs X) _n + Y_ {n+1}\ E\ izquierda (X_ {n+1} - x_n\ mediados\ mathscr {F} _n\ derecha)\\ & = (\ bs Y\ cdot\ bs X ) _n + Y_ {n+1} [\ E (X_ {n+1}\ mid\ mathscr {F} _n) - x_n]\ end {align*} desde\( (\bs Y \cdot \bs X)_n \),\( Y_{n+1} \) y\( X_n \) son\( \mathscr{F}_n \) -medibles. Los resultados se derivan ahora de las definiciones de martingle, sub-martingala y super-martingala.
Esta construcción es conocida como una transformación martingala, y es una versión discreta de la integral estocástica que estudiaremos en el capítulo sobre el movimiento browniano. El resultado también se mantiene si en lugar de\( \bs Y \) estar acotados, hemos\( \bs X \) acotado y\( \E(|Y_n|) \lt \infty \) para\( n \in \N_+ \)
La descomposición de Doob
El siguiente resultado, en tiempo discreto, muestra cómo descomponer un proceso estocástico básico en una martingala y un proceso predecible. El resultado es conocido como el teorema de descomposición de Doob y lleva el nombre de Joseph Doob quien desarrolló gran parte de la teoría moderna de las martingales.
Supongamos que\( \bs X = \{X_n: n \in \N\} \) satisface los supuestos básicos anteriores relativos a la filtración\( \mathfrak F = \{\mathscr{F}_n: n \in \N\} \). Entonces\( X_n = Y_n + Z_n \) para\( n \in \N \) donde\( \bs Y = \{Y_n: n \in \N\} \) es una martingala relativa\( \mathfrak F \) y\( \bs Z = \{Z_n: n \in \N\} \) es predecible relativa a\( \mathfrak F \). La descomposición es única.
- Si\( \bs X \) es una sub-martingala relativa a\( \mathfrak F \) entonces\( \bs Z \) va en aumento.
- Si\( \bs X \) es una super-martingala relativa a\( \mathfrak F \) entonces\( \bs Z \) es decreciente.
Prueba
Recordemos que los supuestos básicos significan que\( \bs X = \{X_n: n \in \N\} \) se adapta a\( \mathfrak F \) y\( \E(|X_n|) \lt \infty \) para\( n \in \N \). Definir\( Z_0 = 0 \) y\[ Z_n = \sum_{k=1}^n \left[\E(X_k \mid \mathscr{F}_{k-1}) - X_{k-1}\right], \quad n \in \N_+ \] Entonces\( Z_n \) es medible con respecto a\( \mathscr{F}_{n-1} \) porque\( n \in \N_+ \) así\( \bs Z \) es predecible con respecto a\( \mathfrak F \). Ahora defina\[ Y_n = X_n - Z_n = X_n - \sum_{k=1}^n \left[\E(X_k \mid \mathscr{F}_{k-1}) - X_{k-1}\right], \quad n \in \N \] Entonces\( \E(|Y_n|) \lt \infty \) y trivialmente\( X_n = Y_n + Z_n \) para\( n \in \N \). Siguiente,\ begin {align*}\ E (Y_ {n+1}\ mid\ mathscr {F} _n) & =\ E (X_ {n+1}\ mid\ mathscr {F} _n) - Z_ {n+1} =\ E (X_ {n+1}\ mid\ mathscr {F} _n) -\ sum_ {k=1} ^ {n+1}\ izquierda [\ E (x_k\ mid\ mathscr {F} _ _ {k-1}) - X_ {k-1}\ derecha]\\ & = x_n -\ sum_ {k=1} ^n\ izquierda [\ E (x_k\ mid\ mathscr {F} _ _ {k-1}) - X_ {k-1}\ derecha] = Y_n,\ quad n\ in\ N\ end {align*} De ahí\( \bs Y \) es una martingala. Por el contrario, supongamos que\( \bs X \) tiene la descomposición en términos de\( \bs Y \) y\( \bs Z \) dada en el teorema. Dado que\( \bs Y \) es una martingala y\( \bs Z \) es predecible,\ begin {align*}\ E (x_n - X_ {n-1}\ mid\ mathscr {F} _ _ {n-1}) & =\ E (Y_n\ mid\ mathscr {F} _ _ {n-1}) -\ E (Y_ {n-1}\ mid\ mathscr {F} _ {n-1}) +\ E (Z_n\ mediados\ mathscr {F} _ {n-1}) -\ E (Z_ {n-1}\ mediados\ mathscr {F} _ _ {n-1})\\ & = Y_ {n-1} - Y_ {n-1} + z_n - Z_ {n-1} = z_n - Z_ {n-1},\ quad n\ in\ N_+\ end {align*} También\( Z_0 = 0 \) así determina de\( \bs X \) manera única\( \bs Z \). Pero\( Y_n = X_n - Z_n \) para\( n \in \N \), tan\( \bs X \) singularmente determina\( \bs Y \) también.
- Si\( \bs X \) es una sub-martingala entonces\( \E(X_n \mid \mathscr{F}_{n-1}) - X_{n-1} \ge 0 \) para\( n \in \N_+ \) eso\( \bs Z \) va en aumento.
- Si\( \bs X \) es una super-martingala entonces\( \E(X_n \mid \mathscr{F}_{n-1}) - X_{n-1} \le 0 \) para\( n \in \N_+ \) así\( \bs Z \) es decreciente.
Una descomposición de esta forma es más complicada en tiempo continuo, en parte porque la definición de un proceso predecible es más sutil y compleja. El teorema de descomposición se mantiene en tiempo continuo, con nuestros supuestos básicos y la suposición adicional de que la colección de variables aleatorias\( \{X_\tau: \tau \text{ is a finite-valued stopping time}\} \) es integrable uniformemente. El resultado es conocido como el teorema de descomposición de Doob-Meyer, nombrado adicionalmente por Paul Meyer.
Procesos de Markov
Como se puede adivinar, existen importantes conexiones entre los procesos de Markov y las martingales. Supongamos que\( \bs X = \{X_t: t \in T\} \) es un proceso de Markov (homogéneo) con espacio estatal\( (S, \mathscr{S}) \), relativo a la filtración\( \mathfrak F = \{\mathscr{F}_t: t \in T\} \). Vamos\( \bs P = \{P_t: t \in T\} \) denotar la colección de kernesl transición de\( \bs X \), de modo que\[ P_t(x, A) = \P(X_t \in A \mid X_0 = x), \quad x \in S, A \in \mathscr{S} \] Recordemos que (como todos los núcleos de probabilidad),\( P_t \) opera (a la derecha) en funciones (medibles)\( h: S \to \R \) por la regla\[ P_t h(x) = \int_S P_t(x, dy) h(y) = \E[h(X_t) \mid X_0 = x], \quad x \in S \] asumiendo como de costumbre que existe el valor esperado. Aquí está la definición crítica que necesitaremos.
Supongamos eso\( h: S \to \R \) y aquello\( \E[|h(X_t)|] \lt \infty \) para\( t \in T \).
- \( h \)es armónico para\( \bs X \) si\( P_t h = h \) para\( t \in T \).
- \( h \)es subarmónico para\( \bs X \) si\( P_t h \ge h \) para\( t \in T \).
- \( h \)es súper armónico para\( \bs X \) si\( P_t h \le h \) para\( t \in T \).
El siguiente teorema da la conexión fundamental entre los dos tipos de procesos estocásticos. Dada la similitud en la terminología, el resultado puede no ser una sorpresa.
Supongamos que\( h: S \to \R \) y\( \E[\left|h(X_t)\right|] \lt \infty \) para\( t \in T \). Definir\( h(\bs X) = \{h(X_t): t \in T\} \).
- \( h \)es armónico para\( \bs X \) si y solo si\( h(\bs X) \) es una martingala con respecto a\( \mathfrak F \).
- \( h \)es subarmónico para\( \bs X \) si y solo si\( h(\bs X) \) es una sub-martingala con respecto a\( \mathfrak F \).
- \( h \)es súper armónico por\( \bs X \) si y solo si\( h(\bs X) \) es una super-martingala con respecto a\( \mathfrak F \).
Prueba
Supongamos que\( s,\, t \in T \) con\( s \le t \). Entonces por la propiedad de Markov,\[ \E[h(X_t) \mid \mathscr{F}_s] = \E[h(X_t) \mid X_s] = P_{t-s} h(X_s) \] Entonces si\( h \) es armónico,\( \E[h(X_t) \mid \mathscr{F}_s] = h(X_s) \) también lo\( \{h(X_t): t \in T\} \) es una martingala. Por el contrario, si\( \{h(X_t): t \in T\} \) es una martingala, entonces\( P_{t-s}h(X_s) = h(X_s) \). Dejar\( s = 0 \) y\( X_0 = x \) dar\( P_t h(x) = h(x) \) así\( h \) es armónico. Las pruebas para sub y super-martingales son similares, con desigualdades que reemplazan las igualdades.
Varios de los ejemplos dados en la Introducción pueden ser reinterpretados en el contexto de las funciones armónicas de las cadenas de Markov. Exploramos algunos de estos a continuación.
Ejemplos
Let\( \mathscr{R} \) denotar el conjunto habitual de subconjuntos mensurables de Borel de\( \R \), y para\( A \in \mathscr{R} \) y\( x \in \R \) let\( A - x = \{y - x: y \in A\} \). Vamos a\( I \) denotar la función de identidad encendido\( \R \), de modo que\( I(x) = x \) para\( x \in \R \). Necesitaremos esta notación en un par de nuestras aplicaciones a continuación.
Paseos Aleatorios
Supongamos que\( \bs V = \{V_n: n \in \N\} \) es una secuencia de variables aleatorias independientes, de valor real, con\( \{V_n: n \in \N_+\} \) idéntica distribución y teniendo común medida de probabilidad\( Q \) sobre\( (\R, \mathscr{R}) \) y media\( a \in \R \). Recordemos de la Introducción que el proceso de suma parcial\( \bs X = \{X_n: n \in \N\} \) asociado con\( \bs V \) está dado por\[ X_n = \sum_{i=0}^n V_i, \quad n \in \N \] y que\( \bs X \) es un paseo aleatorio (discreto-tiempo). Pero también\( \bs X \) es un proceso de Markov en tiempo discreto con kernel de transición de un solo paso\( P \) dado por\( P(x, A) = Q(A - x) \) for\( x \in \R \) y\( A \in \mathscr{R} \).
La función de identidad\( I \) es
- Armónica para\( \bs X \) si\( a = 0 \).
- Subarmónico para\( \bs X \) si\( a \ge 0 \).
- Super-armónico para\( \bs X \) si\( a \le 0 \).
Prueba
Tenga en cuenta que\[ PI(x) = \E(X_1 \mid X_0 = x) = x + \E(X_1 - X_0 \mid X_0 = x) = x + \E(V_1 \mid X_0 = x) = I(x) + a \ \] Desde\( V_1 \) y\( X_0 = V_0 \) son independientes. Los resultados se derivan ahora de las definiciones.
Ahora se deduce de nuestro teorema anterior que\( \bs X \) es una martingala si\( a = 0 \), una sub-martingala si\( a \gt 0 \), y una super-martingala si\( a \lt 0 \). Se mostraron estos resultados directamente a partir de las definiciones de la Introducción.
El simple paseo aleatorio
Supongamos ahora que esa\( \bs{V} = \{V_n: n \in \N\} \) es una secuencia de variables aleatorias independientes con\( \P(V_i = 1) = p \) y\( \P(V_i = -1) = 1 - p \) para\( i \in \N_+ \), donde\( p \in (0, 1) \). Dejar\( \bs{X} = \{X_n: n \in \N\} \) ser el proceso de suma parcial asociado con\( \bs{V} \) lo que\[ X_n = \sum_{i=0}^n V_i, \quad n \in \N \] Entonces\( \bs{X} \) es el simple paseo aleatorio con parámetro\( p \). En cuanto al juego, nuestro jugador juega una secuencia de juegos independientes e idénticos, y en cada juego, gana 1€ con probabilidad\( p \) y pierde 1€ con probabilidad\( 1 - p \). Entonces, si\( X_0 \) es la fortuna inicial del jugador, entonces\( X_n \) es su fortuna neta después de\( n \) los juegos. En la Introducción mostramos que\( \bs X \) es una martingala si\( p = \frac{1}{2} \), una super-martingala si\( p \lt \frac{1}{2} \), y una sub-martingala si\( p \gt \frac{1}{2} \). Pero supongamos ahora que en lugar de hacer apuestas unitarias constantes, el jugador hace apuestas que dependen de los resultados de juegos anteriores. Esto lleva a una transformación martingala como se estudió anteriormente.
Supongamos que el jugador\( Y_n \) apuesta por juego\( n \in \N_+ \) (en apuestas pares), donde\( Y_n \in [0, \infty) \) depende\( (V_0, V_1, V_2, \ldots, V_{n-1}) \) y satisface\( \E(Y_n) \lt \infty \). Por lo que el proceso\( \bs Y = \{Y_n: n \in \N_+\} \) es predecible con respecto a\( \bs X \), y las ganancias netas del jugador después de\( n \) los juegos es\[ (\bs Y \cdot \bs X)_n = V_0 + \sum_{k=1}^n Y_k V_k = X_0 + \sum_{k=1}^n Y_k (X_k - X_{k-1}) \]
- \( \bs Y \cdot \bs X \)es una sub-martingala si\( p \gt \frac{1}{2} \).
- \( \bs Y \cdot \bs X \)es una super-martingala si\( p \lt \frac{1}{2} \).
- \( \bs Y \cdot \bs X \)es una martingala si\( p = \frac{1}{2} \).
Prueba
Estos resultados siguen inmediatamente el teorema para martingala transforma arriba.
La simple caminata aleatoria\( \bs X \) es también una cadena de Markov en tiempo discreto\( \Z \) con una matriz de transición de un solo paso\( P \) dada por\( P(x, x + 1) = p \),\( P(x, x - 1) = 1 - p \).
La función\( h \) dada por\( h(x) = \left(\frac{1 - p}{p}\right)^x \) for\( x \in \Z \) es armónica para\( \bs X \).
Prueba
Para\( x \in \Z \),\ comenzar {alinear*} P h (x) & = p h (x + 1) + (1 - p) h (x - 1) = p\ izquierda (\ frac {1 - p} {p}\ derecha) ^ {x+1} + (1 - p)\ izquierda (\ frac {1 - p} {p}\ derecha) ^ {x-1}\\ &\ frac {1 - p) ^ {x + 1}} {p^x} +\ frac {(1 - p) ^x} {p^ {x-1}} =\ izquierda (\ frac {1 - p} {p}\ derecha) ^x [(1 - p) + p] = h (x)\ final {alinear*}
Ahora se deduce de nuestro teorema anterior que el proceso\( \bs Z = \{Z_n: n \in \N\} \) dado por\( Z_n = \left(\frac{1 - p}{p}\right)^{X_n} \) for\( n \in \N \) es una martingala. Esto lo mostramos directamente desde la definición de la Introducción. Como recordarán, esta es la martingala de De Moivre y lleva el nombre de Abraham De Moivre.
Procesos de ramificación
Recordemos la discusión del proceso de ramificación simple desde la Introducción. La suposición fundamental es que las partículas actúan de manera independiente, cada una con la misma distribución de descendencia\( \N \). Como antes, dejaremos\( f \) denotar la función de densidad de probabilidad (discreta) del número de descendencia de una partícula,\( m \) la media de la distribución y\( \phi \) la función de generación de probabilidad de la distribución. Suponemos que\( f(0) \gt 0 \) y\( f(0) + f(1) \lt 1 \) para que una partícula tenga una probabilidad positiva de morir sin hijos y una probabilidad positiva de producir más de 1 hijo. Recordemos que\( q \) denota la probabilidad de extinción, comenzando con una sola partícula.
El proceso estocástico de interés es\( \bs{X} = \{X_n: n \in \N\} \) donde\( X_n \) está el número de partículas en la generación\( n \) th para\( n \in \N \). Recordemos que\( \bs{X} \) es una cadena de Markov en tiempo discreto\( \N \) con matriz de transición de un solo paso\( P \) dada por\( P(x, y) = f^{* x}(y) \) para\( x, \, y \in \N \) donde\( f^{*x} \) denota el poder de convolución de orden\( x \) de\( f \).
La función\( h \) dada por\( h(x) = q^x \) for\( x \in \N \) es armónica para\( \bs X \).
Prueba
Para\( x \in \N \),\[ Ph(x) = \sum_{y \in \N} P(x, y) h(y) = \sum_{y \in \N} f^{*x}(y) q^y \] La última expresión es la función de generación de probabilidad de\( f^{*x} \) evaluada en\( q \). Pero esta PGF es simple\( \phi^x \) y\( q \) es un punto fijo de\( \phi \) por lo que tenemos\[ Ph(x) = [\phi(q)]^x = q^x = h(x) \]
Ahora se deduce de nuestro teorema anterior que el proceso\( \bs Z = \{Z_n: n \in \N\} \) es una martingala donde\( Z_n = q^{X_n} \) para\( n \in \N \). Esto lo mostramos directamente desde la definición de la Introducción. También demostramos que el proceso\( \bs Y = \{Y_n: n \in \N\} \) es una martingala donde\( Y_n = X_n / m^n \) para\( n \in \N \). Pero no podemos escribir\( Y_n = h(X_n) \) para una función\( h \) definida en el espacio estatal, así que no podemos interpretar esta martingala en términos de una función armónica.
Caminatas aleatorias generales
Supongamos que\( \bs X = \{X_t: t \in T\} \) es un proceso estocástico que satisface los supuestos básicos anteriores relativos a la filtración\( \mathfrak F = \{\mathscr{F}_t: t \in T\} \). Recordemos de la Introducción que el término incremento se refiere a una diferencia de la forma\( X_{s+t} - X_s \) para\( s, \, t \in T \). El proceso\( \bs X \) tiene incrementos independientes si este incremento es siempre independiente de\( \mathscr{F}_s \), y tiene incrementos estacionarios este incremento siempre tiene la misma distribución que\( X_t - X_0 \). En tiempo discreto, un proceso con incrementos estacionarios e independientes es simplemente una caminata aleatoria como se discutió anteriormente. En tiempo continuo, un proceso con incrementos estacionarios e independientes (y con los supuestos de continuidad que hemos impuesto) se llama caminata aleatoria en tiempo continuo, y también un proceso Lévy, llamado así por Paul Lévy.
Entonces supongamos que\( \bs X \) tiene incrementos estacionarios, independientes. Para\( t \in T \) let\( Q_t \) denotar la distribución de probabilidad de\( X_t - X_0 \) on\( (\R, \mathscr{R}) \), así que esa\( Q_t \) es también la distribución de probabilidad aof\( X_{s+t} - X_s \) para cada\( s, \, t \in T \). De nuestro estudio anterior, sabemos que\( \bs X \) es un proceso de Markov con kernel de transición en el\( P_t \) momento\( t \in T \) dado por También\[ P_t(x, A) = Q_t(A - x); \quad x \in \R, A \in \mathscr{R} \] sabemos que\( \E(X_t - X_0) = a t \) para\( t \in T \) dónde\( a = \E(X_1 - X_0) \) (asumiendo por supuesto que el último valor esperado existe en\( \R \)).
La función de identidad\( I \) es.
- Armónica para\( \bs X \) si\( a = 0 \).
- Subarmónico para\( \bs X \) si\( a \ge 0 \).
- Super-armónico para\( \bs X \) si\( a \le 0 \).
Prueba
Tenga en cuenta que\[ P_t I(x) = \E(X_t \mid X_0 = x) = x + \E(X_t - X_0 \mid X_0 = x) = I(x) + a t \] ya que\( X_t - X_0 \) es independiente de\( X_0 \). Los resultados se derivan ahora de las definiciones.
Ahora se deduce que\( \bs X \) es una martingala si\( a = 0 \), una sub-martingala si\( a \ge 0 \), y una super-martingala si\( a \le 0 \). Esto lo mostramos directamente en la Introducción. Recordemos que en tiempo continuo, el proceso de conteo de Poisson tiene incrementos estacionarios e independientes, al igual que el movimiento browniano estándar


