9.1: Clases independientes de variables aleatorias
- Page ID
- 150964
El concepto de independencia para clases de eventos se desarrolla en términos de una regla de producto. En esta unidad, extendemos el concepto a clases de variables aleatorias.
Pares independientes
Recordemos que para una variable aleatoria\(X\), la imagen inversa\(X^{-1} (M)\) (es decir, el conjunto de todos los resultados\(\omega \in \Omega\) que se mapean\(M\) por\(X\)) es un evento para cada subconjunto razonable\(M\) en la línea real. De manera similar, la imagen inversa\(Y^{-1}(N)\) es un evento determinado por variable aleatoria\(Y\) para cada conjunto razonable\(N\). Extendemos la noción de independencia a un par de variables aleatorias requiriendo independencia de los eventos que determinan. Más precisamente,
Definición
Un par\(\{X, Y\}\) de variables aleatorias es (estocásticamente) independiente si cada par de eventos\(\{X^{-1} (M), Y^{-1} (N)\}\) es independiente.
Esta condición puede ser indicada en términos de la regla del producto
\(P(X \in M, Y \le N) = P(X \in M) P(Y \in N)\)para todos (Borel) conjuntos\(M, N\)
Independencia implica
\[ \begin{align*} F_{XY} (t, u) &= P(X \in (-\infty, t], Y \in (-\infty, u]) \\[4pt] &= P(X \in (-\infty, t]) P(Y \in (-\infty, u]) \\[4pt] &= F_X (t) F_Y (u) \quad \forall t, u \end{align*}\]
Tenga en cuenta que la regla de producto en la función de distribución es equivalente a la condición que tiene la regla de producto para las imágenes inversas de una clase especial de conjuntos\(\{M, N\}\) de la forma\(M = (-\infty, t]\) y\(N = (-\infty, u]\). Un teorema importante de la teoría de medidas asegura que si la regla del producto se mantiene para esta clase especial, se mantiene para la clase general de\(\{M, N\}\). Así podemos afirmar
El par\(\{X, Y\}\) es independiente si se mantiene la siguiente regla de producto
\[F_{XY} (t, u) = F_X (t) F_Y (u) \quad \forall t, u\]
Ejemplo 9.1.1: un par independiente
Supongamos\(F_{XY} (t, u) = (1 - e^{-\infty} ) (1 - e^{-\beta u})\)\(0 \le t\),\(0 \le u\). Tomando límites muestra
\[F_X (t) = \lim_{u \to \infty} F_{XY} (t, u) = 1 - e^{-\alpha t} \nonumber\]
y
\[F_Y(u) = \lim_{t \to \infty} F_{XY} (t, u) = 1- e^{-\beta u} \nonumber\]
para que se\(F_{XY} (t, u) = F_X(t) F_Y(u)\) mantenga la regla del producto. Por lo tanto,\(\{X, Y\}\) el par es independiente.
Si hay una función de densidad conjunta, entonces la relación con la función de distribución conjunta deja claro que el par es independiente si la regla del producto se mantiene para la densidad. Es decir, el par es independiente iff
\(f_{XY} (t, u) = f_X (t) f_Y (u)\)\(\forall t, u\)
ejemplo 9.1.2: distribución uniforme conjunta en un rectángulo
supongamos que las distribuciones de masa de probabilidad conjunta inducidas por el par\(\{X, Y\}\) es uniforme en un rectángulo con lados\(I_1 = [a, b]\) y\(I_2 = [c, d]\). Ya que el área es\((b - a) (d - c)\), el valor constante de\(f_{XY}\) es\(1/(b - a) (d - c)\). La integración simple da
\[f_X(t) = \dfrac{1}{(b - a) (d - c)} \int_{c}^{d} du = \dfrac{1}{b - a} \quad a \le t \le b \nonumber\]
y
\[f_Y(u) = \dfrac{1}{(b - a)(d - c)} \int_{a}^{b} dt = \dfrac{1}{d - c} \quad c \le u \le d \nonumber\]
Así se deduce que\(X\) es uniforme en\([a, b]\). \(Y\)es uniforme encendido\([c, d]\), y\(f_{XY} (t, u) = f_X(t) f_Y(u)\) para todos\(t, u\), para que el par\(\{X, Y\}\) sea independiente. Lo contrario también es cierto: si el par es independiente con\(X\) uniforme encendido\([a, b]\) y\(Y\) es uniforme encendido\([c, d]\), el par tiene una distribución conjunta uniforme encendida\(I_1 \times I_2\).
La Distribución Masiva Conjunta
Debe ser evidente que la condición de independencia impone restricciones al carácter de la distribución masiva conjunta en el plano. Para describirlo de manera más sucinta, empleamos la siguiente terminología.
Definición
Si\(M\) es un subconjunto del eje horizontal y\(N\) es un subconjunto del eje vertical, entonces el producto cartesiano\(M \times N\) es el rectángulo (generalizado) que consiste en aquellos puntos\((t, u)\) en el plano tal que\(t \in M\) y\(u \in N\).
ejemplo 9.1.3: Rectángulo con lados de intervalo
El rectángulo en el Ejemplo 9.1.2 es el producto artesiano\(I_1 \times I_2\), que consiste en todos aquellos puntos\((t, u)\) tales que\(a \le t \le b\) y\(c \le u \le d\) (es decir,\(t \in I_1\) y\(u \in I_2\)).
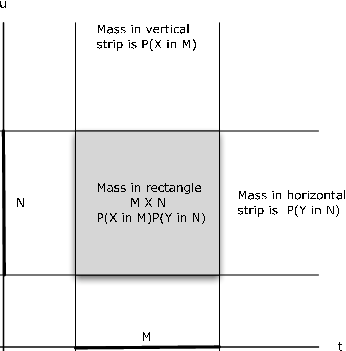
Reafirmamos la regla del producto para la independencia en términos de conjuntos de productos cartesianos.
\[P(X \in M, Y \in N) = P((X, Y) \in M \times N) = P(X \in M) P(Y \in N)\]
La referencia a la Figura 9.1.1 ilustra el patrón básico. Si\(M, N\) hay intervalos en los ejes horizontal y vertical, respectivamente, entonces el rectángulo\(M \times N\) es la intersección de la tira vertical que se encuentra con el eje horizontal\(M\) con la tira horizontal que se encuentra con el eje vertical en\(N\). La probabilidad\(X \in M\) es la porción de la masa de probabilidad conjunta en la franja vertical; la probabilidad\(Y \in N\) es la parte de la probabilidad conjunta en la franja horizontal. La probabilidad en el rectángulo es el producto de estas probabilidades marginales.
Esto sugiere una prueba útil para la no independencia que llamamos prueba de rectángulo. Ilustramos con un ejemplo sencillo.
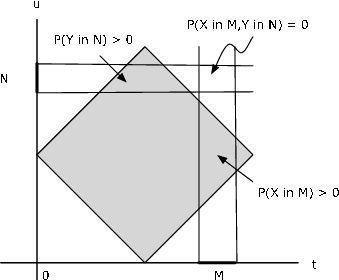
Figura 9.1.2. Prueba de rectángulo para no independencia de un par de variables aleatorias.
Ejemplo 9.1.4: La prueba de rectángulo para la no independencia
Supongamos que la masa de probabilidad se distribuye uniformemente sobre el cuadrado con vértices en (1,0), (2,1), (1,2), (0,1). Es evidente a partir de la Figura 9.1.2 que un valor de\(X\) determina los posibles valores de\(Y\) y viceversa, de manera que no esperaríamos independencia del par. Para establecer esto, considere el pequeño rectángulo que\(M \times N\) se muestra en la figura. No hay masa de probabilidad en la región. Sin embargo\(P(X \in M) > 0\) y\(P(Y \in N) > 0\), para que
\(P(X \in M) P(Y \in N) > 0\), pero\(P((X, Y) \in M \times N) = 0\). La regla del producto falla; de ahí que el par no pueda ser estocásticamente independiente.
Obración. Hay casos no independientes para los que esta prueba no funciona. Y no proporciona una prueba de independencia. A pesar de estas limitaciones, frecuentemente es útil. Debido a la información contenida en la condición de independencia, en muchos casos se pueden obtener las distribuciones completas conjuntas y marginales con información parcial apropiada. El siguiente es un ejemplo sencillo.
Ejemplo 9.1.5: Probabilidades conjuntas y marginales a partir de información parcial
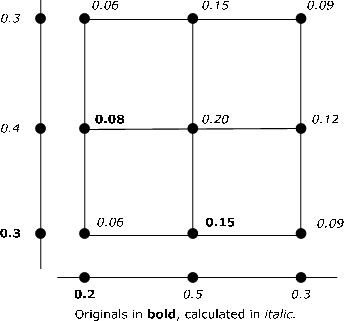
Supongamos que el par\(\{X, Y\}\) es independiente y cada uno tiene tres valores posibles. Los siguientes cuatro elementos de información están disponibles.
\(P(X = t_1) = 0.2\),\(P(Y = u_1) = 0.3\),\(P(X = t_1, Y = u_2) = 0.08\)
\(P(X = t_2, Y = u_1) = 0.15\)
Estos valores se muestran en negrita en la Figura 9.1.3. Se utiliza una combinación de la regla del producto y el hecho de que la masa de probabilidad total es uno para calcular cada una de las probabilidades marginales y conjuntas. Por ejemplo\(P(X = t_1) = 0.2\) e\(P(X = t_1, Y = u_2) = P(X = t_1) P(Y = u_2) = 0.8\) implica\(P(Y = u_2) = 0.4\). Entonces P (Y = u_3) = 1 - P (Y = u_1) - P (Y = u_2) = 0.3\). Otros se calculan de manera similar. No existe un procedimiento único para la solución. Y no ha parecido útil desarrollar procedimientos de MATLAB para lograrlo.
Ejemplo 9.1.6: La distribución normal conjunta
Un par\(\{X, Y\}\) tiene la distribución normal de la junta si la densidad de la junta es
\(f_{XY} (t, u) = \dfrac{1}{2\pi \sigma_{X} \sigma_{Y} (1 - \rho^2)^{1/2}} e^{-Q(t,u)/2}\)
donde
\(Q(t, u) = \dfrac{1}{1 - \rho^2} [(\dfrac{t - \mu_X}{\sigma_X})^2 - 2 \rho (\dfrac{t - \mu_X}{\sigma_X}) (\dfrac{t - \mu_Y}{\sigma_Y}) + (\dfrac{t - \mu_Y}{\sigma_Y})^2]\)
Las densidades marginales se obtienen con la ayuda de algunos trucos algebraicos para integrar la densidad articular. El resultado es que\(X ~ N(\mu_X, \sigma_X^2)\) y\(Y ~ N(\mu_Y, \sigma_Y^2)\). Si el parámetro\(\rho\) se establece en cero, el resultado es
\(f_{XY} (t, u) = f_X (t) f_Y(u)\)
para que el par sea independiente iff\(\rho = 0\). Los detalles se dejan como ejercicio para el lector interesado.
Obración. Si bien es cierto que cada par independiente de variables aleatorias normalmente distribuidas es normal conjunta, no todos los pares de variables aleatorias normalmente distribuidas tienen la distribución normal conjunta.
Ejemplo 9.1.7: un par normal no articular normalmente distribuido
Comenzamos con la distribución para un par normal de articulación y derivamos una distribución conjunta para un par normal que no es normal de articulación. La función
\(\varphi (t, u) = \dfrac{1}{2\pi} \text{exp } (-\dfrac{t^2}{2} - \dfrac{u^2}{2})\)
es la densidad normal conjunta para un par independiente (\(\rho = 0\)) de variables aleatorias normales estandarizadas. Ahora defina la densidad de juntas para un par\(\{X, Y\}\) por
\(f_{XY} (t, u) = 2 \varphi (t, u)\)en los cuadrantes primero y tercero, y cero en otros
Tanto\(X\) ~\(N(0,1)\) como\(Y\) ~\(N(0,1)\). Sin embargo, no pueden ser normales en las articulaciones, ya que la distribución normal de la articulación es positiva para all (\(t, u\)).
Clases independientes
Dado que la independencia de las variables aleatorias es la independencia de los eventos determinados por las variables aleatorias, la extensión a clases generales es simple e inmediata.
Definición
Una clase\(\{X_i: i \in J\}\) de variables aleatorias es (estocásticamente) independiente si la regla del producto tiene para cada subclase finita de dos o más.
Obración. El conjunto de índices\(J\) en la definición puede ser finito o infinito.
Para una clase finita\(\{X_i: 1 \le i \le n\}\), la independencia es equivalente a la regla del producto
\(F_{X_1 X_2 \cdot\cdot\cdot X_n} (t_1, t_2, \cdot\cdot\cdot, t_n) = \prod_{i = 1}^{n} F_{X_i} (t_i)\)para todos\((t_1, t_2, \cdot\cdot\cdot, t_n)\)
Dado que podemos obtener la función de distribución conjunta para cualquier subclase finita dejando que los argumentos para las otras sean ∞ (es decir, tomando los límites como el\(t_i\) aumento apropiado sin límite), la regla de producto único es suficiente para dar cuenta de todas las subclases finitas.
Variables aleatorias absolutamente continuas
Si una clase\(\{X_i: i \in J\}\) es independiente y las variables individuales son absolutamente continuas (es decir, tienen densidades), entonces cualquier subclase finita es conjuntamente absolutamente continua y la regla de producto se mantiene para las densidades de tales subclases
\(f_{X_{i1}X_{i2} \cdot\cdot\cdot X_{im}} (t_{i1}, t_{i2}, \cdot\cdot\cdot, t_{im}) = \prod_{k = 1}^{m} f_{X_{ik}} (t_{ik})\)para todos\((t_1, t_2, \cdot\cdot\cdot, t_n)\)
Del mismo modo, si cada subclase finita es conjuntamente absolutamente continua, entonces cada variable individual es absolutamente continua y la regla del producto se mantiene para las densidades. Frecuentemente tratamos con clases independientes en las que cada variable aleatoria tiene la misma distribución marginal. Dichas clases se denominan clases iid (un acrónimo de i ndependiente, i denticamente d istributed). Los ejemplos son muestras aleatorias simples de una población determinada, o los resultados de ensayos repetitivos con la misma distribución sobre el resultado de cada ensayo componente. Una secuencia de Bernoulli es un ejemplo sencillo.
Variables aleatorias simples
Considere un par\(\{X, Y\}\) de variables aleatorias simples en forma canónica
\(X = \sum_{i = 1}^{n}t_i I_{A_i}\)\(Y = \sum_{j = 1}^{m} u_j I_{B_j}\)
Dado que\(A_i = \{X = t_i\}\) y\(B_j = \{Y = u_j\}\) el par\(\{X, Y\}\) es independiente si cada uno de los pares\(\{A_i, B_j\}\) es independiente. La distribución conjunta tiene masa de probabilidad en cada punto\((t_i, u_j)\) en el rango de\(W = (X, Y)\). Por lo tanto, en cada punto de la cuadrícula,
\(P(X = t_i, Y = u_j) = P(X = t_i) P(Y = u_j)\)
De acuerdo con la prueba de rectángulo, ningún punto de cuadrícula que tenga uno de los\(t_i\) o\(u_j\) como coordenada tiene masa de probabilidad cero. Las distribuciones marginales determinan las distribuciones conjuntas. Si\(X\) tiene valores\(n\) distintos y\(Y\) tiene valores\(m\) distintos, entonces las probabilidades marginales n + m son suficientes para determinar las probabilidades conjuntas m · n. Dado que las probabilidades marginales para cada variable deben sumar a una, solo se necesitan\(n - 1) + (m - 1) = m + n - 2\) valores.
Supongamos\(X\) y\(Y\) están en forma afín. Es decir,
\(X =a_0 + \sum_{i = 1}^{n} a_i I_{E_i}\)\(Y = b_0 + \sum_{j = 1}^{m} b_j I_{E_j}\)
Dado que\(A_r = \{X = t_r\}\) es la unión de minterms generada por el\(E_i\) y\(B_j = \{Y = u_s\}\) es la unión de minterms generados por el\(F_j\), el par\(\{X, Y\}\) es independiente si cada par de minterms\(\{M_a, N_b\}\) generados por las dos clases, respectivamente, es independiente. La independencia de los pares minterm está implicada por la independencia de la clase combinada
\(\{E_i, F_j: 1 \le i \le n, 1 \le j \le m\}\)
Los cálculos en el caso simple conjunto se manejan fácilmente mediante funciones m y procedimientos m apropiados.
MATLAB y variables aleatorias simples independientes
En el caso general de pares de variables aleatorias simples conjuntas tenemos el procedimiento m jcalc, que utiliza información en matrices\(X, Y\) y\(P\) para determinar las probabilidades marginales y las matrices de cálculo\(t\) y\(u\). En el caso independiente, solo necesitamos las distribuciones marginales en matrices\(X\),\(PX\),\(Y\) y\(PY\) para determinar la matriz de probabilidad conjunta (de ahí la distribución conjunta) y las matrices de cálculo\(t\) y\(u\). Si las variables aleatorias se dan en forma canónica, tenemos las distribuciones marginales. Si están en forma afín, podemos usar canónicos (o la forma de función canonicf) para obtener las distribuciones marginales.
Una vez que tenemos ambas distribuciones marginales, utilizamos un procedimiento m que llamamos icalc. La formación de la matriz de probabilidad conjunta es simplemente una cuestión de determinar todas las probabilidades conjuntas
\(p(i, j) = P(X = t_i, Y = u_j) = P(X = t_i) P(Y = u_j)\)
Una vez calculados estos, la formación de las matrices de cálculo\(t\) y\(u\) se logra exactamente como en jcalc.
Ejemplo 9.1.8: Uso de icalc para configurar cálculos conjuntos
X = [-4 -2 0 1 3];
Y = [0 1 2 4];
PX = 0.01*[12 18 27 19 24];
PY = 0.01*[15 43 31 11];
icalc
Enter row matrix of X-values X
Enter row matrix of Y-values Y
Enter X probabilities PX
Enter Y probabilities PY
Use array operations on matrices X, Y, PX, PY, t, u, and P
disp(P) % Optional display of the joint matrix
0.0132 0.0198 0.0297 0.0209 0.0264
0.0372 0.0558 0.0837 0.0589 0.0744
0.0516 0.0774 0.1161 0.0817 0.1032
0.0180 0.0270 0.0405 0.0285 0.0360
disp(t) % Calculation matrix t
-4 -2 0 1 3
-4 -2 0 1 3
-4 -2 0 1 3
-4 -2 0 1 3
disp(u) % Calculation matrix u
4 4 4 4 4
2 2 2 2 2
1 1 1 1 1
0 0 0 0 0
M = (t>=-3)&(t<=2); % M = [-3, 2]
PM = total(M.*P) % P(X in M)
PM = 0.6400
N = (u>0)&(u.^2<=15); % N = {u: u > 0, u^2 <= 15}
PN = total(N.*P) % P(Y in N)
PN = 0.7400
Q = M&N; % Rectangle MxN
PQ = total(Q.*P) % P((X,Y) in MxN)
PQ = 0.4736
p = PM*PN
p = 0.4736 % P((X,Y) in MxN) = P(X in M)P(Y in N)
Como ejemplo, considere nuevamente el problema de los ensayos conjuntos de Bernoulli descritos en el tratamiento de 4.3 Ensayos compuestos.
Ejemplo 9.1.9: El ensayo conjunto de Bernoulli del Ejemplo 4.9
1 Bill y Mary se llevan diez tiros libres de basquetbol cada uno. Suponemos que las dos secuencias de ensayos son independientes entre sí, y cada una es una secuencia de Bernoulli.
María: Tiene probabilidad de 0.80 de éxito en cada ensayo.
Bill: Tiene probabilidad 0.85 de éxito en cada juicio.
¿Cuál es la probabilidad de que Mary realice más tiros libres que Bill?
Solución
\(X\)Sea el número de goles que hace Mary y\(Y\) sea el número que haga Bill. Entonces\(X\) ~ binomio (10, 0.8) y\(Y\) ~ binomio (10, 0.85).
X = 0:10; Y = 0:10; PX = ibinom(10,0.8,X); PY = ibinom(10,0.85,Y); icalc Enter row matrix of X-values X % Could enter 0:10 Enter row matrix of Y-values Y % Could enter 0:10 Enter X probabilities PX % Could enter ibinom(10,0.8,X) Enter Y probabilities PY % Could enter ibinom(10,0.85,Y) Use array operations on matrices X, Y, PX, PY, t, u, and P PM = total((t>u).*P) PM = 0.2738 % Agrees with solution in Example 9 from "Composite Trials". Pe = total((u==t).*P) % Additional information is more easily Pe = 0.2276 % obtained than in the event formulation Pm = total((t>=u).*P) % of Example 9 from "Composite Trials". Pm = 0.5014
Ejemplo 9.1.10: Pruebas contrarreloj Sprinters
Doce velocistas de clase mundial en un encuentro corren en dos series de seis personas cada una. Cada corredor tiene una probabilidad razonable de romper el récord de la pista. Suponemos que los resultados para los individuos son independientes.
Probabilidades de primer calor: 0.61 0.73 0.55 0.81 0.66 0.43
Probabilidades de segundo calor: 0.75 0.48 0.62 0.58 0.77 0.51
Compara las dos series para números que rompen el récord de la pista.
Solución
\(X\)Sea el número de éxitos en la primera serie y\(Y\) sea el número que tenga éxito en la segunda serie. Entonces el par\(\{X, Y\}\) es independiente. Utilizamos la función m canonicf para determinar las distribuciones para\(X\) y para\(Y\), luego icalc para obtener la distribución conjunta.
c1 = [ones(1,6) 0]; c2 = [ones(1,6) 0]; P1 = [0.61 0.73 0.55 0.81 0.66 0.43]; P2 = [0.75 0.48 0.62 0.58 0.77 0.51]; [X,PX] = canonicf(c1,minprob(P1)); [Y,PY] = canonicf(c2,minprob(P2)); icalc Enter row matrix of X-values X Enter row matrix of Y-values Y Enter X probabilities PX Enter Y probabilities PY Use array operations on matrices X, Y, PX, PY, t, u, and P Pm1 = total((t>u).*P) % Prob first heat has most Pm1 = 0.3986 Pm2 = total((u>t).*P) % Prob second heat has most Pm2 = 0.3606 Peq = total((t==u).*P) % Prob both have the same Peq = 0.2408 Px3 = (X>=3)*PX' % Prob first has 3 or more Px3 = 0.8708 Py3 = (Y>=3)*PY' % Prob second has 3 or more Py3 = 0.8525
Como en el caso de jcalc, tenemos una versión m-function icalcf
[x, y, t, u, px, py, p] = icalcf (X, Y, PX, PY)\)
Tenemos una función m relacionada idbn para obtener la matriz de probabilidad conjunta a partir de las probabilidades marginales. Su formación de la matriz conjunta utiliza las mismas operaciones que icalc.
Ejemplo 9.1.11: Un ejemplo numérico
PX = 0.1*[3 5 2];
PY = 0.01*[20 15 40 25];
P = idbn(PX,PY)
P =
0.0750 0.1250 0.0500
0.1200 0.2000 0.0800
0.0450 0.0750 0.0300
0.0600 0.1000 0.0400
Un m- procedimiento itest verifica una distribución conjunta para la independencia. Esto lo hace calculando los marginales, formando luego una matriz de prueba conjunta independiente, la cual se compara con la original. Normalmente no se exhibe la matriz\(P\) a ensayar. No obstante, este es un caso en el que la regla del producto se mantiene para la mayoría de los minterms, y sería muy difícil escoger aquellos para los que falla. El procedimiento m simplemente verifica todos ellos.
idemo1 % Joint matrix in datafile idemo1
P = 0.0091 0.0147 0.0035 0.0049 0.0105 0.0161 0.0112
0.0117 0.0189 0.0045 0.0063 0.0135 0.0207 0.0144
0.0104 0.0168 0.0040 0.0056 0.0120 0.0184 0.0128
0.0169 0.0273 0.0065 0.0091 0.0095 0.0299 0.0208
0.0052 0.0084 0.0020 0.0028 0.0060 0.0092 0.0064
0.0169 0.0273 0.0065 0.0091 0.0195 0.0299 0.0208
0.0104 0.0168 0.0040 0.0056 0.0120 0.0184 0.0128
0.0078 0.0126 0.0030 0.0042 0.0190 0.0138 0.0096
0.0117 0.0189 0.0045 0.0063 0.0135 0.0207 0.0144
0.0091 0.0147 0.0035 0.0049 0.0105 0.0161 0.0112
0.0065 0.0105 0.0025 0.0035 0.0075 0.0115 0.0080
0.0143 0.0231 0.0055 0.0077 0.0165 0.0253 0.0176
itest
Enter matrix of joint probabilities P
The pair {X,Y} is NOT independent % Result of test
To see where the product rule fails, call for D
disp(D) % Optional call for D
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
1 1 1 1 1 1 1
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
1 1 1 1 1 1 1
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
A continuación, consideramos un ejemplo en el que se sabe que la pareja es independiente.
jdemo3 % call for data in m-file
disp(P) % call to display P
0.0132 0.0198 0.0297 0.0209 0.0264
0.0372 0.0558 0.0837 0.0589 0.0744
0.0516 0.0774 0.1161 0.0817 0.1032
0.0180 0.0270 0.0405 0.0285 0.0360
itest
Enter matrix of joint probabilities P
The pair {X,Y} is independent % Result of test
El procedimiento icalc se puede extender para tratar con una clase independiente de tres variables aleatorias. Llamamos al procedimiento m icalc3. El siguiente es un ejemplo sencillo de su uso.
Ejemplo 9.1.14: Cálculos para tres variables aleatorias independientes
X = 0:4; Y = 1:2:7; Z = 0:3:12; PX = 0.1*[1 3 2 3 1]; PY = 0.1*[2 2 3 3]; PZ = 0.1*[2 2 1 3 2]; icalc3 Enter row matrix of X-values X Enter row matrix of Y-values Y Enter row matrix of Z-values Z Enter X probabilities PX Enter Y probabilities PY Enter Z probabilities PZ Use array operations on matrices X, Y, Z, PX, PY, PZ, t, u, v, and P G = 3*t + 2*u - 4*v; % W = 3X + 2Y -4Z [W,PW] = csort(G,P); % Distribution for W PG = total((G>0).*P) % P(g(X,Y,Z) > 0) PG = 0.3370 Pg = (W>0)*PW' % P(Z > 0) Pg = 0.3370
También está disponible un procedimiento m icalc4 para manejar una clase independiente de cuatro variables. También se utilizan varias variaciones de la función m mgsum y la función m diidsum para obtener distribuciones para sumas de variables aleatorias independientes. Los consideramos en diversos contextos en otras unidades.
Aproximación para el caso absolutamente continuo
En el estudio de funciones de variables aleatorias, mostramos que una variable aleatoria simple aproximada\(X_s\) del tipo que usamos es una función de la variable aleatoria\(X\) que se aproxima. Además, demostramos que si\(\{X, Y\}\) es un par independiente, también lo es\(\{g(X), h(Y)\}\) para cualquier función razonable\(g\) y\(h\). Así si\(\{X, Y\}\) es un par independiente, también lo es cualquier par de aproximar funciones simples\(\{X_s, Y_s\}\) del tipo considerado. Ahora es teóricamente posible que el par aproximado\(\{X_s, Y_s\}\) sea independiente, pero que el par aproximado\(\{X, Y\}\) no sea independiente. Pero esto es muy poco probable. Para todos los fines prácticos, podemos\(\{X, Y\}\) considerar independientes si\(\{X_s, Y_s\}\) es independiente. En caso de duda, considere un segundo par de funciones simples aproximadas con más puntos de subdivisión. Esto disminuye aún más la probabilidad de una falsa indicación de independencia por las variables aleatorias aproximadas.
Ejemplo 9.1.15: Un par independiente
Supongamos\(X\) ~ exponencial (3) y\(Y\) ~ exponencial (2) con
\(f_{XY} (t, u) = 6e^{-3t} e^{-2u} = 6e^{-(3t+2u)}\)\(t \ge 0, u \ge 0\)
Ya que\(e^{-12} \approx 6 \times 10^{-6}\), aproximamos\(X\) para valores hasta 4 y\(Y\) para valores hasta 6.
tuappr
Enter matrix [a b] of X-range endpoints [0 4]
Enter matrix [c d] of Y-range endpoints [0 6]
Enter number of X approximation points 200
Enter number of Y approximation points 300
Enter expression for joint density 6*exp(-(3*t + 2*u))
Use array operations on X, Y, PX, PY, t, u, and P
itest
Enter matrix of joint probabilities P
The pair {X,Y} is independent
Ejemplo 9.1.16: Prueba de independencia
El par\(\{X, Y\}\) tiene densidad de juntas\(f_{XY} (t, u) = 4tu\)\(0 \le t \le 1\),\(0 \le u \le 1\). Es bastante fácil determinar los marginales en este caso. Por simetría, son lo mismo.
\(f_X(t) = 4t \int_{0}^{1} udu = 2t\),\(0 \le t \le 1\)
de manera\(f_{XY} = f_X f_Y\) que lo que asegura que el par sea independiente. Considera la solución usando tuappr e itest.
tuappr
Enter matrix [a b] of X-range endpoints [0 1]
Enter matrix [c d] of Y-range endpoints [0 1]
Enter number of X approximation points 100
Enter number of Y approximation points 100
Enter expression for joint density 4*t.*u
Use array operations on X, Y, PX, PY, t, u, and P
itest
Enter matrix of joint probabilities P
The pair {X,Y} is independent


