4.5.3: Índice de refracción
- Page ID
- 51129
Estamos llegando a nuestro objetivo declarado de expresar el índice de refracción en función de los parámetros microscópicos del material. Como \(n_{c}^{2}=(n+i \kappa)^{2}=\epsilon_{g e n} / \epsilon_{0}\)
\[
n_{c}^{2}=1+N_{V} \frac{q^{2}}{m \epsilon_{0}} \sum_{j} \frac{f_{j}}{\omega_{0 j}^{2}-\omega^{2}-i \gamma_{j} \omega}-N_{V}^{\prime} \frac{q^{2}}{m \epsilon_{0}} \frac{1}{\omega(\omega+i \gamma)} \notag
\]
nuestro siguiente objetivo es despejar de ahí \(n\) y \(\kappa\). Pero ya podemos decir dos cosas
- en general, los medios van a ser dispersivos: en este índice de refracción hay una marcada dependencia de la fercuencia en casi todos los términos.
- podemos decir lo mismo respecto al carácter complejo: en general habrá una parte compleja del índice de refracción. Lo absorbente que sea el medio dependerá de la frecuencia, pero en general en alguna parte del espectro el medio será absorbente.
- esta fórmula también contempla la posibilidad de medios inhomogéneos, a través de una dependencia espacial de las densidades de cargas libres y ligadas, \(N_{V}^{\prime}\) y \(N_{V}\).
Ya estamos listos para demostrar la afirmación que hicimos de que
\[
\Im\left\{\epsilon_{g e n}\right\} \propto \gamma_{j}, \gamma>0 \notag
\]
esto se deduce multiplicando y dividiendo por los complejos conjugados de los denominadores en los dos últimos términos. Como ambos parámetros \(\gamma_{j}, \gamma\) describen pérdidas, son constantes positivas por definición, por lo que se encuentra la relación expuesta y, consecuentemente \(\mathbf{k} \cdot \mathbf{a} \geq 0\). Proseguiremos tratando de separar parte imaginaria y real del índice de refracción, y para ello abordaremos dos casos simples
Dieléctrico: no hay cargas libres
Para un dieléctrico sólo tenemos la primera contribución:
\[
n_{c}^{2}=1+N_{V} \frac{q^{2}}{m \epsilon_{0}} \sum_{j} \frac{f_{j}}{\omega_{0 j}^{2}-\omega^{2}-i \gamma_{j} \omega} \notag
\]
Esta expresión proviene de aproximar el campo eléctrico macroscópico por un sumatorio, lo que sólo se podía hacer si \(\frac{N_{V} \alpha}{\epsilon_{0}} \ll 1\) (normalmente gases diluídos). Podemos aprovechar este dato y utilizar la aproximación lineal de la raíz cuadrada
\[
\sqrt{1+x} \approx 1+\frac{x}{2} \notag
\]
Después extraemos parte real e imaginaria
\[
\begin{aligned}
n+i \kappa &=1+N_{V} \frac{q^{2}}{2 m \epsilon_{0}} \sum_{j} \frac{f_{j}}{\omega_{0 j}^{2}-\omega^{2}-i \gamma_{j} \omega} \\
n &=1+N_{V} \frac{q^{2}}{2 m \epsilon_{0}} \sum_{j} \frac{\left(\omega_{0, j}^{2}-\omega^{2}\right) f_{j}}{\left(\omega_{0 j}^{2}-\omega^{2}\right)^{2}+\gamma_{j}^{2} \omega} \\
\kappa &=N_{V} \frac{q^{2}}{2 m \epsilon_{0}} \sum_{j} \frac{\omega \gamma_{j} f_{j}}{\left(\omega_{0, j}^{2}-\omega^{2}\right)^{2}+\gamma_{j}^{2} \omega^{2}}
\end{aligned}
\]
La parte imaginaria vale 0 a no ser que estemos en las proximidades de las resonancias, zonas denominadas bandas de absorción. La anchura de estos picos de \(\kappa\) es proporcional a \(\gamma_{j}\). Una primera conclusión importante es que no existen medios transparentes o absorbentes en todo el espectro electromagnético. Los vidrios de ventana por ejemplo son muy opacos al ultravioleta.
Para átomos aislados (sin interacciones con el entorno) los picos se parecen a deltas de DiraC. Si empezamos a considerar medios más densos (gases a presión creciente) la anchura de las bandas crece. Las bandas pueden estar próximas, y si es así, se superponen
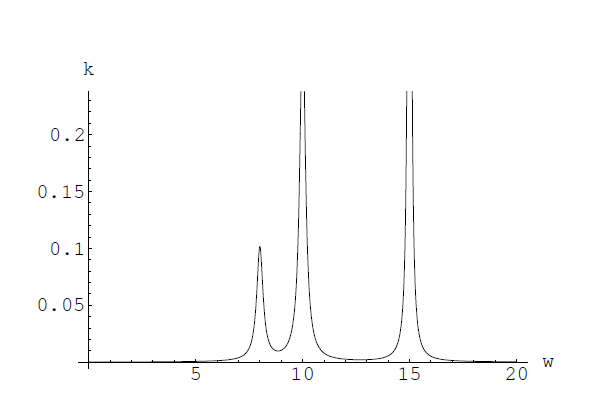

muchos picos para dar lugar a una verdadera banda ancha que puede cubrir todo el visible, como ocurre con los metales. En general, las bandas de absorción de una mezcla de gases son la superposición de las bandas de absorción individuales (figura \(\PageIndex{2}\)).
Como vemos, se puede obtener información sobre la materia estudiando cómo se propaga la luz en ella. El análisis espectral de una substancia nos indica sus frecuencias de resonancia, y la anchura de las líneas de absorción nos da información sobre los paráme\(\operatorname{tros} \gamma\). Las zonas donde \(\kappa\) vale cero son de transmisión perfecta, sin absorción.
De estos gráficos sólo se pide un conocimiento cualitativo.
Podemos representar también la parte real, \(n(\omega)\) (figura \(\PageIndex{3}\)). Se trata de una cantidad creciente \(\left(\frac{\mathrm{d} n}{\mathrm{~d} \omega}>0\right)\) para las zonas de transparencia, y cómo una buena condición para identificar las zonas de absorción es justo la contraria, \(\left(\frac{\mathrm{d} n}{\mathrm{~d} \omega}<0\right)\). Las zonas así caracterizadas reciben la denominación, respectivamente, de zona de dispersión normal y zona de dispersión anómala 4 .
La dispersión normal se da en transparencia y es fácilmente observable, mientras que la dispersión anómala recibe ese nombre porque es raramente observable, ya que se encuentra en la zona de absorción.

Conductor: hay cargas libres
Las cargas libres contribuyen al índice de refracción complejo del siguiente modo:
\[
n_{c}^{2}=1-N_{V}^{\prime} \frac{q^{2}}{m \epsilon_{0}} \frac{1}{\omega(\omega+\gamma)} \notag
\]
Suponemos que sólo hay cargas libres aunque generalmente también hay cargas ligadas. Algunos valores para el caso particular del cobre son
\[
\begin{aligned}
N_{V}^{\prime} &=8 \times 10^{28} \frac{e^{-}}{m^{3}} \\
\gamma &=4 \times 10^{13} s^{-1}
\end{aligned}
\]
Aunque \(\gamma\) es mayor que antes, todavía se cumple que \(\gamma \ll \omega\) y por eso podemos hacer la siguiente aproximación
\[
\begin{aligned}
n_{c}^{2} & \approx 1-N_{V}^{\prime} \frac{q^{2}}{m \epsilon_{0}} \frac{1}{\omega^{2}} \\
& \approx 1-\frac{\omega_{p}^{2}}{\omega^{2}}
\end{aligned}
\]
donde se define la frecuencia de plasma
\[
\omega_{p} \equiv \sqrt{N_{V}^{\prime} \frac{q^{2}}{m \epsilon_{0}}} \notag
\]
para el cobre la frecuencia de plasma es \(\omega_{p}=1.6 \times 10^{16} \frac{\mathrm{rad}}{\mathrm{s}}\) y corresponde al ultravioleta.
Vamos a estudiar dos casos
1. Visible \(\omega<\omega_{p}\) implica que \(n_{c}^{2}<0\) con lo cual \(n_{c}=i \kappa\) (hay una parte real, pero ha desaparecido por la doble aproximación que hemos hecho).
\[
\kappa=\sqrt{\frac{\omega_{p}}{\omega^{2}}-1} \notag
\]
Para el cobre en el visible \(\omega \approx 3 \times 10^{15} \mathrm{rad} / \mathrm{s}\), de modo que \(\kappa \approx 5\). El cálculo no es muy exacto, pero da bien el orden del índice de refracción. El valor de \(\kappa\) es bastante grande, en consonancia con el hecho de que los metales son opacos a la radiación visible.
2. \(\omega>\omega_{p}\) de modo que \(n_{c}^{2}>0 ;\) es decir \(n_{c}=n\). El coeficiente de absorción es nulo. Lo que en el visible era fuertemente absorbente en el UV \(\left(\omega_{p}<\omega\right)\) pasa a ser transparente y viceversa.
___________________________________________________________________________
1. en dispersión anómala la velocidad de fase es mayor que \(c\), el índice de refracción es \(<1\) y las longitudes de onda cortas se refractan menos que las largas. Ver [Born].

