9.5.2: Tratamiento cuantitativo de la distribución de intensidad
- Page ID
- 51193
Si estamos interesados en interferencia estamos interesados en maximizar la visibilidad. Según la expresión hallada, \(V \rightarrow 1\) cuando \(F \gg 1\). \(F\) depende de los coeficientes de reflexión de las láminas metálicas. La condición que hemos exigido es equivalente a
\[
\left|r_{1} r_{2}\right| \rightarrow 1 \notag
\]
Este interferómetro se diferencia de los otros en que la onda producida es suma de un número infinito de ondas. Los interferómetros de YOUNG y MiCHELSON daban lugar a una distribución de intensidad de la forma
\[
I=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \varphi \notag
\]
La interferencia depende mediante un coseno de la diferencia de fases. Esto es así siempre que se hacen interferir dos ondas. Sin embargo, aquí la dependencia de la intensidad de la diferencia de fase es completamente diferente
\[
I^{\prime}=\frac{T_{\max }}{1+F \sin ^{2} \varphi} I \notag
\]
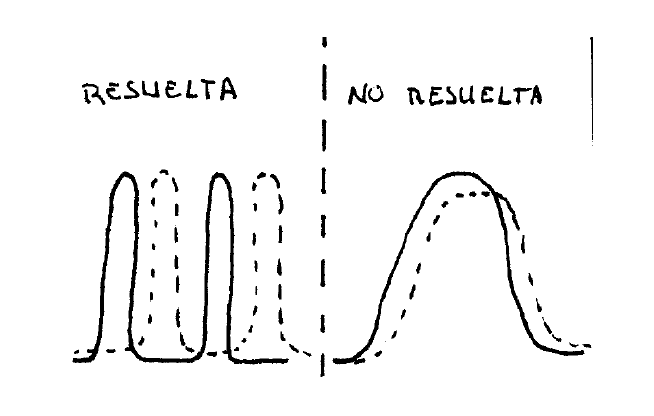
El interés de este interferómetro consiste en explotar su singularidad, que se expresa en la figura \(\mathcal{T}(\varphi)\). Una forma de caracterizar esta distribución de intensidades es cuantificar la anchura de los picos. Esto se puede hacer, por ejemplo, identificando cuál es la anchura \(\delta \varphi\) a mitad de altura, es decir, a \(\frac{\mathcal{T}_{\max }}{2}\). Observemos que
\[
\begin{aligned}
\mathcal{T}\left(m \pi+\frac{\delta \varphi}{2}\right) &=\frac{\mathcal{I}_{\max }}{2} \\
\frac{1}{1+F \sin ^{2}\left(\frac{\delta \varphi}{2}\right)} &=\frac{1}{2} \\
\sin \left(\frac{\delta \varphi}{2}\right) &=\frac{1}{\sqrt{F}}
\end{aligned}
\]
por lo que
\[
\delta \varphi=2 \arcsin \left(\frac{1}{\sqrt{F}}\right) \notag
\]
Como estamos interesados en \(F \gg 1\), podemos hacer un desarrollo en serie de potencias
\[
\delta \varphi \simeq \frac{2}{\sqrt{F}} \notag
\]
Cuanto mejor sea la visibilidad ( \(F\) más alto) tanto más estrechos serán los picos.
Estudiar un interferómetro de FP construído con dos láminas metálicas de plata.
Solution
Para la plata, \(\left|r_{1} r_{2}\right| \simeq 0.94\). Con esto, \(F \simeq 10^{3}\). La visibilidad es buena, \(V=0.998\). La anchura a mitad de altura es \(\delta \varphi \simeq 0.06\). Como la plata es un medio absorbente, la transmitancia en el máximo no será la unidad; una parte será absorbida: \(T_{\max }=0.44\) (en el máximo tenemos la mitad de la intensidad incidente). Hay que subrayar que \(\delta \varphi\) es muy pequeño, ya que es, relativo a la separación entre picos, \(\frac{0.06}{3.14} \simeq 2 \%\). Esta figura interferencial y la producida por dos ondas son muy distintas.

