10.6.1: Abertura rectangular
- Page ID
- 51206
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
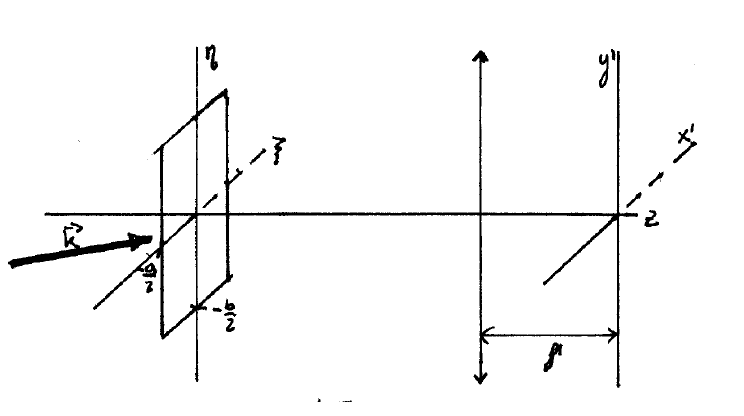
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La función de transmisión en el plano de las aberturas es \(t(\xi, \eta)=1\) si \(\xi, \eta \in \Sigma\) y \(t(\xi, \eta)=0\) para fuera de la rendija. La iluminación es una oap
\[
u=u_{0} e^{i \mathbf{k} \cdot \mathbf{r}} u(\xi, \eta)=u_{0} e^{i\left(k_{x} \xi+k_{y} \eta\right)} \notag
\]
Sólo queda hacer la integral
\[
\begin{aligned}
\hat{u}\left(x^{\prime}, y^{\prime}\right) & \propto \int_{-\frac{a}{2}}^{\frac{a}{2}} d \xi \int_{-\frac{b}{2}}^{\frac{b}{2}} u_{0} e^{i\left(k_{x} \xi+k_{y} \eta\right)} e^{-i \frac{k}{f^{\prime}}\left(x^{\prime} \xi+y^{\prime} \eta\right)} d \eta \\
& \propto \int_{-\frac{a}{2}}^{\frac{a}{2}} e^{i \xi\left(k_{x}-k \frac{x^{\prime}}{f^{\prime}}\right)} d \xi \int_{-\frac{b}{2}}^{\frac{b}{2}} e^{i \eta\left(k_{y}-k \frac{y^{\prime}}{f^{\prime}}\right)} d \eta
\end{aligned}
\]
cuyo resultado es1
\[
\hat{u}\left(x^{\prime}, y^{\prime}\right) \propto 4 \operatorname{sinc}\left[\left(k_{x}-k \frac{x^{\prime}}{f^{\prime}}\right) \frac{a}{2}\right] \times \operatorname{sinc}\left[\left(k_{y}-k \frac{y^{\prime}}{f^{\prime}}\right) \frac{b}{2}\right] \notag
\]
nos interesa la intensidad (proporcional al cuadrado del campo)
\[
\begin{aligned}
I\left(x^{\prime}, y^{\prime}\right)=& I(0,0) \operatorname{sinc}^{2}\left[\left(k_{x}-k \frac{x^{\prime}}{f^{\prime}}\right) \frac{a}{2}\right] \\
& \times \operatorname{sinc}^{2}\left[\left(k_{y}-k \frac{y^{\prime}}{f^{\prime}}\right) \frac{b}{2}\right]
\end{aligned}
\]
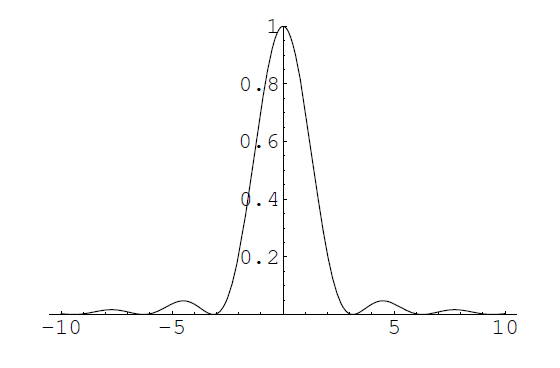
donde la constante \(I(0,0)\) lleva todas las constantes omitidas en la integración. Para hacernos una idea de cómo es la distribución de intensidades, podemos ver la figura. Constatamos lo siguiente
- Es similar a la función de BesseL \(J_{1}\) obtenida para la abertura circular.
- Veremos el primer máximo y, a lo mejor, el segundo, pero poco más, ya que la intensidad decrece rápidamente.
- La imagen que veremos en el plano focal imagen es como la de la figura. Podemos estimar el tamaño en función del tamaño del máximo central en cada una de las direcciones.
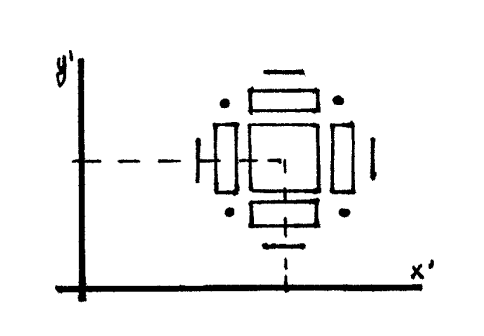
- En la dirección \(x^{\prime}\) las coordenadas \(x_{1}^{\prime}\) del cero que limita al máximo central por la derecha y \(x_{-1}^{\prime}\) del que lo limita por la izquierda son, respectivamente:
\[
\begin{aligned}
&\left(k_{x}-k \frac{x_{1}^{\prime}}{f^{\prime}}\right) \frac{a}{2}=\pi \\
&\left(k_{x}-k \frac{x_{-1}^{\prime}}{f^{\prime}}\right) \frac{a}{2}=-\pi
\end{aligned}
\]
por lo que el tamaño del máximo central en la dirección \(x^{\prime}\) resulta ser
\[
\begin{aligned}
\Delta x &=\left|x_{1}^{\prime}-x_{-1}^{\prime}\right| \\
&=\frac{2 f^{\prime} \lambda}{a}
\end{aligned}
\]
- En la dirección \(y^{\prime}\) los cálculos son análogos, y su resultado es
\[
\Delta y=\frac{2 f^{\prime} \lambda}{b} \notag
\]
- Todo lo que es apartamiento de la óptica geométrica (es decir, de la imagen puntual) es lo que llamamos difracción.
- En cuanto al tamaño de la figura de difracción, crece linealmente con \(\lambda\) y es inversamente proporcional al tamaño de la abertura, al igual que sucedía para la abertura circular.
_____________________________________________________________
1. recordemos que se define el seno cardinal del ángulo \(\phi\) como sinc \((\phi)=\frac{\sin \phi}{\phi}\). 10 Difracción

