5.4: Coherencia

En la discusión hasta el momento sólo hemos considerado la luz monocromática, lo que significa que el espectro de la luz consiste en una sola frecuencia. Aunque la luz de un láser suele tener una banda de frecuencias muy estrecha y por lo tanto puede considerarse monocromática, la luz puramente monocromática no existe. Toda la luz consiste en múltiples frecuencias y por lo tanto es policromática. Las fuentes de luz clásicas como las lámparas incandescentes y también los LED tienen bandas de frecuencia relativamente amplias. Entonces surge la pregunta de cuán diferente se comporta la luz policromática en comparación con el caso idealizado de la luz monocromática. Para responder a esta pregunta, debemos estudiar el tema de la coherencia. Se distingue entre dos extremos: la luz totalmente coherente y totalmente incoherente, mientras que el grado de coherencia de la luz práctica está en algún punto intermedio. En términos generales, cuanto más amplia es la banda de frecuencia de la fuente, más incoherente es la luz. Es una observación muy importante que ninguna luz es en realidad completamente coherente o completamente incoherente. Toda la luz es parcialmente coherente, pero alguna luz es más coherente que otras.

Una manera intuitiva de pensar sobre estos conceptos es en términos de la capacidad de formar franjas de interferencia. Por ejemplo, con la luz láser, que suele ser casi monocromática y por lo tanto coherente, se puede formar un patrón de interferencia con máximos y mínimos claros en intensidades (las llamadas franjas) utilizando una doble hendidura, mientras que con la luz solar (que es incoherente) esto es mucho más difícil. Cada frecuencia en el espectro de la luz solar da su propio patrón de interferencia con su propio patrón de franja dependiente de la frecuencia. Estos patrones de flecos se lavan debido a la superposición y la intensidad total, por lo tanto, muestra poco contraste de franjas, es decir, la coherencia es menor. Sin embargo, no es imposible crear franjas de interferencia con la luz natural. El truco es dejar que las dos rendijas estén tan juntas (del orden de\(0.02 \mathrm{~mm}\)) que la diferencia en distancias desde las rendijas hasta el sol sea tan pequeña para que los campos en las rendijas sean lo suficientemente coherentes como para interferir. Para entender el efecto de la luz policromática, es esencial entender que el grado en que los campos en dos puntos son coherentes, es decir, la capacidad de formar franjas, está determinado por la diferencia de distancias entre estos puntos y la fuente. La distancia en sí misma a la fuente no es relevante. En las siguientes secciones estudiamos estos temas de manera más cuantitativa.

5.3.1 Coherencia de las fuentes de luz

En una fuente de luz convencional como una lámpara de descarga de gas, los fotones son generados por transiciones electrónicas en los átomos del gas. Estas transiciones tienen una duración del orden de\(10^{-8}\) a\(10^{-9} \mathrm{~s}\). Debido a que los trenes de ondas emitidos son finitos, la luz emitida no tiene una sola frecuencia; en cambio, hay una banda de frecuencias alrededor de una frecuencia central. Esta dispersión de frecuencias se llama el ancho de línea natural. Los movimientos térmicos aleatorios de las moléculas provocan un mayor ensanchamiento debido al efecto Doppler. Además, los átomos sufren colisiones que interrumpen los trenes de ondas y por lo tanto amplían aún más el espectro de frecuencias.

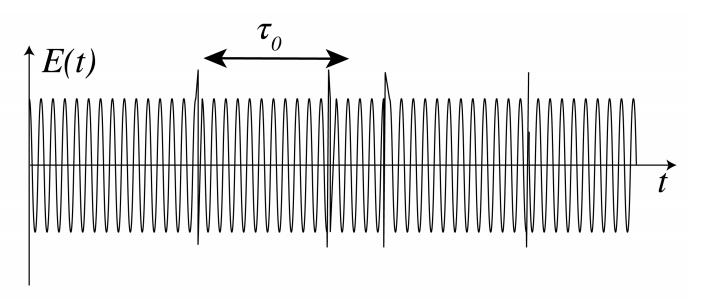
Primero consideramos un solo átomo emisor. Cuando las colisiones son el efecto de ensanchamiento dominante y estas colisiones son suficientemente breves, de modo que se pueda ignorar cualquier radiación emitida durante la colisión, un modelo preciso para la onda emitida es un tren de ondas monocromáticas constantes a frecuencia\(\bar{\omega}\) en el centro de la banda de frecuencias, interrumpido por saltos de fase aleatorios cada vez que ocurre una colisión. Las discontinuidades en la fase debido a las colisiones provocan una dispersión de frecuencias alrededor de la frecuencia central. Un ejemplo se muestra en la Figura\(\PageIndex{1}\). El tiempo promedio\(\tau_{0}\) entre las colisiones es típicamente inferior a 10 ns, lo que implica que en promedio entre dos colisiones ocurren aproximadamente 150,000 oscilaciones armónicas. El tiempo de coherencia\(\Delta \tau_{c}\) se define como el intervalo de tiempo máximo durante el cual se puede predecir la fase del campo eléctrico. En el caso de la emisión dominada por colisiones por un solo átomo, el tiempo de coherencia es igual al tiempo promedio entre colisiones posteriores:\(\Delta \tau_{c}=\tau_{0}\).

Para entender la coherencia y la incoherencia, es muy útil utilizar este modelo para la emisión por un solo átomo como trenes de ondas armónicas de miles de periodos interrumpidos por saltos de fase aleatorios. El tiempo de coherencia y el ancho\(\Delta \omega\) de la línea de frecuencia se relacionan como

Figura\(\PageIndex{1}\): La amplitud del campo eléctrico del tren de ondas armónicas irradiado por un solo átomo en la frecuencia central\(\bar{\omega}\). Las líneas verticales son colisiones separadas por periodos de vuelo libre con duración media\(\tau_{0}\). La cantidad\(\bar{\omega} \tau_{0}\), que es el número de periodos en un tren de olas típico, se elige de manera poco realista (es decir, 60, mientras que un valor realista lo sería\(10^{5}\)), para mostrar los cambios de fase aleatorios.

\[\Delta \tau_{c}=\frac{2 \pi}{\Delta \omega} \nonumber \]

La longitud de coherencia se define por\[\Delta \ell_{c}=c \Delta \tau_{c} . \nonumber \]

Ya que\(\lambda \omega=2 \pi c\), tenemos\[\frac{\Delta \lambda}{\bar{\lambda}}=\frac{\Delta \omega}{\bar{\omega}}, \nonumber \] dónde\(\lambda\) y\(\bar{\omega}\) están la longitud de onda y la frecuencia en el centro de la línea. Por lo tanto,\[\Delta \ell_{c}=c \frac{2 \pi}{\Delta \omega}=2 \pi \frac{c}{\bar{\omega}} \frac{\bar{\omega}}{\Delta \omega}=\frac{\bar{\lambda}^{2}}{\Delta \lambda} \nonumber \]

La duración de coherencia y el tiempo de coherencia de una serie de fuentes se enumeran en la Tabla\(\PageIndex{1}\).

Tabla\(\PageIndex{1}\): Tiempo de coherencia y duración de varias fuentes

Fuente	Longitud de onda media	Ancho de línea	Longitud de coherencia	Tiempo de Coherencia
	\(\bar{\lambda}\)	\(\Delta \lambda\)	\(\bar{\lambda}^{2} / \Delta \lambda\)	\(\frac{\bar{\lambda}}{\Delta \lambda} \frac{\bar{\lambda}}{c}\)
IR medio (3-5\(\mu \mathrm{m}\))	\(4.0 \mu \mathrm{m}\)	\(2.0 \mu \mathrm{m}\)	\(8.0 \mu \mathrm{m}\)	\(2.66 \times 10^{-14} \mathrm{~s}\)
Luz blanca	\(550 \mathrm{~nm}\)	\(\approx 300 \mathrm{~nm}\)	\(\approx 900 \mathrm{~nm}\)	\(\approx 3.0 \times 10^{-14} \mathrm{~s} .\)
Arco de Mercurio	\(546.1 \mathrm{~nm}\)	\(\approx 1.0 \mathrm{~nm}\)	\(\approx 0.3 \mathrm{~mm}\)	\(\approx 1.0 \times 10^{-12} \mathrm{~s} .\)
Lámpara de\(^{86}\) descarga Kr	\(605.6 \mathrm{~nm}\)	\(1.2 \times 10^{-3} \mathrm{~nm}\)	\(0.3 \mathrm{~m}\)	\(1.0 \times 10^{-9} \mathrm{~s} .\)
Láser He-Ne estabilizado	\(632.8 \mathrm{~nm}\)	\(\approx 10^{-6} \mathrm{~nm}\)	\(400 \mathrm{~m}\)	\(1.33 \times 10^{-6}\)s.

5.3.2 Luz policromática

Cuando se trata de coherencia hay que considerar campos que constan de un rango de frecuencias diferentes. Dejar\(\mathcal{U}(\mathbf{r}, t)\) ser el componente de campo físico de valor real. Siempre es posible escribir\(\mathcal{U}(\mathbf{r}, t)\) como una integral sobre componentes armónicos de tiempo:\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} \int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega, \nonumber \] donde\(A_{\omega}(r)\) está la amplitud compleja del campo armónico de tiempo con frecuencia\(\omega\). Cuando sólo hay una cierta banda de frecuencias que aporta, entonces\(A_{\omega}=0\) para\(\omega\) fuera de esta banda. Definimos el complejo campo dependiente del tiempo\(U(\mathbf{r}, t)\) por\[U(\mathbf{r}, t)=\int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega . \nonumber \]

Entonces\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t) \nonumber \]

Observación: El campo complejo\(U(\mathbf{r}, t)\) contiene ahora la dependencia del tiempo en contraste con la notación utilizada para un campo armónico de tiempo (es decir, frecuencia única) introducido en el Capítulo 2, donde el dependiente del tiempo\(e^{-i \omega t}\) era un factor separado.

Campo cuasi-monocromático. Si el ancho\(\Delta \omega\) de la banda de frecuencia es muy estrecho, hablamos de vuelo cuasi-monocromático. En la propagación de campos cuasi-monocromáticos, utilizamos la fórmula para campos armónicos de tiempo en la frecuencia central\(\bar{\omega}\). La suposición cuasi-monocromática simplifica considerablemente los cálculos. Sin embargo, la mayor parte del tratamiento que sigue es más general y no supone que el campo sea cuasi-monocromático.

Ahora calculamos la intensidad de la luz policromática. El flujo de energía instantáneo es (como para la luz monocromática) proporcional al cuadrado del campo real instantáneo:\(\mathcal{U}(\mathbf{r}, t)^{2}\). Se promedia la intensidad instantánea a lo largo del tiempo\(T\) de integración de detectores comunes que, como se indicó anteriormente, es muy larga en comparación con el periodo en la frecuencia central\(2 \pi / \bar{\omega}\) del campo (al menos\(10^{5}\) veces el periodo de la luz). Usando definición (5.2.6) y\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t)=\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right) / 2, \nonumber \] obtenemos\[\begin{aligned} \left\langle\mathcal{U}(\mathbf{r}, t)^{2}\right\rangle &=\frac{1}{4}\left\langle\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\right\rangle \\ &=\frac{1}{4}\left\{\left\langle U(\mathbf{r}, t)^{2}\right\rangle+\left\langle\left(U(\mathbf{r}, t)^{*}\right)^{2}\right\rangle+2\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle\right\} \\ &=\frac{1}{2}\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle \\ &=\frac{1}{2}\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \end{aligned} \nonumber \] donde los promedios de\(U(\mathbf{r}, t)^{2}\) y\(\left(U(\mathbf{r}, t)^{*}\right)^{2}\) son cero porque son funciones de oscilación rápida del tiempo. Por el contrario,\(|U(\mathbf{r}, t)|^{2}=U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\) tiene un componente de CC que no tiene un promedio de cero.

Observación: En contraste con el caso armónico de tiempo, el promedio de largo tiempo de la luz policromática depende del tiempo\(t\) en que se tome el promedio. No obstante, asumimos en este capítulo que los campos son omitidos por fuentes que son estacionarias. La propiedad de estacionariedad implica que el promedio a lo largo del intervalo de tiempo de larga duración\(T\) no depende del tiempo que se tome el promedio. Muchas fuentes de luz, en particular los láseres convencionales, son estacionarias. (Sin embargo, una fuente láser que emite pulsos cortos de alta potencia no puede considerarse como una fuente estacionaria). Además, asumimos que los campos son ergódicos, lo que significa que tomar el promedio de tiempo en un intervalo de tiempo largo equivale a tomar el promedio sobre el conjunto de campos posibles. Se puede demostrar que esta propiedad implica que el límite\(T \rightarrow \infty\) en (5.2.6) efectivamente existe.

Utilizamos para la intensidad nuevamente la expresión sin el factor al frente, es decir\[I(\mathbf{r})=\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \nonumber \] La intensidad promediada\(1 / 2\) en el tiempo se ha expresado en términos del promedio de tiempo del módulo cuadrado del campo complejo.