7.3: Amplificación

La amplificación se puede lograr mediante un medio con resonancias atómicas que están en o cerca de una de las resonancias del resonador. Primero recordamos la teoría simple desarrollada por Einstein en 1916 del equilibrio dinámico de un material en presencia de radiación electromagnética.

7.3.1 Los coeficientes de Einstein

Consideramos dos niveles de energía atómica$E_{2}>E_{1}$. Al absorber un fotón de energía,

$$\hbar \omega=E_{2}-E_{1}, \nonumber$$ un átomo que inicialmente se encuentra en el estado de energía inferior 1 puede excitarse al estado 2. Aquí$\hbar$ está la constante de Planck: $$\hbar=\frac{6.626070040}{2 \pi} \times 10^{-34} \quad \text { Js } . \nonumber$$

Supongamos$W(\omega)$ es la densidad de energía electromagnética promediada en el tiempo por unidad de intervalo de frecuencia alrededor de la frecuencia$\omega$ De ahí$W$ que tenga dimensión Jsm$^{3}$. Let$N_{1}$ y$N_{2}$ ser el número de átomos en estado 1 y 2, respectivamente, donde

$$N_{1}+N_{2}=N, \nonumber$$ está el número total de átomos (que es constante). La tasa de absorción es la tasa de disminución de$N_{1}$ y es proporcional a la densidad de energía y al número de átomos en el estado 1: $$\frac{d N_{1}}{d t}=-B_{12} N_{1} W(\omega), \quad \text { absorption, } \nonumber$$ donde la constante$B_{12}>0$ tiene dimensión$\mathrm{m}^{3} \mathrm{~J}^{-1} \mathrm{~s}^{-2}$. Sin ninguna influencia externa, un átomo que se encuentra en el estado excitado generalmente se transferirá al estado 1 dentro$1 \mathrm{~ns}$ o así, mientras emite un fotón de energía (7.10). Este proceso se denomina emisión espontánea, ya que ocurre también sin un campo electromagnético presente. La tasa de emisión espontánea viene dada por: $$\frac{d N_{2}}{d t}=-A_{21} N_{2}, \quad \text { spontaneous emission, } \nonumber$$ donde$A_{21}$ tiene dimensión$\mathrm{s}^{-1}$. La vida útil de la transmisión espontánea es$\tau_{s p}=1 / A_{21}$. Es importante señalar que el fotón espontáneamente emitido se emite en una dirección aleatoria. Además, dado que la radiación se produce en un tiempo aleatorio, no existe relación de fase entre el campo espontáneamente emitido y el campo que excita al átomo.

Es menos obvio que ante la presencia de un campo electromagnético de frecuencia cercano a la resonancia atómica, un átomo en estado excitado también puede ser estimulado por ese campo para emitir un fotón y transferirse al estado de energía inferior. La tasa de emisión estimulada es proporcional al número de átomos excitados y a la densidad de energía del campo:

$$\frac{d N_{2}}{d t}=-B_{21} N_{2} W(\omega), \quad \text { stimulated emission, } \nonumber$$ donde$B_{21}$ tiene la misma dimensión que$B_{12}$. Es muy importante señalar que la emisión estimulada se produce en el mismo modo electromagnético (por ejemplo, una onda plana) que el modo del campo que excita la transmisión y que la fase del campo radiado es idéntica a la del campo excitante. Esto implica que la emisión estimulada potencia el campo electromagnético por interferencia constructiva. Esta propiedad es crucial para el funcionamiento del láser.

7.3.2 Relación entre los coeficientes de Einstein

Existen relaciones entre los coeficientes de Einstein$A_{21}, B_{12}$ y$B_{21}$. Considera un cuerpo negro, como una caja vacía cerrada. Después de cierto tiempo, se alcanzará el equilibrio térmico. Debido a que no hay radiación que ingrese a la caja desde el exterior ni salga de la caja hacia el exterior, la densidad de energía electromagnética es la densidad$W_{T}(\omega)$ térmica, la cual, según la Ley de Planck, es independiente del material del que está hecha la caja y viene dada por:

$$W_{T}(\omega)=\frac{\hbar \omega^{3}}{\pi^{2} c^{3}} \frac{1}{\exp \left(\frac{\hbar \omega}{k_{B} T}\right)-1}, \nonumber$$ donde $k_{B}$es la constante de Boltzmann: $$k_{B}=1.38064852 \times 10^{-23} \mathrm{~m}^{2} \mathrm{kgs}^{-2} \mathrm{~K}^{-1} . \nonumber$$

Figura$\PageIndex{1}$: Absorción, emisión espontánea y emisión estimulada.

La velocidad de transición ascendente y descendente de los átomos en la pared de la caja debe ser idéntica:

$$B_{12} N_{1} W_{T}(\omega)=A_{21} N_{2}+B_{21} N_{2} W_{T}(\omega) . \nonumber$$

Por lo tanto,

$$W_{T}(\omega)=\frac{A_{21}}{B_{12} N_{1} / N_{2}-B_{21}} . \nonumber$$

Pero en equilibrio térmico:

$$\frac{N_{2}}{N_{1}}=\exp \left(-\frac{E_{2}-E_{1}}{k_{B} T}\right)=\exp \left(-\frac{\hbar \omega}{k_{B} T}\right) . \nonumber$$

Al sustituir ($\PageIndex{11}$) en ($\PageIndex{10}$) y comparar el resultado con ($\PageIndex{7}$), se deduce que ambas expresiones para$W_{T}(\omega)$ son idénticas para todas las temperaturas solo si

$$B_{12}=B_{21}, \quad A_{21}=\frac{\hbar \omega^{3}}{\pi^{2} c^{3}} B_{21} . \nonumber$$

Ejemplo Para luz verde de$\lambda=550 \mathrm{~nm}$, tenemos$\omega / c=2 \pi / \lambda=2.8560 \times 10^{6} \mathrm{~m}^{-1}$ y por lo tanto

$$\frac{A_{21}}{B_{21}}=1.5640 \times 10^{-15} \mathrm{~J} \mathrm{~s} \mathrm{~m}^{-3} . \nonumber$$

De ahí que las tasas de emisión espontánea y estimulada sean iguales si$W(\omega)=1.5640 \times 10^{-15} \mathrm{Js} \mathrm{m}^{-3}$

Para una banda de frecuencia (estrecha),$\mathrm{d} \omega$ la densidad de energía promediada en el tiempo es$W(\omega) \mathrm{d} \omega$ y para una onda plana la densidad de energía está relacionada con la intensidad$I$ (es decir, la longitud del vector Poynting promediado en el tiempo) como:

$$W(\omega) \mathrm{d} \omega=I / c . \nonumber$$

Cuadro$\PageIndex{1}$: Intensidades típicas de fuentes de luz.

	$I\left(\mathrm{~W} \mathrm{~m}^{-2}\right)$
Lámpara Mercury	$10^{4}$
Láser continuo	$10^{5}$
Láser pulsado	$10^{13}$

Un valor típico para el ancho de frecuencia de una línea de emisión estrecha de una fuente de luz ordinaria es:$10^{10} \mathrm{~Hz}$, i.e$\mathrm{d} \omega=2 \pi \times 10^{10} \mathrm{~Hz}$. De ahí que las tasas de emisión espontánea y estimulada sean idénticas si la intensidad es$I=2.95 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}$. Como se ve en el Cuadro 7.1, solo para la emisión estimulada por luz láser es mayor que la emisión espontánea. Para las fuentes de luz clásicas, la tasa de emisión espontánea es mucho mayor que la tasa de emisión estimulada. Si un haz con ancho de frecuencia$\mathrm{d} \omega$ y densidad de energía$W(\omega)$ d$\omega$ se propaga a través de un material, la tasa de pérdida de energía es proporcional a:

$$\left(N_{1}-N_{2}\right) B_{12} W(\omega) . \nonumber$$

Según ($\PageIndex{9}$) esto es igual a la tasa de emisión espontánea. En efecto, la luz emitida espontáneamente corresponde a una pérdida de intensidad del haz, debido a que se emite en direcciones aleatorias y con fase aleatoria.

Cuando$N_{2}>N_{1}$, la luz se amplifica. A este estado se le llama inversión poblacional y es fundamental para el funcionamiento del láser. Obsérvese que la relación de las tasas de emisión espontánea y estimulada es, según ($\PageIndex{12}$), proporcional a$\omega^{3}$. Por lo tanto, para longitudes de onda más cortas como$\mathrm{x}$ los rayos, es mucho más difícil hacer láseres que para la luz visible.

7.3.3 Inversión poblacional

Para la densidad de energía electromagnética$W(\omega)$ por unidad de intervalo de frecuencia, las ecuaciones de velocidad son

$$\begin{aligned} \frac{d N_{2}}{d t} &=-A_{21} N_{2}+\left(N_{1}-N_{2}\right) B_{12} W(\omega) \\ \frac{d N_{1}}{d t} &=A_{21} N_{2}-\left(N_{1}-N_{2}\right) B_{12} W(\omega) \end{aligned} \nonumber$$

De ahí, para$\Delta N=N_{2}-N_{1}$:

$$\frac{d \Delta N}{d t}=-A_{21} \Delta N-2 \Delta N B_{12} W(\omega)-A_{21} N \nonumber$$ donde como antes:$N=N_{1}+N_{2}$ es constante. Si inicialmente (es decir, en$t=0$) todos los átomos están en el estado más bajo:$\Delta N(t=0)=-N$, entonces se deduce de$\PageIndex{12}$: $$\Delta N(t)=-N\left[\frac{A_{21}}{A_{21}+2 B_{12} W(\omega)}+\left(1-\frac{A_{21}}{A_{21}+2 B_{12} W(\omega)}\right) e^{-\left(A_{21}+2 B_{12} W(\omega)\right) t}\right] \nonumber$$

Un ejemplo donde$A_{21} / B_{12} W(\omega)=0.5$ se muestra en la Figura$\PageIndex{2}$. Siempre tenemos$\Delta N<0$, de ahí$N_{2}(t)<N_{1}(r)$ para todos los tiempos$t$. Por lo tanto, un sistema con sólo dos niveles no puede tener inversión poblacional.

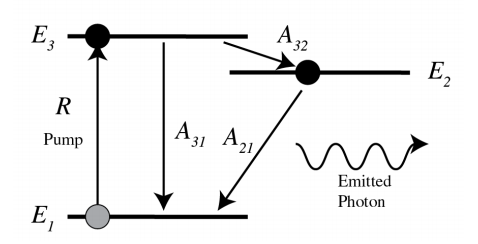
Una manera de lograr la inversión poblacional de los niveles 1 y 2 y de ahí la amplificación de la radiación$\omega$ con frecuencia con$\hbar \omega=E_{2}-E_{1}$ es utilizar niveles más atómicos, por ejemplo tres. En$\PageIndex{3}$ la Figura el estado fundamental es el estado 1 con dos niveles superiores 2 y 3 tal que$E_{1}<E_{2}<E_{3}$. La transición de interés sigue siendo la del nivel 2 al nivel 1. Inicialmente casi todos los átomos están en el estado fundamental 1. Entonces los átomos se bombean con velocidad$R$ desde el nivel 1 directamente al nivel 3. La transición$3 \rightarrow 2$ es no radiativa y tiene una tasa alta$A_{32}$ por lo que el nivel 3 se vacía rápidamente y por lo tanto$N_{3}$ permanece pequeño. El estado 2 se denomina estado metaestable, porque el tiempo de residencia en el estado metaestable es para cada átomo relativamente largo. Por lo tanto, su población tiende a aumentar, lo que lleva a una inversión poblacional entre el estado metaestable 2 y el estado fundamental inferior 1 (el cual se está despoblando continuamente bombeando al nivel más alto).

Tenga en cuenta que$A_{31}$ tiene que ser pequeño, porque de lo contrario se llenará rápidamente el nivel 1, por lo que se detendrá la inversión poblacional. Este efecto puede ser utilizado para obtener una serie de pulsos láser como salida, pero no es deseable para una potencia de salida continua.

Figura$\PageIndex{2}$:$\Delta N / N$ como función de$t /\left(A_{21}+2 B_{12} W\right)$ cuando todos los átomos están en el estado fundamental en$t=0$, i.e$\Delta N(0)=-N$.

El bombeo puede realizarse ópticamente como se describe, pero la energía para transferir átomos del nivel 1 al nivel 3 también puede ser suministrada por una descarga eléctrica en un gas o por una corriente eléctrica. Después de que el bombeo haya logrado inversión poblacional, inicialmente no se emite luz. Entonces, ¿cómo comienza realmente el láser? El láser comienza por emisión espontánea. Los fotones espontáneamente emitidos estimulan la emisión de los átomos en el nivel 2 para desintegrarse al nivel 1, mientras emiten un fotón de energía$\hbar \omega$. Esta emisión estimulada ocurre en fase con la luz excitante y por lo tanto la luz se acumula continuamente de manera coherente, mientras rebota de un lado a otro entre los espejos del resonador. Uno de los espejos es ligeramente transparente y de esta manera parte de la luz se escapa del láser.

Figura$\PageIndex{3}$: Las tres transiciones de Einstein y la bomba.