1.7: El arco iris

No sé la forma exacta de una gota de lluvia, ¡pero dudo mucho si es en forma de gota! La mayoría de las gotas de lluvia serán más o menos esféricas, especialmente las gotas pequeñas, debido a la tensión superficial. Si las gotas grandes que caen se distorsionan a partir de una forma esférica exacta, imagino que es más probable que se aplanen a una especie de forma de panqueque horizontal en lugar de en forma de gota. Independientemente, en el análisis de esta sección, asumiré que las gotas son esféricas, como estoy seguro que serán las gotas pequeñas.

Deseamos seguir un rayo de luz a medida que entra en una gota esférica, se refleja internamente y finalmente emerge. Ver Figura I.15. Nos referiremos a la distancia\(b\) como parámetro de impacto.

Vemos un rayo de luz dirigido a la gota, que tomo para tener radio unitario, en parámetro de impacto\(b\). La desviación de la dirección del rayo emergente de la dirección del rayo incidente es

\[D = \theta - \theta' + \pi -2\theta' +\theta - \theta' = \pi + 2\theta - 4\theta'. \label{eq:1.7.1} \]

No obstante, nos interesará más el ángulo\(r = \pi − D\). Un rayo de luz que se ha desviado se\(D\) acercará al observador desde una dirección que forma un ángulo\(r\) desde el centro de la proa, que se encuentra en el punto antisolar (Figura I.16)

Nos gustaría encontrar la desviación\(D\) en función del parámetro de impacto. Los ángulos de incidencia y refracción están relacionados con el parámetro de impacto de la siguiente manera:

\[\sin\theta=b,\label{eq:1.7.2} \]

\[\cos\theta=\sqrt{1-b^2},\label{eq:1.7.3} \]

\[\sin\theta' = b/n,\label{eq:1.7.4} \]

y

\[ \cos\theta = \sqrt{1-b^2/n^2}. \label{eq:1.7.5} \]

Estos, junto con la Ecuación\(\ref{eq:1.7.1}\), nos dan la desviación en función del parámetro de impacto. La desviación pasa por un mínimo —y\(r\) pasa por un máximo. La desviación para un parámetro de rayo de luz de impacto\(b\) es

\[D = \pi + 2\sin^{-1}b - 4\sin^{-1}(b/n)\label{eq:1.7.6} \]

La distancia angular\(r\) desde el centro de la proa es\(r = \pi − D\), de modo que

\[r = 4 \sin^{-1}(b/n) - 2\sin^{-1}b.\label{eq:1.7.7} \]

Esto se muestra en la Figura I.17 para\(n\) = 1.3439 (azul -\(\gamma\) = 400 nm) y\(n\) = 1.3316 (rojo -\(\gamma\) = 650 nm).

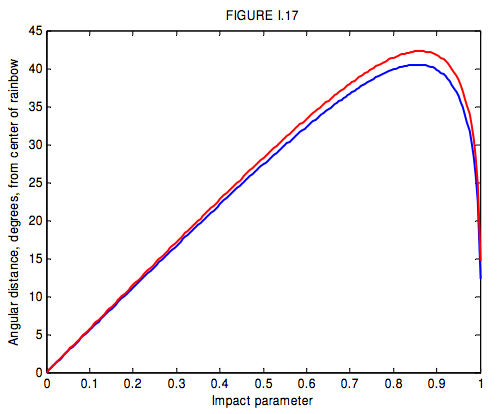
La diferenciación da el valor máximo,\(R\), de\(r\) - es decir, el radio de la proa- o la desviación mínima\(D_{\text{min}}\). Obtenemos para el radio de la proa

\[R = 4\sin^{-1}\sqrt{\frac{4-n^2}{3n^2}}- 2\sin^{-1}\sqrt{\frac{4-n^2}{3}}. \label{eq:1.7.8} \]

Para\(n\) = 1.3439 (azul) esto es 40 ° 31' y para\(n\) = 1.3316 (rojo) esto es 42 ° 17'. Así el azul está en el interior del arco, y el rojo en el exterior.

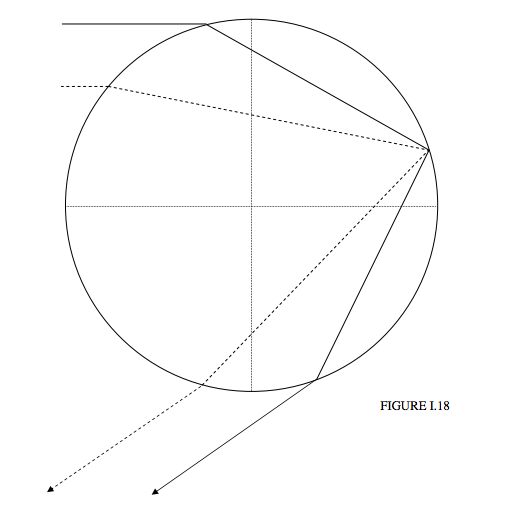
Para la incidencia de pastoreo (parámetro de impacto = 1), la desviación es\( 2 \pi -4 \sin^{-1}(1/n)\), o 167 ° 40' para el azul o 165 ° 18' para el rojo. Esto corresponde a una distancia del centro del arco\( r = 4 \sin^{-1}(1/n)-\pi\), que es '12 ° 20' para el azul y 14 ° 42' para el rojo. Se verá de la figura I.17 que para radios menores que\(R\) (es decir, dentro del arco iris) pero mayores a 12 ° 20' para el azul y 14 ° 42' para el rojo hay dos parámetros de impacto que dan como resultado la misma desviación, es decir, en la misma posición dentro del arco. Las trayectorias de dos rayos con la misma desviación se muestran en la Figura I.18. Un rayo se dibuja como una línea completa, el otro como una línea discontinua. Comienzan con diferentes parámetros de impacto, y toman diferentes caminos a través de la caída, pero terminan en la misma dirección. El dibujo se realiza para una desviación de 145 °, o 35 ° del centro de proa. Los dos parámetros de impacto son 0.969 y 0.636. Cuando estos dos rayos se recombinan al ser llevados a un foco en la retina del ojo, han satisfecho todas las condiciones de interferencia, y el resultado será brillo u oscuridad según si la diferencia de trayectoria es un número par o impar de medias longitudes de onda.

Si miras justo dentro del margen interior (azul) del arco, a menudo puedes ver claramente las franjas de interferencia producidas por dos rayos con la misma desviación. No lo he intentado, pero si tuvieras que mirar a través de un filtro que transmita un solo color, estas franjas (si son lo suficientemente brillantes como para ver) deberían estar bien definidas. La diferencia de trayectoria óptica para una desviación dada, o dada\(r\), depende del radio de la caída (y de su índice de refracción). Para una caída de radio\(a\) es fácil ver que la diferencia de trayectoria óptica es

\( 2a(\cos\theta_2 - \cos\theta_1) - 4n(\cos\theta'_2-\cos\theta'_1),\)

donde\(\theta_1\) es el mayor de los dos ángulos de incidencia. Presumiblemente, si tuvieras que medir el espaciado de franjas, podrías determinar el tamaño de las gotas. O bien, si realizaras un análisis de Fourier de la visibilidad de las franjas, podrías determinar, al menos en principio, la distribución del tamaño de las gotas.

A cierta distancia fuera del arco iris primario, hay un arco iris secundario, con colores invertidos, es decir, rojo en el interior, azul en el exterior. Esta está formada por dos reflexiones internas dentro de la gota (Figura I.19). La desviación del rayo emergente final de la dirección del rayo incidente es\((\theta − \theta') + (π − 2\theta') + (π − 2\theta') + (\theta − \theta')\), o en sentido contrario a\(2π + 2\theta − 6\theta'\) las agujas del reloj, que equivale a\(D = 6\theta' − 2\theta\) las agujas del reloj. Es decir,

\[ D = 6\sin^{-1}(b/n)-2\sin^{-1}b. \label{eq:1.7.9} \]

en sentido horario, y, como antes, esto corresponde a una distancia angular desde el centro de la proa\(r = \pi − D\). Muestro en la Figura I.20 la distancia angular desde el centro de la proa versus el parámetro de impacto\(b\). Observe que\(D\) pasa por un máximo y por lo tanto\(r\) tiene un valor mínimo. No hay luz dispersada fuera del arco primario, ni luz dispersada dentro del arco secundario. Cuando se observe toda la gloria de un arco primario y un arco secundario, se verá que el espacio entre los dos arcos es relativamente oscuro, mientras que es más brillante dentro del arco primario y fuera del arco secundario.

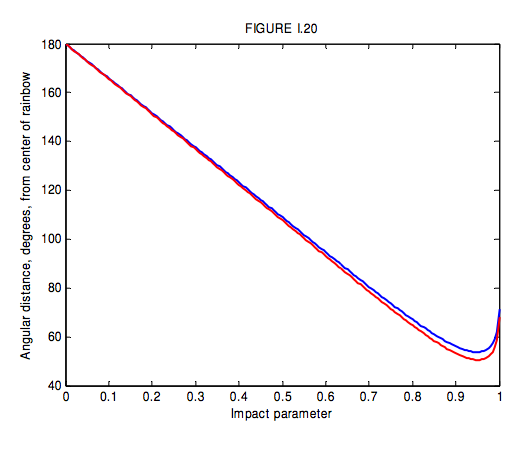
La diferenciación muestra que el menor valor de\(r\), (mayor desviación) correspondiente al radio del arco secundario es

\[R = 6\sin^{-1} \sqrt{\frac{3-n^2}{2n^2}} - 2\sin^{-1}\sqrt{\frac{3-n^2}{2}}\label{eq:1.7.10} \]

Para\(n = 1.3439\) (azul) esto es 53° 42' y para\(n = 1.3316\) (rojo) esto es 50° 31'. Así el rojo está en el interior del arco, y el azul en el exterior.

En principio es posible un arco terciario, involucrando tres reflexiones internas. No sé si alguien ha observado un arco terciario, pero me dicen que el arco primario es azul por dentro, el arco secundario es rojo por dentro, y “por lo tanto” el arco terciario sería azul por dentro. Por el contrario, afirmo que el arco terciario sería rojo por dentro. ¿Por qué es esto?

Volvamos a la proa primaria. La desviación es (Ecuación\(\ref{eq:1.7.1}\))\(D = π + 2\theta − 4\theta'\). Tomemos\(n = 4/3\), para lo que será en algún lugar en medio del espectro. Según la Ecuación\(\ref{eq:1.7.8}\), el radio de la proa\((R = \pi − D_{\text{min}})\) es entonces de aproximadamente 42°. Es decir,\(2\theta' − \theta\) = 21°. Si combinamos esto con la ley de Snell,\(3\sin \theta = 4\sin \theta'\), encontramos que, a desviación mínima (es decir, donde está el arco primario),\(\theta\) = 60°.5 y\(\theta'\) = 40°.8. Ahora, en el punto de reflexión interna, no toda la luz se refleja (porque\(\theta'\) es menor que el ángulo crítico de 36°.9), y se verá que el ángulo entre los rayos reflejados y refractados es (180 − 60.6 − 40.8) grados = 78°.6. Aquellos lectores que estén familiarizados con la ley de Brewster entenderán que cuando los rayos reflejados y transmitidos estén en ángulo recto entre sí, el rayo reflejado está completamente polarizado plano. El ángulo, como hemos visto, no es de 90°, sino de 78°.6, pero esto es lo suficientemente cercano a la condición de Brewster como para que la luz reflejada, aunque no esté completamente polarizada en plano, esté fuertemente polarizada. Así, como se puede verificar con un filtro polarizador, el arco iris está fuertemente polarizado plano.

Ahora quiero abordar la pregunta de cómo varía el brillo del arco de centro a circunferencia. Es más brillante donde la pendiente de la curva del parámetro de desviación versus impacto es menor, es decir, a desviación mínima (para el arco primario) o desviación máxima (para el arco secundario). De hecho, el resplandor (brillo superficial) a una distancia dada del centro del arco es (entre otras cosas) inversamente proporcional a la pendiente de esa curva. La situación se complica un poco ya que, para desviaciones entre\(D_{\text{min}}\) y\(2\pi - 4\sin^{-1}(1/n)\), (siendo esta última la desviación para la incidencia de pastoreo), hay dos parámetros de impacto que dan lugar a la misma desviación, pero para desviaciones mayores que esa (es decir, más cerca del centro de la proa) solo un impacto corresponde a una desviación dada.

Preguntémonos, por ejemplo, ¿qué tan brillante es el arco a 35° del centro (desviación 145°)? La desviación está relacionada con el parámetro de impacto por Ecuación\(\ref{eq:1.7.6}\). Para\(n = 4/3\), encontramos que los parámetros de impacto para desviaciones de 144, 145 y 146 grados son los siguientes:

D°	b
144	0.6583 y 0.9623
145	0.6366 y 0.9693
146	0.6157 y 0.9736

La Figura I.21 muestra una gota de lluvia vista desde la dirección de los fotones que se aproximan.

Cualquier fotón con parámetros de impacto dentro de los dos anulos oscuros se desviará entre 144° y 146°, y finalmente se acercará al observador a distancias angulares entre 36° y 34° del centro. El resplandor a una distancia de 35° del centro será proporcional, entre otras cosas, a la suma de las áreas de estos dos anales.

Yo he dicho “entre otras cosas”. Pensemos ahora en otras cosas. He dibujado la Figura I.15 como si toda la luz se transmitiera a medida que entra en la gota, y luego toda ella se refleja internamente dentro de la gota, y finalmente toda ella emerge cuando sale de la gota. Esto no es así, claro. En la entrada, en la reflexión interna y en la emergencia, parte de la luz se refleja y otra se transmite. Las fracciones que se reflejan o transmiten dependen del ángulo de incidencia, pero, para una desviación mínima, alrededor del 94% se transmite al entrar y nuevamente a la salida de la caída, pero solo alrededor del 6% se refleja internamente. También, después de la entrada, reflexión interna y salida, el porcentaje de polarización del rayo aumenta. Las fórmulas para los coeficientes de reflexión y transmisión (ecuaciones de Fresnel) son algo complicadas (las ecuaciones 1.5.1 y 1.5.2) son para luz incidente no polarizada), pero las he seguido en función del parámetro de impacto, y también he tenido en cuenta los tamaños de los uno o dos anulos involucrados para cada parámetro de impacto, y en consecuencia he calculado la variación del brillo de la superficie para un color\((n = 4/3)\) desde el centro hasta la circunferencia del arco. Omite los detalles de los cálculos, ya que este capítulo se planeó originalmente como un relato elemental de reflexión y transmisión, y parece que hemos ido un poco más allá de eso, pero muestro los resultados del cálculo en la Figura I.22. Sin embargo, no he tenido en cuenta los fenómenos de interferencia, que a menudo se pueden ver claramente justo dentro del arco primario.