3: La función integral exponencial

Tarde o temprano (en particular en el siguiente capítulo) en el estudio de las atmósferas estelares, tenemos necesidad de la función integral exponencial. Este breve capítulo no contiene nada sobre atmósferas estelares o incluso astronomía, sino que describe tanto como necesitamos saber sobre la función integral exponencial. No pretende ser una exposición minuciosa de todo lo que se pudiera escribir sobre la función.

La función integral exponencial del orden\(n\), escrita como una función de una variable\(a\), se define como

\[E_n(a) = \int_1^\infty x^{-n} e^{-ax} dx. \label{3.1}\]

Me limitaré a los casos en los\(n\) que sea un entero no negativo y\(a\) sea una variable real no negativa. Para la teoría de la atmósfera estelar en el siguiente capítulo tendremos necesidad de\(n\) hasta e incluyendo 3.

Empecemos por ver cuáles son los valores de las funciones cuando\(a = 0\). Tenemos

\[E_n (0) = \int_1^\infty x^{-n} dx \label{3.2}\]

y esto es infinito para\(n = 0\) y para\(n = 1\). Para mayor\(n\) es\(1/(n − 1)\).

Así\(E_0(0) = \infty\),\(E_1 (0) = \infty\),\(E_2 (0) = 1\)\(E_3(0) = \frac{1}{2}\),\(E_4(0) = \frac{1}{3}\),, etc.

A partir de entonces las funciones (de cualquier orden) disminuyen monótonamente a medida que\(a\) aumenta, acercándose a cero asintóticamente para grandes\(a\).

La función\(E_0(a)\) es fácil de evaluar. Es

\[E_0(a) = \int_1^\infty e^{-ax} dx = \frac{e^{-a}}{a}. \label{3.3}\]

La evaluación de la función integral exponencial para\(n > 0\) es menos fácil pero se puede hacer por integración numérica (e.g. Simpson). El límite superior de la integral en la ecuación 3.1 es infinito, pero esta dificultad se puede superar por medio de la sustitución\(y = 1/x\), a partir de la cual la ecuación se convierte

\[E_n(0) = \int_0^1 y^{n-2} e^{-a/y} dy. \label{3.4}\]

Dado que ambos límites son finitos, esto puede ahora en principio integrarse numéricamente de manera directa, por ejemplo mediante la regla de Simpson o algoritmo similar, excepto que, en el límite inferior,\(a/y\) es infinito y es necesario primero determinar el límite del integrando as\(y → 0\), que es cero.

Sin embargo, existe una manera de evaluar la función integral exponencial\(n ≥ 2\) sin necesidad de integración numérica. Consideremos, por ejemplo,

\[E_{n+1}(a) = \int_1^\infty x^{-(n+1)} e^{-ax} dx. \label{3.5}\]

Si esto está integrado (¡con mucho cuidado!) por partes, llegamos a

\[E_{n+1}(a) = \frac{1}{n} \left[ e^{-a} - aE_n (a) \right]. \label{3.6}\]

Así, a partir de esta relación de recurrencia, una vez que hemos evaluado\(E_1(a)\), podemos evaluar\(E_2(a)\) y por lo tanto\(E_3(a)\) y así sucesivamente.

La relación de recurrencia\(\ref{3.6}\), sin embargo, se mantiene solo para\(n ≥ 1\) (como se hará evidente durante la cuidadosa integración parcial), por lo que no hay forma de evitar la integración numérica para\(n = 1\). Además, para valores pequeños de\(a\) las funciones para\(n = 0\) o\(1\) llegar a ser muy grandes, llegando a ser infinitos como\(a → 0\), lo que las hace muy sensibles a la hora de intentar calcular la siguiente función hacia arriba. Así para pequeños\(a\) o para construir una mesa puede ser al final menos problema tomar el toro por los cuernos e integrarlos todos numéricamente.

Se permitirá una buena práctica de programación para preparar una mesa de\(E_n(a)\)\(a = 0\) para\(2\), en pasos de\(0.01\), para\(n = 0, 1, 2, 3\). La tabla debería tener idealmente cinco columnas, siendo la primera los\(201\) valores de\(a\), y siendo las cuatro restantes\(E_n(a)\),\(n = 1\) a\(4\). En la figura se muestra una gráfica de estas funciones\(\text{III.1}\).

En la práctica, al realizar los cálculos para la figura\(\text{III.1}\), esto es lo que encontré. La función para\(n = 0\) era fácil; viene dada simplemente por ecuación\(\ref{3.3}\). Porque\(n = 1\), integré por la regla de Simpson;\(100\) los intervalos en\(y\) fueron adecuados para computar la función a nueve decimales. La función para\(n = 2\) fue inesperadamente difícil. La relación de recurrencia no\(\ref{3.6}\) fue útil en pequeña medida\(a\), como se discutió anteriormente. Por lo tanto intenté integrarlo usando la regla de Simpson, sin embargo, aunque la función es, a primera vista, muy simple:

\[E_2(a) = \int_0^1 e^{-a/y} dy, \label{3.7} \]

La regla de Simpson parecía inadecuada para calcular la función precisamente incluso con tantos como\(1000\) intervalos en\(y\). ¡Ni la relación de recurrencia ni la integración numérica estuvieron sin problemas! No tuve dificultad, sin embargo, para integrar la función con\(n = 3\), y entonces usé la relación de recurrencia hacia atrás para calcular la función para\(n = 2\) y todo estaba bien.

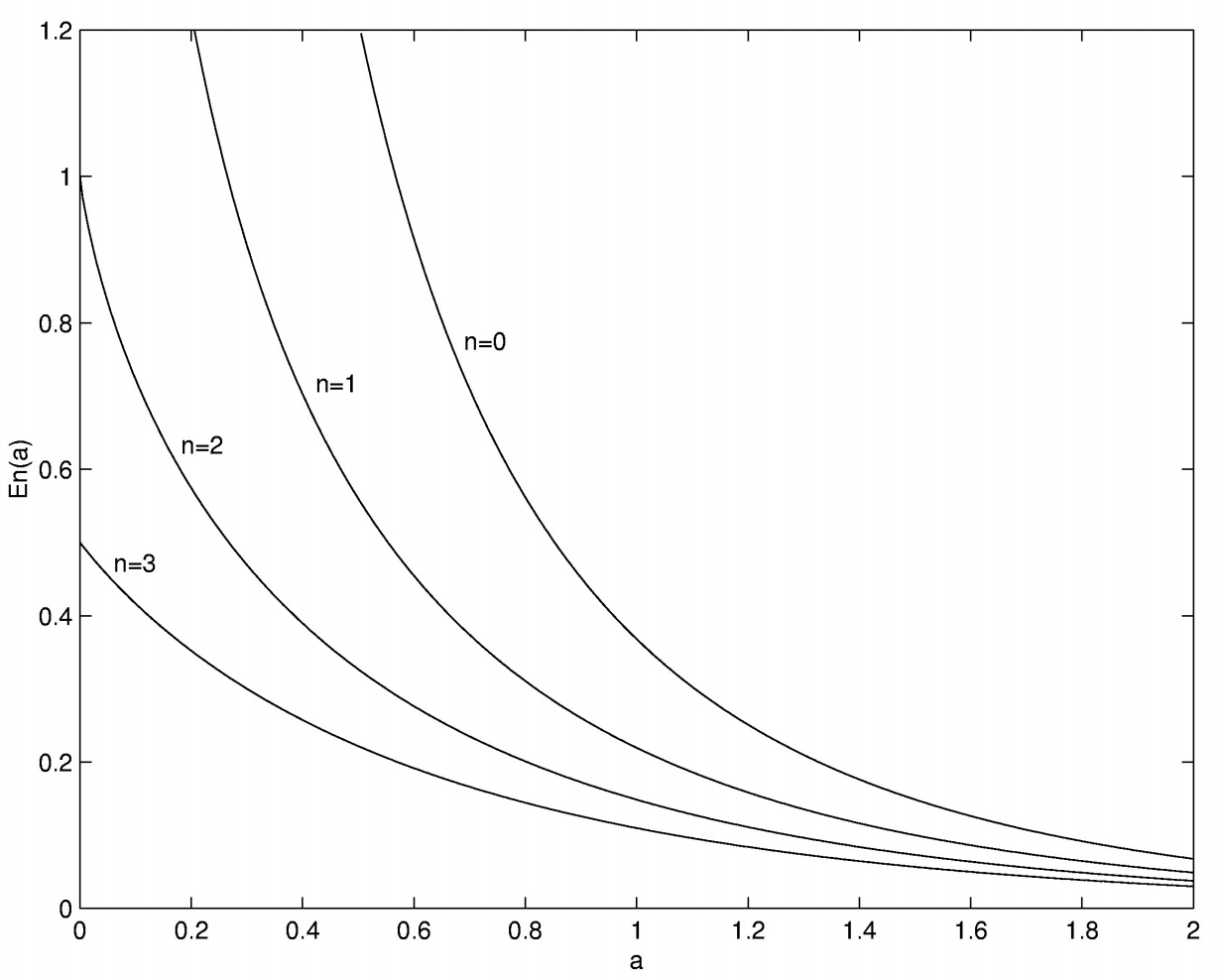
\(\text{FIGURE III.1}\)
La función integral exponencial