7.24: Reglas de selección

Se recordará que un multiplete es la totalidad de las transiciones entre dos términos. Por ejemplo,\(^3 \text{P} − \ ^3 \text{D}^\text{o}\) es el multiplete conectando los dos términos\(^3 \text{P}\) y\(^3 \text{D}^\text{o}\). Cada término tiene tres niveles, y por lo tanto hay nueve formas de conectar los niveles de un término con el otro, resultando cada transición en una línea. Pero de hecho sólo seis de estas transiciones están “permitidas” o “permitidas”, siendo las tres restantes “prohibidas”. Esto se debe a ciertas “reglas de selección”, o restricciones en la forma en que parte del número cuántico puede cambiar. De igual manera existen restricciones en el número de multipletes que pueden conectar los términos de dos poliadas, o sobre el número de componentes Zeeman que pueden conectar los estados de dos niveles. En todas estas situaciones existen reglas de selección que restringen que ciertos números cuánticos cambien en cantidades distintas a ciertas. En esta sección trataremos de entender de manera cualitativa cómo surgen tales reglas de selección. Vamos a enumerar las diversas reglas de selección, y ver cómo esto afectará el número de líneas en un multiplete, o el número de componentes en una línea.

Todo el mundo sabe que cuando un dipolo eléctrico oscila irradia una onda electromagnética. Del mismo modo, si un dipolo, en lugar de oscilar periódicamente, sufre repentinamente un cambio en su momento dipolar eléctrico − por ejemplo, si la distancia entre dos cargas eléctricas opuestas cambia repentinamente − se irradiará un pulso de radiación electromagnética. Si bien la radiación de un solo átomo se irradiará como la de un dipolo, en un gas con enormes números de átomos orientados en direcciones completamente aleatorias, la radiación aparecerá isotrópica.

Una manera razonable de explicar cómo un átomo irradia un pulso (un cuántico) de radiación electromagnética cuando cambia de un estado a otro es que su momento dipolo cambia, y la energía irradiada está relacionada con el cambio en su momento dipolar. De hecho, en la mecánica cuántica, la cantidad de energía que se irradia cuando un átomo cambia de un estado a otro viene determinada por el cuadrado de una cantidad conocida como momento de transición:

\[\int \psi_f^* \boldsymbol{\mu} \psi_i d \tau . \]

Aquí\(d\tau\) está el elemento de volumen habitual, y\(\psi_I\) es la ondafunción del estado inicial. \(\boldsymbol{\mu}\)es el operador del momento dipolo, que depende de las posiciones de todos los electrones en el átomo. \(\psi^*_f\)es el conjugado de la función de onda del estado final. Aquellos que tienen mucha práctica en la realización de tales cálculos tienen la experiencia suficiente para saber que el efecto del operador de momento dipolo es simplemente producir una función de onda similar con quizás algunos cambios en los números cuánticos. Por lo tanto, para guardar escribiendo la expresión completa para la función de onda en su totalidad, simplemente listan los números cuánticos de la función de onda inicial en un ket, y del conjugado de la función final en un sostén, así:

\[\langle L^\prime S^\prime J^\prime M^\prime | \boldsymbol{\mu} | LSJM \rangle . \]

Nuevamente, quienes hacen esos cálculos diariamente para ganarse la vida pronto reconocen, desde las simetrías mismas de las funciones de onda (teoría de grupos) y sin tener que preocuparse mucho por los detalles de las funciones, que este momento de transición es cero a menos que existan ciertas relaciones entre el cuántico inicial y el final números. Son esas transiciones las que resultan en un momento de transición distinto de cero las que están “permitidas”. Si el momento de transición es cero, que es a excepción de ciertas combinaciones de números cuánticos iniciales y finales, la transición está “prohibida”.

Por ejemplo, si estamos discutiendo los posibles componentes Zeeman de una línea, las únicas transiciones “permitidas” -es decir, los únicos momentos de transición distintos de cero- son aquellas en las que los valores inicial y final de\(M\) son iguales o difieren en\(\pm 1\). Decimos que la “regla de selección” para el efecto Zeeman es. \(\Delta M = 0, \ \pm 1\)Ya tomamos en cuenta esta restricción en el dibujo de las figuras VII.1 y VII.2. En el primero, en lugar de 15 componentes posibles, sólo hay nueve con momentos de transición distintos de cero y que satisfacen la regla de selección, y en la figura VII.2 sólo hay seis en lugar de ocho.

En realidad, al observar el efecto Zeeman, si vemos la luz desde una dirección perpendicular al campo magnético, vemos que los componentes con\(\Delta M = 0\) están polarizados planos paralelos al campo magnético, y se llaman los\(p\) -componentes, y los que\(\Delta M = \pm 1\) tienen son polarizados planos perpendicular al campo magnético, y se llaman los\(s\) -componentes (senkrecht alemán - perpendicular). (Puede parecer que los símbolos\(s\) y\(p\), sobre todo el primero, ya están haciendo más de lo que les corresponde en el trabajo). Si el espectro se ve desde una dirección a lo largo del campo magnético, se encontrará que\(s\) los -componentes están polarizados circularmente en sentidos opuestos, mientras que los\(p\) -componentes no son visibles en absoluto.

Así como el número de componentes Zeeman de una línea está limitado por la regla\(\Delta M = 0, \pm 1\) de selección de manera similar, el número de líneas posibles en un multiplete está limitado por una regla de selección\(\Delta J = 0, \pm 1\) (\(0 \leftrightarrow 0\)prohibida). Ya mencioné que un\(^3 \text{P} - \ ^3 \text{D}^\text{o}\) multiplete tiene apenas seis líneas en lugar de nueve. La Figura VII.3 muestra las posibles transiciones. (A diferencia de las figuras VII.1 y VII.2, en las que la escala horizontal era lineal en longitud de onda con longitud de onda aumentando hacia la derecha, la escala horizontal en la figura VII.3 no tiene significancia.)

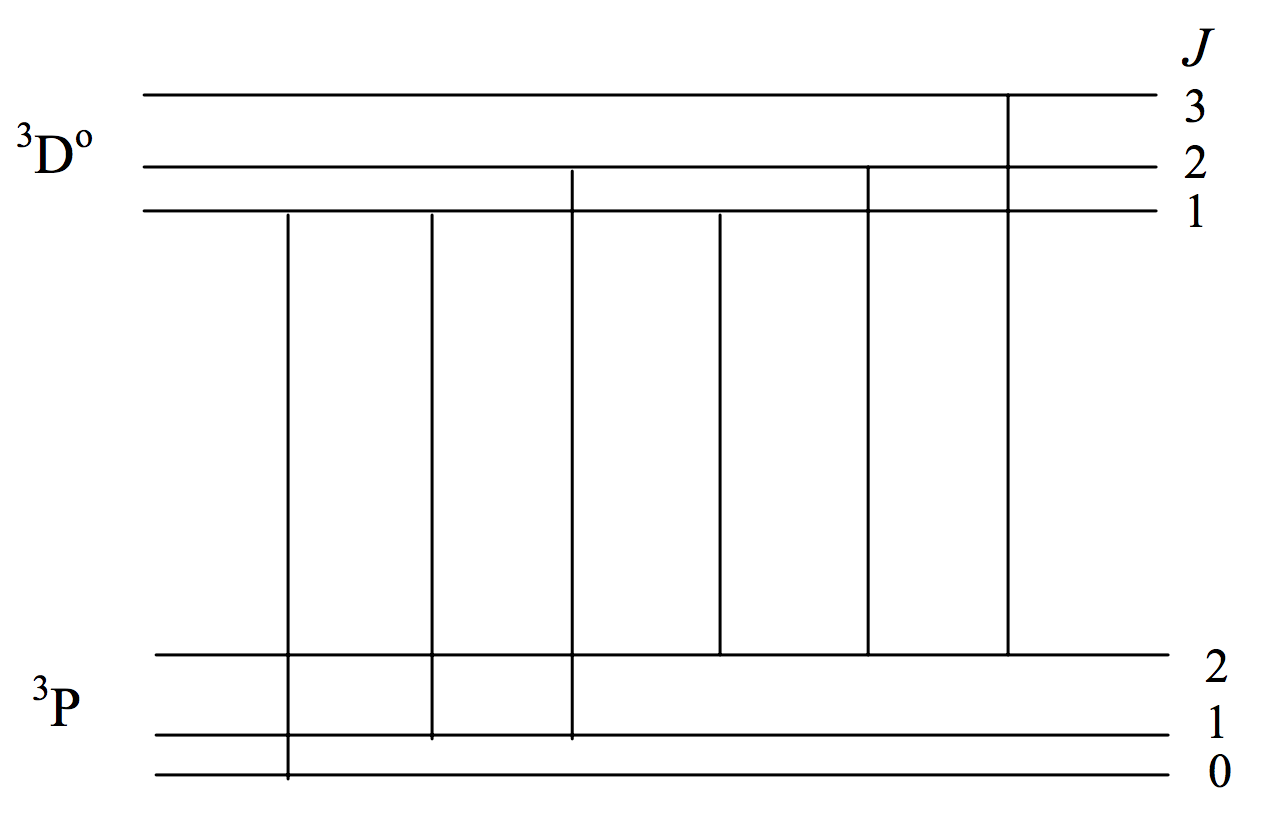
\(\text{FIGURE VII.3}\)

Puede ser que una línea, o un componente, esté prohibido dipolar la radiación y que, si µ es el operador eléctrico del momento dipolar, el momento de transición sea cero. Sin embargo, si sustituimos por el operador de momento dipolo al operador por cuadrupolo eléctrico o momento dipolo magnético, el momento de transición no es cero. En ese caso una transición que está prohibida a dipolo eléctrico (\(\text{E}1\)) radiación puede ser permitida a radiación eléctrica cuadrupolo (\(\text{E}2\)) o dipolo magnético (\(\text{M}1\)). \(\text{E}2\)y\(\text{M}1\) las transiciones son muy débiles y rara vez se observan en condiciones de laboratorio (aunque ocurren en fuentes astronómicas por razones que se explicarán más adelante). Por lo tanto, las líneas que están prohibidas a la radiación dipolar eléctrica generalmente se denominan simplemente líneas “prohibidas”, aunque en realidad no están prohibidas\(\text{E}2\) o\(\text{M}1\) radiación. El portador (átomo) de una línea prohibida a menudo se escribe entre paréntesis. Por ejemplo, hay una\(\text{E}2\) línea en el espectro de la aurora al\(557.7 \ \text{nm}\) surgir del átomo de oxígeno neutro, por lo que se dice que la línea es una línea de\([\text{O}_\text{ I}]\).

Algunos multipletes están prohibidos a la radiación dipolo eléctrico solo si los términos en cuestión se ajustan estrictamente a\(LS\) -acoplamiento, pero pueden ser permitidos para la radiación dipolo eléctrico si hay salidas de\(LS\) -acoplamiento. Tales transiciones son “semi-prohibidas”, y el portador a veces se escribe entre paréntesis y paréntesis. Por lo tanto hay una línea semi-prohibida en\(345.3 \ \text{nm}\) debido a\([\text{Al}_\text{ I})\). Para\(LS\) -acoplamiento, la radiación dipolo eléctrico está permitida solo si\(\Delta S = 0\). Es decir, se permiten transiciones entre dos términos de triplete, o entre dos términos singlete, pero no entre un triplete o un singlete. (En este sentido me refiero a un\(^3 \text{S}\) término como término “triplete”, a pesar de que sólo tiene un nivel). No todos usan esta convención entre corchetes y paréntesis.

En el átomo neutro de helio, hay términos singlete y triplete. \(LS\)-acoplamiento es la norma y, debido a esto, no hay transiciones entre ninguno de los términos singlete y un término triplete. De hecho, es como si hubiera dos conjuntos de términos completamente independientes y dos espectros, y de hecho los términos singlete y los términos triplete a veces se denominan “para-helio” y “orto-helio” respectivamente. En tales circunstancias es difícil (o imposible en ausencia de pruebas independientes adicionales) conocer las energías relativas de los términos triplete y singlete, o saber cuál es el término base del átomo − aunque ahora sabemos que el término suelo de helio es un\(^3 \text{S}\) término.

El calcio neutro también tiene un conjunto de términos singlete y un conjunto de términos triplete, pero hay salidas desde\(LS\) -acoplamiento, y hay multipletes que conectan singlete con términos triplete y viceversa. Dichos multipletes se denominan multipletes de “intercombinación” o “intersistema”. Por ejemplo, la línea at\(657.3 \ \text{nm}\) es miembro de un\(^1 \text{S} − \ ^3 \text{P}^\text{o}\) multiplete de\([\text{Ca}_\text{ I})\).

Aquí hay una lista de las diversas reglas de selección que se me ocurren. No he incluido el espín nuclear, pero se puede deducir cuáles son las reglas, dado que el acoplamiento entre el momento angular del electrón y el espín nuclear es generalmente puro\(JI\) -acoplamiento (análogo a\(LS\) -acoplamiento).

Para Transiciones Dipolares Eléctricas. Las transiciones tienen lugar entre términos de diferentes configuraciones, de tal manera que el\(l\) -valor de un electrón debe cambiar por\(\pm 1\). De ello se deduce que las transiciones permitidas están entre términos de paridad opuesta. Las líneas dentro de un multiplete están sujetas a la regla de selección\(\Delta J = 0, \ \pm 1\), excepto que\(0\) a\(0\) está prohibido. (Estas reglas se descomponen para la radiación dipolo eléctrico en presencia de un fuerte campo eléctrico externo, que no necesita preocuparnos aquí, sino que debe ser considerado con respecto al efecto Stark.) Los componentes Zeeman de una línea están sujetos a la regla de selección\(\delta M = 0, \pm 1\).

Para\(LS\) -acoplamiento, existen las siguientes restricciones adicionales. \(\Delta S = 0\); es decir, las transiciones intersistemas están prohibidas a la radiación dipolar eléctrica. Están “semi-prohibidos”. \(\Delta L = 0, \ \pm 1\), salvo que\(0\) a\(0\) esté prohibido. Así\(\text{S} − \ \text{S}^\text{o}\),\(\text{S} − \ \text{D}^\text{o}\), los\(\text{P} − \ \text{F}^\text{o}\) multipletes serían todos indicativos de salidas de\(LS\) -acoplamiento. Las transiciones también deben tener lugar entre términos de parentesco común.

Para Transiciones de Dipolo Magnético. Las transiciones tienen lugar entre términos de una sola configuración y, por lo tanto, entre términos de la misma paridad. Las líneas dentro de un multiplete están sujetas a la regla de selección\(\Delta J = 0, \ \pm 1\), excepto que\(0\) a\(0\) está prohibido. Los componentes Zeeman de una línea están sujetos a la regla de selección\(\Delta M = 0, \ \pm 1\), excepto eso\(\Delta J\) y\(\Delta M\) no pueden ser ambos cero.

Para\(LS\) -acoplamiento existen las restricciones adicionales\(\Delta S = 0\) y\(\Delta L = 0\).

Para Transiciones Cuatripolares Eléctricas. Las transiciones tienen lugar ya sea entre términos de la misma configuración o entre configuraciones en las que el\(l\) -valor de un electrón cambia por\(\pm 2\). En cualquier caso esto implica que las transiciones tienen lugar entre términos de una misma paridad. Las líneas dentro de un multiplete están sujetas a la regla de selección\(\Delta J = 0, \ \pm 1, \ \pm 2\), salvo eso\(0-0, \ \frac{1}{2}-\frac{1}{2}, \ 0-1\) y\(1-0\) están prohibidas. Esto implica que\(J^\prime + J^{\prime \prime}\) debe ser al menos\(2\). Los componentes Zeeman de una línea están sujetos a la regla de selección\(\Delta M = 0, \ \pm 1, \ \pm 2\).

Para\(LS\) -acoplamiento existen las restricciones adicionales\(\Delta S = 0\) y\(\Delta L = 0, \ \pm 1, \ \pm 2\), salvo que\(\Delta L = 0-0, \ 0-1, \ 1-0\) están prohibidas. Las transiciones también deben tener lugar entre términos de parentesco común.

Ejercicio. En la sección 7.16 enumeré los diez primeros niveles para el átomo de hidrógeno, es decir, los niveles en las tres primeras conchas. También aseveré que Hα comprende tres matrices de transición, tres multipletes, siete líneas y un número no especificado de componentes Zeeman. Ahora que estás familiarizado con las reglas de selección, estás en condiciones de verificar esto. Por lo tanto, como ejercicio, enumerar todos los arrays, multipletes y líneas que comprenden\(\text{H}\alpha\). (Debe asumir\(LS\) -acoplamiento; obviamente con un solo electrón no hay distinción entre\(LS\) - y\(jj\) -acoplamiento.) Por ejemplo,\(2p − 3d\) es una matriz. \(2p \ ^2\text{P}^\text{o} - 3d \ ^2\text{D}\)es un multiplete. \(2p \ ^2\text{P}_{\frac{3}{2}}^\text{o} - 3d \ ^2\text{D}_\frac{5}{2}\)es una línea. En la tabla de la sección 7.16, he enumerado el peso estadístico de cada nivel. Para cada nivel, enumere los\(M\) valores posibles, y luego, usando las reglas de selección de Zeeman, determine cuántos componentes Zeeman hay para cada nivel, y por lo tanto para\(H\alpha\) como un todo. ¿Cuántos de los componentes Zeeman tienen distintas longitudes de onda?

En el ejercicio anterior, quizá ignoró el efecto del giro nuclear. Ahora incluye giro nuclear (\(I = 1/2\)). Verás ahora que cada uno de los ocho niveles involucrados en la formación de\(\text{H}\alpha\) se divide en dos niveles hiperfinos con diferentes valores de\(F\). Ahora bien, ¿cuántos hiperfino y Zeeman hay?

Ahora contesta las mismas preguntas con deuterio. Se podría esperar que el núcleo de deuterio (el “deuterón”) tenga cero espín nuclear -pero no hay tal suerte, porque el giro del deuterón lo es\(I = 1\). Así, la mayoría de los niveles están compuestos por tres niveles hiperfinos. (¿Por qué dije “la mayoría”? Algunos de los niveles solo tienen dos niveles hiperfinos, ¿no? ¿Ves por qué?) ¿Cuántos componentes hiperfina y Zeeman están permitidos por las reglas de selección?

Por supuesto, el hidrógeno natural incluye ambos\(^1 \text{H}\) y una cantidad muy pequeña de\(^2 \text{H}\), y se exhibirán los espectros de ambos. ¡Verdaderamente\(\text{H}\alpha\) es una “línea” mucho más complicada de lo que imaginamos en la sección 7.3! Para agregar a la complicación, no debemos olvidar que bajo condiciones terrestres, el hidrógeno es molecular, y hay tres posibles isotopómeros\(\text{H}_2, \ \text{HD}\) -y\(\text{D}_2\) - y aquellos familiarizados con los espectros moleculares recordarán que existen diferencias obvias entre los espectros de homonuclear y moléculas heteronucleares. ¡Claramente, uno podría pasar toda la vida estudiando el espectro del hidrógeno!