9.1: Introducción, Resplandor y Ancho Equivalente

Si nos fijamos en un gas caliente y resplandeciente, podemos imaginar que podríamos medir su resplandor en\(\text{W m}^{-2}\text{ sr}^{-1}\). Si dispersamos la luz con un espectrógrafo, podemos ver que está compuesta por numerosas líneas de emisión discretas. Estas líneas no son infinitesimalmente estrechas, sino que tienen un ancho finito y un perfil medible. En cualquier longitud de onda particular dentro del intervalo de longitud de onda cubierto por la línea, supongamos que la luminosidad por intervalo de longitud de onda unitaria es\(I_λ\text{ W m}^{-2}\text{ sr}^{-1}\text{ m}^{-1}\). Aquí, estamos usando el símbolo\(I\) para resplandor, que es habitual en la astronomía, más que el símbolo\(L\), que usamos en el capítulo 1. Insistimos, sin embargo, en el uso correcto de la palabra “resplandor”, en lugar de la “intensidad” que a menudo se usa demasiado vagamente. Podríamos imaginar que podríamos medir\(I_λ\) comparando el intervalo de radiancia por unidad de longitud de onda en el espectro del gas con el intervalo de radiancia por unidad de longitud de onda de un cuerpo negro a una temperatura conocida (o de cualquier otro cuerpo cuya emisividad se conozca), observada en las mismas condiciones con el mismo espectrógrafo.

El resplandor\(I\) de toda la línea viene dada por\(I=\int_0^{\infty} I_λ\,dλ.\) En principio, los límites de integración son\(0\) y\(\infty\), aunque en la práctica para la mayoría de las líneas la integración necesita realizarse solo dentro de unas pocas décimas de un nanómetro desde el centro de la línea.

El resplandor de una línea de emisión depende, entre otras cosas, del número de átomos por unidad de área en la línea de visión (la “densidad de columna”) en el nivel inicial (es decir, superior) de la línea.

Habrás notado que escribí “depende de”, en lugar de “es proporcional a”. Podemos imaginar que el número de átomos por unidad de área en la línea de visión podría duplicarse ya sea duplicando la densidad (número de átomos por unidad de volumen), o duplicando la profundidad de la capa de gas. Si duplicar la densidad de la columna da como resultado una duplicación del resplandor de la línea, o, expresado de otra manera, si el resplandor de una línea es linealmente proporcional a la densidad de la columna, se dice que la línea es ópticamente delgada. Muy a menudo una línea no es ópticamente delgada, y el resplandor no es proporcional al número de átomos por unidad de área en el nivel superior. Volveremos a este tema en el capítulo sobre la curva de crecimiento. Mientras tanto, en este capítulo, a menos que se indique lo contrario, nos preocuparemos enteramente de fuentes ópticamente delgadas, en cuyo caso\(I \propto \mathcal{N}_2\), donde\(\mathcal{N}\) está la densidad de la columna y el subíndice denota el nivel superior. También supondremos que el gas es homogéneo y de una sola temperatura y presión uniformes en todas partes.

En materia de notación, estoy usando:

\[\nonumber\begin{align}n&=\text{number of atoms per unit volume} \\ \nonumber \mathcal{N}&=\text{column density}\\ \nonumber N&= \text{number of atoms} \\ \end{align}\]

Así en un volumen\(V,\, N = nV\), y en una capa de espesor\(t,\, \mathcal{N} = nt\).

La mayoría de las líneas en espectros estelares son líneas de absorción vistas contra un continuo más brillante. En una situación análoga de laboratorio, podemos imaginar una capa uniforme de gas vista contra un continuo. Supondremos que el intervalo de radiancia por unidad de longitud de onda de la fuente continua de fondo es\(I_λ(c)\). Estableceremos más notación haciendo referencia a la figura\(\text{IX.1}\), que representa una línea de absorción contra un continuo. El intervalo de radiancia por unidad de longitud de onda se traza contra la longitud de onda horizontalmente.

\(\text{FIGURE IX.1}\)

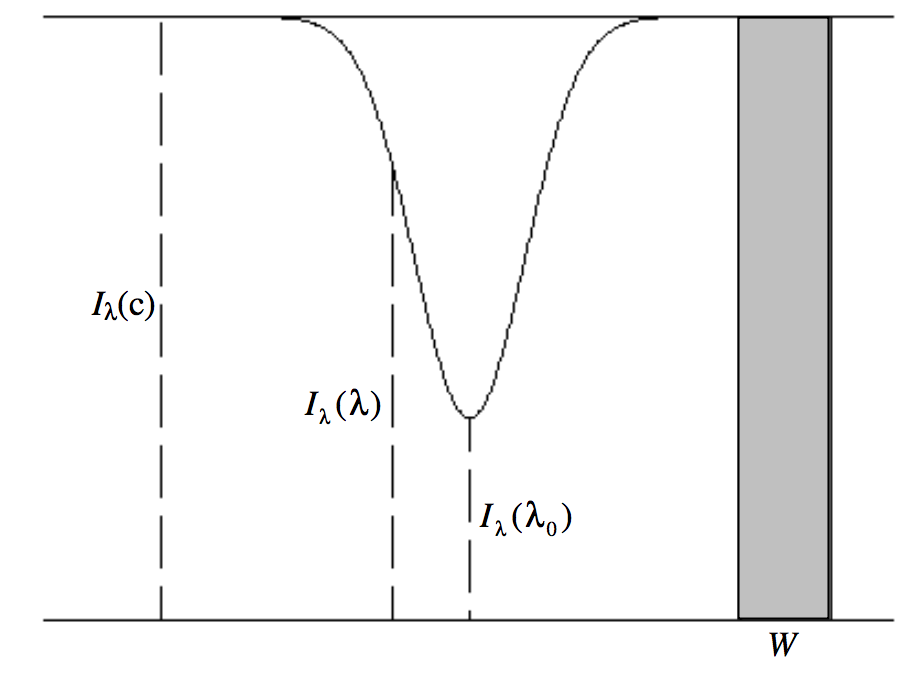
\(I_λ(λ)\)es el intervalo de radiancia por unidad de longitud de onda en alguna longitud de onda dentro del perfil de línea, y\(I_λ(λ_0)\) es la luminosidad por intervalo de longitud de onda unitaria en el centro de la línea.

El ancho equivalente\(W\) (\(\mathfrak{die\, Aequivalentbreite}\)) de una línea de absorción es el ancho del continuo adyacente que tiene la misma área que es ocupada por la línea de absorción. Expresado como una ecuación definitoria, esto significa:

\[WI_λ (c)=\int \left [ I_λ (c)-I_λ (λ )\right ]\,dλ.\label{9.1.1}\]

Nuevamente en principio los límites de integración son\(0\) a\(\infty\), aunque en la práctica bastarán unas décimas de nanómetro. El ancho equivalente se expresa en nm (o en Å). Debe destacarse que el ancho equivalente es una medida de la resistencia de una línea de absorción, y de ninguna manera está relacionado con el ancho real (o ancho completo a la mitad mínima) de la línea. En la figura\(\text{IX.1}\), el ancho\(W\) del continuo tiene la misma área que la línea de absorción.

En principio, el ancho equivalente también podría expresarse en unidades de frecuencia (Hz), a través de una ecuación definitoria:

\[W^{(\nu)}I_{\nu} (c) = \int \left [ I_{\nu} (c) -I_{\nu} (\nu) \right ] \,d\nu.\label{9.1.2}\]

Esto a veces se ve en discusiones teóricas, pero en la práctica el ancho equivalente suele expresarse en unidades de longitud de onda. Los dos están relacionados por

\[\label{9.1.3}W^{(\nu)}=\frac{c}{λ^2}W^{(λ)},\quad W^{(λ)}=\frac{c}{\nu^2}W^{(\nu)}.\]

A menos que se especifique lo contrario, omitiré el superíndice\((λ)\), y normalmente\(W\) significaré un ancho equivalente expresado en unidades de longitud de onda, como en la Ecuación\ ref {9.1.1}.

Ejercicio\(\PageIndex{1}\)

Una capa de gas frío se encuentra sobre una fuente extendida de radiación continua, y una línea de absorción formada en la capa de gas tiene un ancho equivalente\(W\). Si ahora se incrementa la temperatura de la fuente continua extendida para que se duplique su resplandor espectral a la longitud de onda de la línea, ¿cuál será ahora el ancho equivalente de la línea?

El ancho equivalente de una línea de absorción depende, entre otras cosas, del número de átomos por unidad de área en la línea de visión (la “densidad de columna”) en el nivel inicial (es decir, inferior) de la línea. Si el gas es ópticamente delgado\(W \propto \mathcal{N}_1\),, donde el subíndice indica el nivel inferior de la línea.

Si el coeficiente de absorción a longitud de onda\(λ\text{ is }\alpha (λ)\) y tiene el mismo valor en todo el gas, y el espesor de la capa de gas\(t,\, I_λ(λ)\text{ and }I_λ(c)\) se relacionan por

\[\label{9.1.4}I_λ (λ) =I_λ (c)\text{exp}\left [ -\alpha (λ)t\right ].\]

Así se puede escribir la ecuación\ ref {9.1.1}

\[\label{9.1.5}W=\int \left [1-\text{exp}\left ( -\alpha (λ)t\right ) \right ] \,dλ ,\]

y esta ecuación a veces se cita como la definición del ancho equivalente. La definición, sin embargo, es la Ecuación\ ref {9.1.1}. La ecuación\ ref {9.1.4} se puede usar para calcularlo, pero solo si\(\alpha (λ)\) es uniforme en todo el gas. En el límite ópticamente delgado, el primer término en la expansión Maclaurin de\(1- \text{exp}\left (- \alpha (λ)t\right )\text{ is }\alpha (λ)t\), de manera que, para un gas homogéneo ópticamente delgado,

\[\label{9.1.6}W=t\int \alpha (λ)dλ.\]

El lector debe verificar, como siempre, la corrección dimensional de todas las ecuaciones anteriores.

Hemos visto que el resplandor de una línea de emisión o el ancho equivalente de una línea de absorción depende, entre otras cosas, de la densidad de la columna de átomos en el estado inicial. De hecho, en un gas homogéneo ópticamente delgado, la luminosidad o anchura equivalente es linealmente proporcional al producto de dos cosas. Una es la densidad de la columna de átomos en el estado inicial. El otro es una propiedad intrínseca del átomo, o más bien de los dos niveles atómicos involucrados en la formación de la línea, que determina cuánta energía emite o absorbe un solo átomo. Hay tres cantidades comúnmente utilizadas para describir esta propiedad, a saber, la fuerza del oscilador, el coeficiente de Einstein y la intensidad de la línea.

Estas tres cantidades están relacionadas por ecuaciones simples, pero la fuerza del oscilador es particularmente apropiada cuando se discuten las líneas de absorción, el coeficiente de Einstein es particularmente apropiado cuando se discuten las líneas de emisión, mientras que la intensidad de la línea es un cuántico cantidad mecánica particularmente útil en el trabajo teórico. Debido a este uso muy técnico del término fuerza de línea, el término no debe usarse simplemente para describir cuán “intensa” parece ser una línea en particular.