10.6: Ampliamiento Rotacional

Las líneas en el espectro de una estrella giratoria se ensanchan debido a que la luz de la extremidad que retrocede se desplaza al rojo y la luz de la extremidad que se aproxima es desplazada al azul. Se puede observar que las estrellas de tipo temprano (tipo F y anteriores) tienden a ser rotadoras mucho más rápidas que las estrellas de tipo posterior y, en consecuencia, las estrellas de tipo temprano muestran más ensanchamiento rotacional. También se debe remarcar que los rotadores pole-on no muestran, por supuesto, ensanchamiento rotacional (incluso rotadores rápidos de tipo temprano).

Me apegaré a la costumbre astronómica y me referiré a un “desplazamiento al rojo” como un desplazamiento hacia una longitud de onda más larga, ¡aunque para una línea infrarroja un “desplazamiento al rojo” en este sentido sería un desplazamiento lejos del rojo! Un turno “largo” tampoco resuelve el problema del todo, por la siguiente razón. Si bien es cierto que la relatividad no hace distinción entre una fuente móvil y un observador en movimiento, en el caso del efecto Doppler en el contexto del sonido en el aire, si el observador se mueve, puede haber un cambio en el tono del sonido percibido, ¡pero no hay cambio en la longitud de onda!

Comenzaremos considerando una estrella cuyo eje de rotación esté en el plano del cielo, y que sea de resplandor uniforme a través de su superficie. Luego pasaremos a los rotadores oblicuos, y luego a las estrellas oscurecidas en las extremidades. Otra complicación que podría considerarse sería la rotación no uniforme. Así, el Sol no gira como un cuerpo sólido, sino que la velocidad angular a latitudes bajas es más rápida que a latitudes más altas —la llamada “aceleración ecuatorial”.

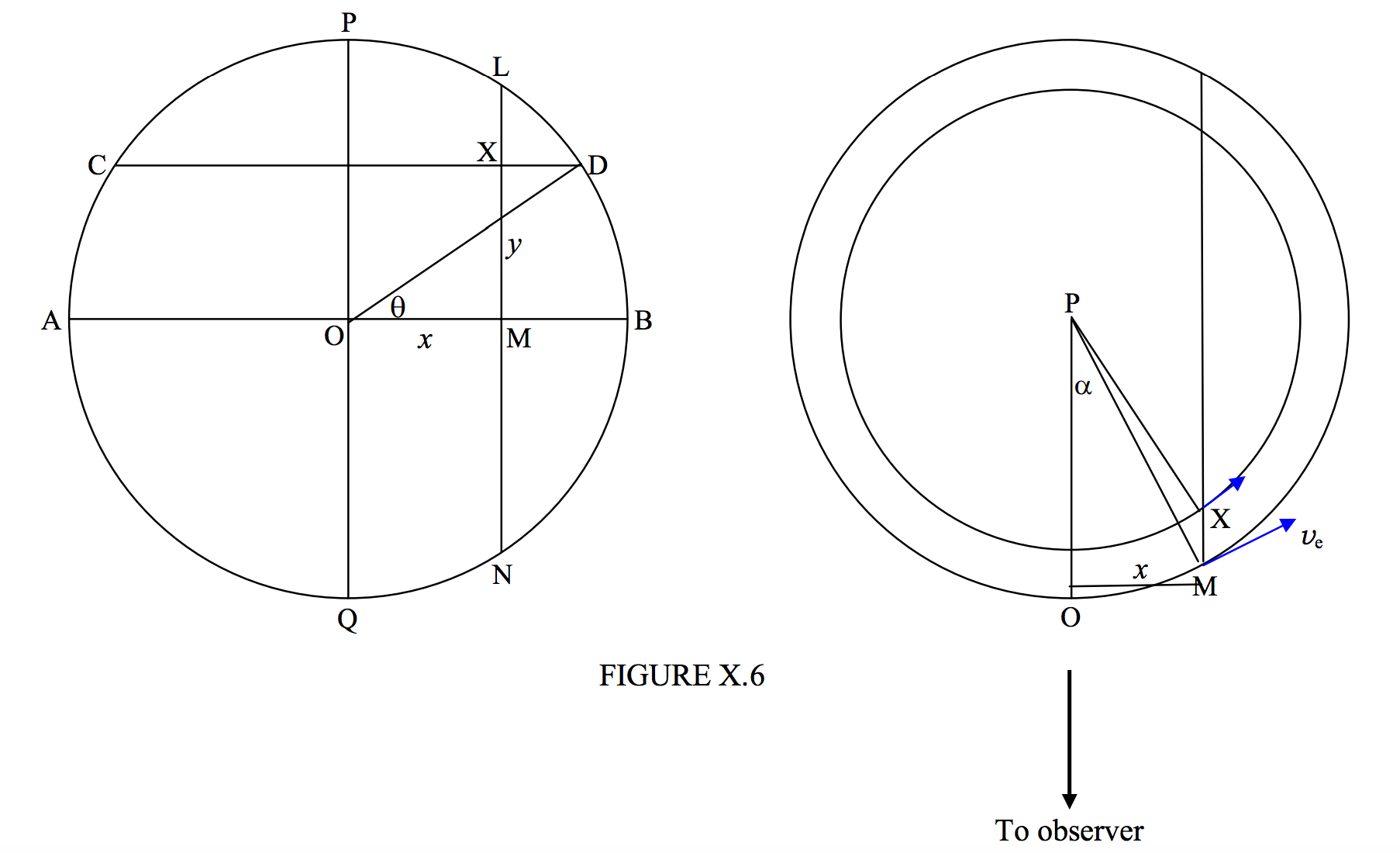
En la figura X.6, en la mano izquierda vemos el disco de una estrella tal como lo ve en el cielo un observador. PQ es el eje de rotación, se supone que está en el plano del cielo, y AB es el ecuador. X es un punto en la superficie de la estrella en coordenadas\((x, y)\), latitud\(\theta\). Se supone que la estrella está rotando con una velocidad ecuatorial\(v_e\). Lo que vamos a mostrar es que todos los puntos de la cuerda LMN tienen la misma velocidad radial lejos o hacia el observador, y en consecuencia toda la luz de los puntos de esta cuerda tiene el mismo desplazamiento Doppler.

La parte derecha de la figura muestra la estrella vista desde arriba del polo P. El pequeño círculo es el paralelo de latitud CD que se muestra en la parte izquierda de la figura.

M es un punto en el ecuador y también en el acorde LMN. Su velocidad es\(v_e\) y la componente radial de su velocidad es\(v_e \sin \alpha\). La velocidad del punto M es\(v_e \cos \theta\), y su velocidad radial es\(v_e \cos \theta \sin \text{OPX}\). Pero\(x = \text{PM} \sin \alpha = a \sin \alpha\text{ and }x = \text{PX} \sin \text{OPX} = a \cos \theta \sin \text{OPX}\). Por lo tanto\(\cos \theta \sin \text{OPX} = \sin \alpha\). Por lo tanto la velocidad radial de X es\(v_e \sin \alpha\), que es la misma que la de M, y por lo tanto todos los puntos en la cuerda LMN tienen velocidad radial\(v_e \sin \alpha = v_e x/a\).

Por lo tanto, todos los puntos de la\(x =\) constante de cuerda están sujetos al mismo desplazamiento Doppler

\[\label{10.7.1}\dfrac{\Delta \lambda}{\lambda}=\dfrac{v_e x}{ac}.\]

La ordenada de un perfil de línea de emisión en cambio Doppler en\(\Delta \lambda\) comparación con su ordenada en el centro de la línea es igual a la relación entre la longitud de la\(x =\) constante de cuerda y el diámetro\(2a\) del disco estelar:

\[\label{10.7.2}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=\left ( 1-\frac{x^2}{a^2}\right )^{\frac{1}{2}}=\left ( 1-\frac{c^2\left (\Delta \lambda \right )^2 }{v_e^2\lambda^2}\right )^\frac{1}{2}.\]

En lo anterior, hemos asumido que el eje de rotación está en el plano del cielo, o que la inclinación\(i\) del ecuador con respecto al plano del cielo está\(90^\circ\). Si la inclinación no lo es\(90^\circ\), el único efecto es que todas las velocidades radiales se reducen en un factor de\(\sin i\), de manera que la Ecuación\ ref {10.7.2} se convierte

\[\label{10.7.3}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=\left ( 1-\frac{c^2\left ( \Delta \lambda \right )^2}{v_e^2 \sin^2 i \lambda^2}\right )^\frac{1}{2},\]

y este es el perfil de línea. Es una elipse, y si escribimos\(\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=X \text{ and }\frac{\Delta \lambda}{\lambda}=Y\) Ecuación\ ref {10.7.3} se puede escribir

\[\label{10.7.4}\frac{x^2}{\left ( \frac{v_e \sin i}{c}\right )^2}+\frac{y^2}{1^2}=1.\]

El ancho basal de la línea (que no tiene alas asintóticas) es\(\frac{2v_e \sin i}{c}\) y el FWHM es\(\frac{\sqrt{3}v_e\sin i}{c}\). El perfil de una línea de absorción de profundidad central\(d\) es

\[\label{10.7.5}\frac{I_\lambda \left ( \Delta \lambda \right )}{I_\lambda (0)}=1-d\left (1-\frac{c^2 \left (\Delta \lambda \right )^2}{v_e^2\sin^2 i\lambda^2}\right )^\frac{1}{2},\]

Se deja como ejercicio para demostrar que

\[\text{Equivalent width}=\frac{\pi}{\sqrt{12}}\times \text{central depth}\times \text{FWHm}=0.9069 dw .\label{10.7.6}\]

A partir del ancho de una línea rotacionalmente ensanchada podemos determinar\(v_e \sin i\), pero no podemos determinar\(v_e\text{ and }i\) por separado sin información adicional. De igual manera, no podemos determinar la velocidad angular de rotación a menos que sepamos el radio de manera independiente.

Cabe señalar que, para un planeta giratorio, visible solo por la luz reflejada, el efecto Doppler se duplica por la reflexión, por lo que el ancho basal de una línea rotacionalmente ensanchada es

\[\dfrac{4v_e \sin i}{c}. \nonumber\]

Ahora examinemos el efecto del oscurecimiento de las extremidades. Voy a usar las palabras intensidad y resplandor en sus sentidos estrictamente correctos como se describe en el Capítulo 1, y los símbolos\(I\text{ and }L\) respectivamente. Es decir, resplandor = intensidad por unidad de área proyectada. Para la intensidad espectral y la radiancia espectral, es decir, intensidad y luminosidad por unidad de intervalo de longitud de onda, utilizaré un subíndice\(\lambda\).

\(\text{FIGURE X.7}\)

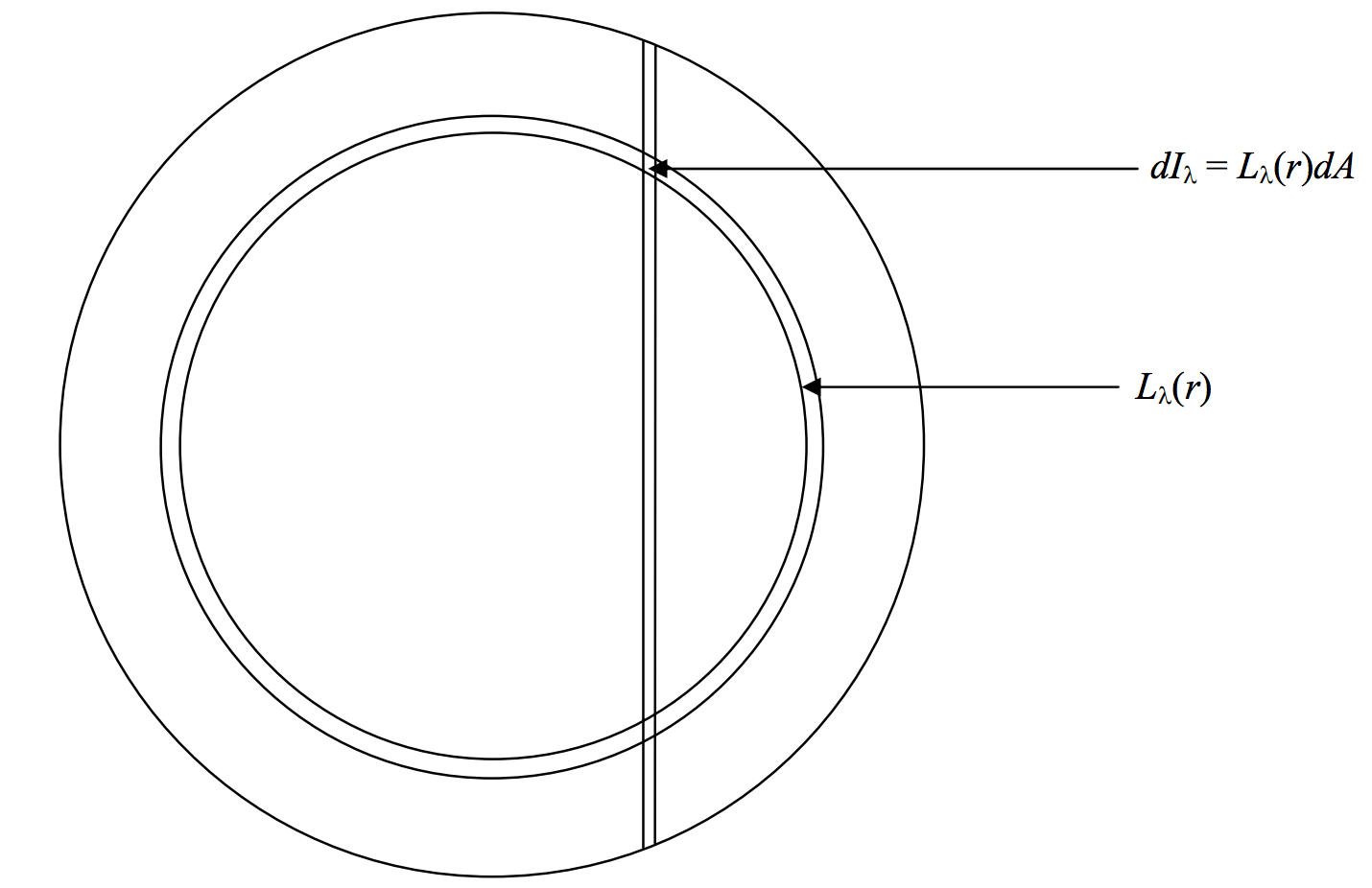
Suponemos que el resplandor espectral a una\(r\) distancia del centro del disco es\(L_\lambda (r)\). La intensidad de un área elemental\(dA\) en el disco es\(dI_\lambda = L_\lambda (r)dA\). El área entre la franja vertical y el anillo en la figura X.7 es un pequeño paralelogramo de largo\(dy\) y ancho\(dx\), de manera que eso\(dA = dxdy\). Aquí\(y^2 = r^2 - x^2\), para que

\[dy=\frac{rdr}{y}=\dfrac{rdr}{\sqrt{r^2-x^2}}. \nonumber\]

Por lo tanto\(dA=\frac{rdrdx}{\sqrt{r^2-x^2}}\). La intensidad total de la franja de ancho\(dx\), que es\(dI_\lambda (\Delta \lambda)\), donde\(\frac{\Delta \lambda}{\lambda}=\frac{xv_e \sin i}{ac}\), es

\[\label{10.7.7}dI_\lambda (\Delta \lambda) = 2\int_x^a \dfrac{L_\lambda (r)rdr}{\sqrt{r^2-x^2}}dx.\]

El perfil de línea (emisión) es

\[\label{10.7.8}\frac{I_\lambda (\Delta \lambda)}{I_\lambda (0)}=\dfrac{\int_x^a \frac{L_\lambda (r)rdr}{\sqrt{r^2-x^2}}dx}{\int_0^a L_\lambda (r)dr},\]

que es el perfil de la línea. Como ejercicio, vea si puede encontrar una expresión para el perfil de línea si el limb=oscurecimiento viene dado por\(L_\theta =L(0)[1-u(1-\cos \theta)]\), y mostrar que si el coeficiente de oscurecimiento de la extremidad\(u = 1\), el perfil es parabólico.

La ecuación\ ref {10.7.8} le permite calcular el perfil de línea, dado el oscurecimiento de la extremidad. El problema más práctico, pero más difícil, es invertir la Ecuación y, a partir del perfil de línea observado, encontrar el oscurecimiento de la extremidad. Ejemplos de esta integral, y su inversión por solución de una ecuación integral, son dados por Tatum y Jaworski, J. Quant. Espectr. Rad. Traslado, 38, 319, (1987).

Otra búsqueda de este problema sería calcular el perfil de línea de una estrella uniforme que está girando más rápido en el ecuador que en los polos, y luego para una estrella que esté a la vez oscurecida y acelerada ecuatorialmente, y luego ver si es posible invertir el problema de manera única y determinar tanto la extremidad oscurecimiento y aceleración ecuatorial a partir del perfil de línea. Eso sería todo un reto.