24.3: Pruebas de Relatividad General

Objetivos de aprendizaje

Al final de esta sección, podrás:

• Describir el movimiento inusual de Mercurio alrededor del Sol y explicar cómo la relatividad general explica el comportamiento observado
• Proporcionar ejemplos de evidencia de que los rayos de luz son doblados por objetos masivos, como lo predice la teoría de la relatividad general sobre la deformación del espacio-tiempo

Lo que Einstein propuso fue nada menos que una gran revolución en nuestra comprensión del espacio y el tiempo. Era una nueva teoría de la gravedad, en la que la masa determina la curvatura del espacio-tiempo y esa curvatura, a su vez, controla cómo se mueven los objetos. Como todas las nuevas ideas en la ciencia, sin importar quién las avance, la teoría de Einstein tuvo que ser probada comparando sus predicciones con la evidencia experimental. Esto fue todo un reto porque los efectos de la nueva teoría eran evidentes sólo cuando la masa era bastante grande. (Para masas más pequeñas, requería técnicas de medición que no estarían disponibles hasta décadas después).

Cuando la masa distorsionadora es pequeña, las predicciones de la relatividad general deben estar de acuerdo con las resultantes de la ley de la gravitación universal de Newton, que, después de todo, nos ha servido admirablemente en nuestra tecnología y en guiar sondas espaciales a los otros planetas. En territorio familiar, por lo tanto, las diferencias entre las predicciones de los dos modelos son sutiles y difíciles de detectar. Sin embargo, Einstein pudo demostrar una prueba de su teoría que se podía encontrar en los datos existentes y sugerir otra que se probaría pocos años después.

El movimiento de Mercurio

De los planetas de nuestro sistema solar, Mercurio orbita más cerca del Sol y es así más afectado por la distorsión del espacio-tiempo producida por la masa del Sol. Einstein se preguntó si la distorsión podría producir una diferencia notable en el movimiento de Mercurio que no fue predicha por la ley de Newton. Resultó que la diferencia era sutil, pero definitivamente estaba ahí. Lo más importante es que ya se había medido.

Mercurio tiene una órbita altamente elíptica, de modo que solo está a unos dos tercios de distancia del Sol en el perihelio como en el afelio (estos términos se definieron en el capítulo sobre Órbitas y Gravedad). Los efectos gravitacionales (perturbaciones) de los otros planetas sobre Mercurio producen un avance calculable del perihelio de Mercurio. Lo que esto significa es que cada perihelio sucesivo ocurre en una dirección ligeramente diferente como se ve desde el Sol (Figura\(\PageIndex{1}\)).

Figura El bamboleo de\(\PageIndex{1}\) Mercurio. El eje mayor de la órbita de un planeta, como Mercurio, gira ligeramente en el espacio debido a diversas perturbaciones. En el caso de Mercurio, la cantidad de rotación (o precesión orbital) es un poco mayor de lo que pueden explicar las fuerzas gravitacionales ejercidas por otros planetas; esta diferencia se explica precisamente por la teoría general de la relatividad. Mercurio, siendo el planeta más cercano al Sol, tiene su órbita más afectada por la deformación del espacio-tiempo cerca del Sol. El cambio de órbita a órbita se ha exagerado significativamente en este diagrama.

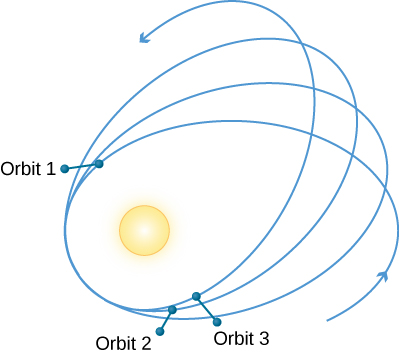
Según la gravitación newtoniana, las fuerzas gravitacionales ejercidas por los planetas harán que el perihelio de Mercurio avance unos 531 segundos de arco (arcsec) por siglo. En el siglo XIX, sin embargo, se observó que el avance real es de 574 arcsec por siglo. La discrepancia fue señalada por primera vez en 1859 por Urbain Le Verrier, el codescubridor de Neptuno. Así como las discrepancias en el movimiento de Urano permitieron a los astrónomos descubrir la presencia de Neptuno, así se pensó que la discrepancia en el movimiento de Mercurio podría significar la presencia de un planeta interior por descubrir. Los astrónomos buscaron este planeta cerca del Sol, incluso dándole un nombre: Vulcano, después del dios romano del fuego. (El nombre sería usado posteriormente para el planeta natal de un personaje famoso en un popular programa de televisión sobre futuros viajes espaciales).

Pero nunca se ha encontrado ningún planeta más cerca del Sol que Mercurio, y la discrepancia seguía molestando a los astrónomos cuando Einstein estaba haciendo sus cálculos. La relatividad general, sin embargo, predice que debido a la curvatura del espacio-tiempo alrededor del Sol, el perihelio de Mercurio debería avanzar ligeramente más de lo que predice la gravedad newtoniana. El resultado es hacer que el eje mayor de la órbita de Mercurio gire lentamente en el espacio debido solo a la gravedad del Sol. La predicción de la relatividad general es que la dirección del perihelio debería cambiar 43 segundos adicionales por siglo. Esto se acerca notablemente a la discrepancia observada, y le dio mucha confianza a Einstein a medida que avanzaba en su teoría. El avance relativista del perihelio se observó posteriormente también en las órbitas de varios asteroides que se acercan al Sol.

Desviación de Starlight

La segunda prueba de Einstein fue algo que no se había observado antes y que así proporcionaría una excelente confirmación de su teoría. Dado que el espacio-tiempo es más curvo en regiones donde el campo gravitacional es fuerte, esperaríamos que la luz que pasa muy cerca del Sol pareciera seguir un camino curvo (Figura\(\PageIndex{2}\)), al igual que el de la hormiga en nuestra analogía. Einstein calculó a partir de la teoría de la relatividad general que la luz de las estrellas que solo pastoreaba la superficie del Sol debería desviarse en un ángulo de 1.75 segundos de arco. ¿Podría observarse tal desviación?

Figura\(\PageIndex{2}\) Curvatura de Senderos de Luz cerca del Sol.La luz de las estrellas que pasa cerca del Sol es desviada ligeramente por la “deformación” del espacio-tiempo. (Esta desviación de la luz estelar es un pequeño ejemplo de un fenómeno llamado lente gravitacional, que discutiremos con más detalle en La evolución y distribución de las galaxias). Antes de pasar por el Sol, la luz de la estrella viajaba paralela al borde inferior de la figura. Al pasar cerca del Sol, el camino se alteró ligeramente. Cuando vemos la luz, asumimos que el haz de luz ha estado viajando en un camino recto a lo largo de su recorrido, y así medimos la posición de la estrella para que sea ligeramente diferente de su verdadera posición. Si tuviéramos que observar la estrella en otro momento, cuando el Sol no está en el camino, mediríamos su verdadera posición.

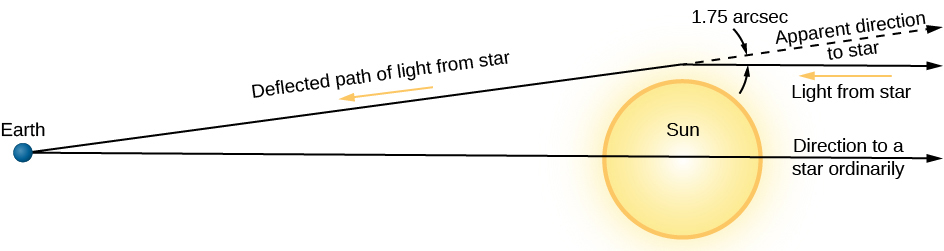
Nos encontramos con un pequeño “problema técnico” cuando tratamos de fotografiar la luz de las estrellas que se acerca mucho al Sol: el Sol es una fuente escandalosamente brillante de luz estelar en sí misma. Pero durante un eclipse solar total, gran parte de la luz del Sol queda bloqueada, permitiendo que las estrellas cercanas al Sol sean fotografiadas. En un artículo publicado durante la Primera Guerra Mundial, Einstein (escrito en una revista alemana) sugirió que las observaciones fotográficas durante un eclipse podrían revelar la desviación de la luz que pasa cerca del Sol.

La técnica consiste en tomar una fotografía de las estrellas seis meses antes del eclipse y medir la posición de todas las estrellas con precisión. Después las mismas estrellas son fotografiadas durante el eclipse. Aquí es cuando la luz de las estrellas tiene que viajar a nosotros bordeando el Sol y moviéndose a través del espacio-tiempo mensurablemente deformado. Como se ve desde la Tierra, las estrellas más cercanas al Sol parecerán estar “fuera de lugar” —ligeramente alejadas de sus posiciones regulares según se mide cuando el Sol no está cerca.

Un solo ejemplar de ese papel, pasado por la Holanda neutra, llegó al astrónomo británico Arthur S. Eddington, quien señaló que el siguiente eclipse adecuado fue el 29 de mayo de 1919. Los británicos organizaron dos expediciones para observarlo: una en la isla de Príncipe, frente a la costa de África occidental, y otra en Sobral, en el norte de Brasil. A pesar de algunos problemas con el clima, ambas expediciones obtuvieron fotografías exitosas. Las estrellas vistas cerca del Sol fueron efectivamente desplazadas, y a la precisión de las mediciones, que fue de alrededor del 20%, los cambios fueron consistentes con las predicciones de relatividad general. Experimentos más modernos con ondas de radio que viajan cerca del Sol han confirmado que los desplazamientos reales están dentro del 1% de lo que predice la relatividad general.

La confirmación de la teoría por las expediciones del eclipse en 1919 fue un triunfo que convirtió a Einstein en una celebridad mundial.

Resumen

En campos gravitacionales débiles, las predicciones de la relatividad general concuerdan con las predicciones de la ley de la gravedad de Newton. Sin embargo, en la gravedad más fuerte del Sol, la relatividad general hace predicciones que difieren de la física newtoniana y pueden ser probadas. Por ejemplo, la relatividad general predice que las ondas de luz o de radio serán desviadas cuando pasen cerca del Sol, y que la posición donde se encuentra Mercurio en el perihelio cambiaría 43 segundos de arco por siglo aunque no hubiera otros planetas en el sistema solar que perturbaran su órbita. Estas predicciones han sido verificadas por observación.