2.4: La hipérbola

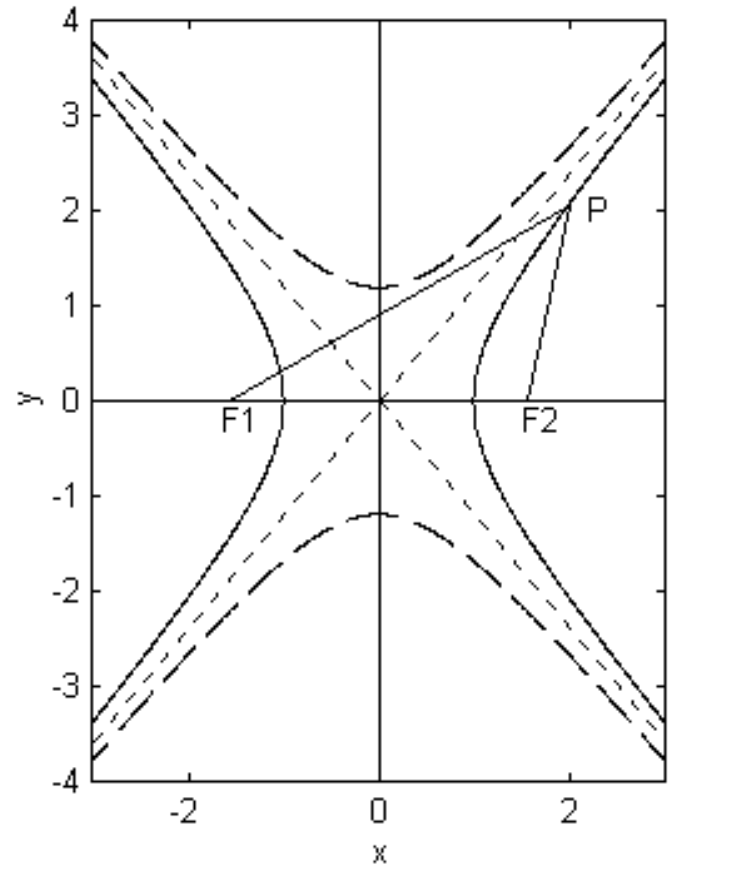
Una hipérbola es el locus de un punto que se mueve de tal manera que la diferencia entre sus distancias desde dos puntos fijos llamados focos es constante. Llamaremos a la diferencia entre estas dos distancias\(2a\) y la distancia entre los focos\(2ae\), donde\(e\) está la excentricidad de la hipérbola, y es un número mayor que 1. Ver figura\(\text{II.28}\).

\(\text{FIGURE II.28}\)

Por ejemplo, en un experimento de interferencia de doble hendidura de Young,\(m\) la franja brillante se ubica en un punto de la pantalla de tal manera que la diferencia de trayectoria para los rayos de las dos hendiduras son\(m\) las longitudes de onda. A medida que la pantalla se mueve hacia adelante o hacia atrás, esta relación continúa manteniéndose para la franja brillante\(m\) th, cuyo locus entre las hendiduras y la pantalla es, por lo tanto, una hipérbola. El sistema de navegación por radar “Decca”, utilizado por primera vez en los aterrizajes del Día D en la Segunda Guerra Mundial y dado de baja tan solo hasta el año 2000 por haber quedado obsoleto por el sistema “GPS” (Global Positioning Satellite), dependía de esta propiedad de la hipérbola. (Desde que se redactó esto, parte del sistema Decca se ha vuelto a poner en marcha como respaldo en caso de problemas con el GPS). Dos transmisores de radar a cierta distancia transmitirían simultáneamente pulsos de radar. Un barco recibiría las dos señales separadas por un corto intervalo de tiempo, dependiendo de la diferencia entre las distancias desde la nave hasta los dos transmisores. Esto colocó a la nave sobre una hipérbola en particular. El barco también escucharía otro par de transmisores, y esto colocaría al barco en una segunda hipérbola. Esto colocó entonces la nave en uno de los cuatro puntos donde se cruzaban las dos hipérbolas. Normalmente sería obvio cuál de los cuatro puntos era el correcto, pero cualquier ambigüedad podría resolverse por las señales de un tercer par de transmisores.

En la figura\(\text{II.28}\), las coordenadas de\(F_1\) y\(F_2\) son, respectivamente,\((−ae , 0)\) y\((ae , 0)\).

La condición\(\text{PF}_1 − \text{PF}_2 = 2a\) requiere que

\[\left[ (x + ae)^2 + y^2 \right]^{\dfrac{1}{2}} - \left[ (x-ae)^2 + y^2 \right]^{\dfrac{1}{2}} = 2a, \label{2.5.1} \tag{2.5.1}\]

y esta es la Ecuación a la hipérbola. Después de algún arreglo, esto se puede escribir

\[\dfrac{x^2}{a^2} - \dfrac{y^2}{a^2 (e^2 -1)} = 1, \label{2.5.2} \tag{2.5.2}\]

que es una forma más familiar para la Ecuación a la hipérbola. Definamos una longitud\(b\) por

\[b^2 = a^2 (e^2 - 1). \label{2.5.3} \tag{2.5.3}\]

La Ecuación se convierte entonces

\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1, \label{2.5.4} \tag{2.5.4}\]

que es la forma más familiar para la Ecuación a una hipérbola.

Ejemplo 1

Cuando un meteorito cruza el cielo, puede ser rastreado por radar. La instrumentación de radar puede determinar el alcance (distancia) del meteoroide en función del tiempo. Demostrar que, si el meteoroide se mueve a velocidad constante (una suposición cuestionable, porque debe estar desacelerando, pero quizás podamos suponer que la disminución de velocidad es insignificante durante el transcurso de la observación), y si el rango\(r\) se traza contra el tiempo, la gráfica será una hipérbola. Mostrar también que, si\(r^2\) se traza en contra\(t\), la gráfica será una parábola de la forma

\[r^2 = a t^2 + bt + c, \]

donde\(a=V^2 , \ b = -2V^2 t_0, \ c = V^2 t_0^2 + r_0^2, \ V = \text{speed of the meteoroid}, \ t_0 = \text{time of closest approach}, \ r_0 = \text{distance of closest approach}\).

La observación por radar de un meteoro arroja los siguientes datos de rango de tiempo:

\ begin {array} {c l}
t (\ text {s}) & r (\ text {km})\
\\
0.0 & 101.4\ *\
0.1 & 103.0\\
0.2 & 105.8\\
0.3 & 107.8\\
0.4 & 111.1\\
0.5 & 112.6\\
0.6 & amperio; 116.7\\
0.7 & 119.3\\
0.8 & 123.8\ *\
0.9 & 126.4\\
1.0 & 130.6\\
1.1 & 133.3\\
1.2 & 138.1\\
1.3 & 141.3\ *\
\ end {array}

Supongamos que la velocidad del meteoro es constante.

Determinar i. El tiempo de aproximación más cercano (a 0.01\(\text{s}\))
ii. La distancia de aproximación más cercana (a 0.1\(\text{km}\))
iii. La velocidad (a 1.0\(\text{km s}^{-1}\))

Si lo desea, sólo tiene que utilizar los tres datos con asteriscos para determinar\(a\),\(b\) y\(c\). Si eres más enérgico, usa todos los datos, y determina\(a\),\(b\) y\(c\) por mínimos cuadrados, y los probables errores de\(V\),\(t_0\) y\(r_0\).

La distancia entre los dos vértices de la hipérbola es su eje transversal, y la longitud del eje semitransversal es\(a\) − pero ¿cuál es el significado geométrico de la longitud\(b\)? Esto se discute a continuación en la siguiente subsección (sobre la hipérbola conjugada) y nuevamente en una sección posterior sobre el parámetro de impacto.

Las líneas perpendiculares al\(x\) eje y que pasan por los focos son las dos latera recta. Dado que los focos están en\((\pm ae , \ 0)\), los puntos donde la latera recta se cruzan con la hipérbola se pueden encontrar poniendo\(x = ae\) en la Ecuación a la hipérbola, y luego se encuentra que la longitud\(l\) de un recto semi latus es

\[l = a(e^2 -1 ) . \label{2.5.5} \tag{2.5.5}\]

Definición: La hipérbola conjugada

La Ecuación

\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = -1 \label{2.5.6} \tag{2.5.6}\]

es la Ecuación a la hipérbola conjugada.

La hipérbola conjugada se dibuja discontinua en la figura\(\text{II.28}\), y se ve que el significado geométrico de\(b\) es que es la longitud del eje semitransversal de la hipérbola conjugada. Es un asunto sencillo demostrar que la excentricidad de la hipérbola conjugada es\(e/\sqrt{e^2-1}\).

Definición: Las asíntotas

Las líneas\[y = \pm \dfrac{bx}{a} \label{2.5.7} \tag{2.5.7}\]

son las asíntotas de la hipérbola.

La ecuación\ ref {2.5.7} también se puede escribir

\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 0. \label{2.5.8} \tag{2.5.8}\]

Así

\[ \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = c \label{2.5.9} \tag{2.5.9}\]

es la hipérbola, las asíntotas o la hipérbola conjugada, si\(c = +1\),\(0\) o\(−1\) respectivamente. Las asíntotas se dibujan como líneas punteadas en la figura\(\text{II.28}\).

El semi ángulo ψ entre las asíntotas viene dado por

\[\tan ψ = b/a. \label{2.5.10} \tag{2.5.10}\]

Ejercicio 1

Si la excentricidad de una hipérbola es\(e\), mostrar que la excentricidad de su conjugado es\(\dfrac{e}{\sqrt{e^2 - 1}}\).

Ejercicio 1: Corolario

Nadie se sorprenderá al señalar que esto implica que, si las excentricidades de una hipérbola y su conjugado son iguales, entonces cada una es igual a\(\sqrt{2}\).

Las Directivas

Las líneas\(y = \pm a / e\) son las guías, y, al igual que con la elipse (y con una prueba similar), la hipérbola tiene la propiedad de que la relación de la distancia\(\text{PF}_2\) a un foco a la distancia\(\text{PN}\) a la directriz es constante y es igual a la excentricidad de la hipérbola. Esta relación (es decir, la excentricidad) es menor que uno para la elipse, igual a uno para la parábola, y mayor que uno para la hipérbola. No es una propiedad que va a ser de gran importancia para nuestros fines, pero vale la pena mencionar porque es una propiedad que a veces se utiliza para definir una hipérbola. Dejo al lector dibujar las orientaciones en sus posiciones correctas en figura\(\text{II.28}\).

Ecuaciones paramétricas a la hipérbola.

El lector recordará que el punto\((a \cos E, b \sin E)\) está en la elipse\((x^2/a^2) + \left( y^2/b^2 \right) = 1\) y que esto es evidente porque esta Ecuación es la\(E\) -eliminante de\(x = a \cos E\) y\(y = b \sin E\). El ángulo\(E\) tiene una interpretación geométrica como la anomalía excéntrica. Así mismo, recordando la relación\(\cosh^2 \phi − \sinh^2 \phi = 1\), será evidente que también se\((x^2 / a^2) - \left(y^2/b^2 \right) = 1\) puede obtener como el\(\phi\) −eliminante de las Ecuaciones

\[x = a \cosh \phi, \quad y = b \sinh \phi \label{2.5.11} \tag{2.5.11}\]

Estas dos Ecuaciones son, por lo tanto, las Ecuaciones paramétricas a la hipérbola, y cualquier punto que satisfagando estas dos Ecuaciones se encuentra en la La variable no\(\phi\) es un ángulo, y no tiene una interpretación geométrica análoga a la anomalía excéntrica de una elipse. Las Ecuaciones

\[x = a \sec E, \quad y = b \tan E \label{2.5.12} \tag{2.5.12}\]

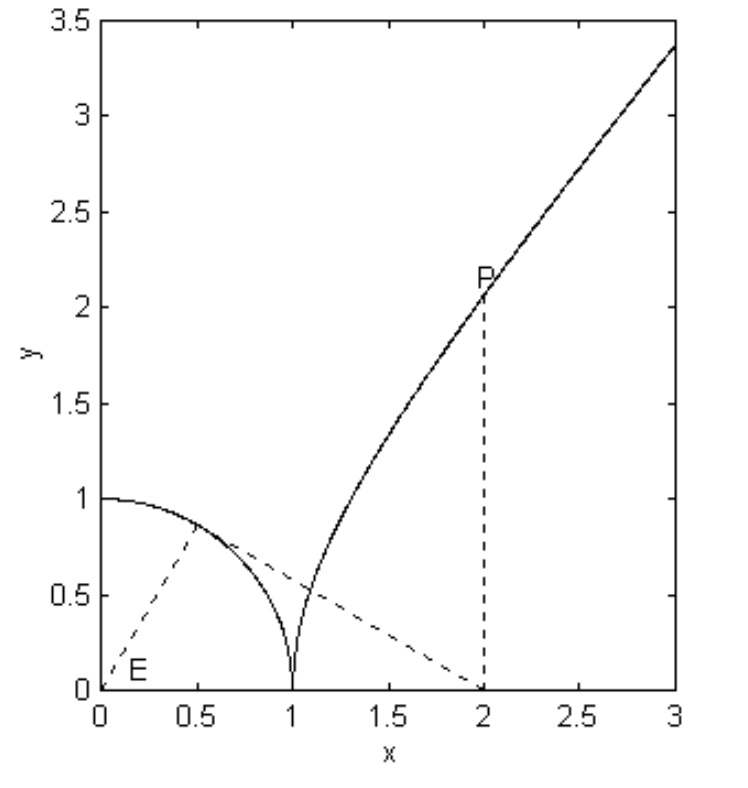
también se pueden utilizar como ecuaciones paramétricas a la hipérbola, a causa de la identidad trigonométrica\(1 + \tan^2 E = \sec^2 E\). En ese caso, el ángulo\(E\) sí tiene una interpretación geométrica (aunque no particularmente interesante) en relación con el círculo auxiliar, que es el círculo de radio a centrado en el origen. El significado del ángulo debe ser evidente a partir de la figura\(\text{II.29}\), en la que\(E\) se encuentra el ángulo excéntrico correspondiente al punto\(\text{P}\).

\(\text{FIGURE II.29}\)

Parámetro de impacto

Una partícula que viaja muy rápido bajo la acción de una fuerza de atracción cuadrada inversa (como un meteorito interestelar o cometa -si hay tales cosas- que pasa por el Sol, o un electrón en las proximidades de un núcleo atómico cargado positivamente) se moverá en un camino hiperbólico. Esto lo demostramos en un capítulo posterior, además de discutir la velocidad necesaria. Podemos imaginar la partícula inicialmente acercándose desde una gran distancia a lo largo de la asíntota en la esquina inferior derecha de la figura\(\text{II.30}\). A medida que se acerca al foco, ya no se mueve a lo largo de la asíntota sino a lo largo de un brazo de la hipérbola.

\(\text{FIGURE II.30}\)

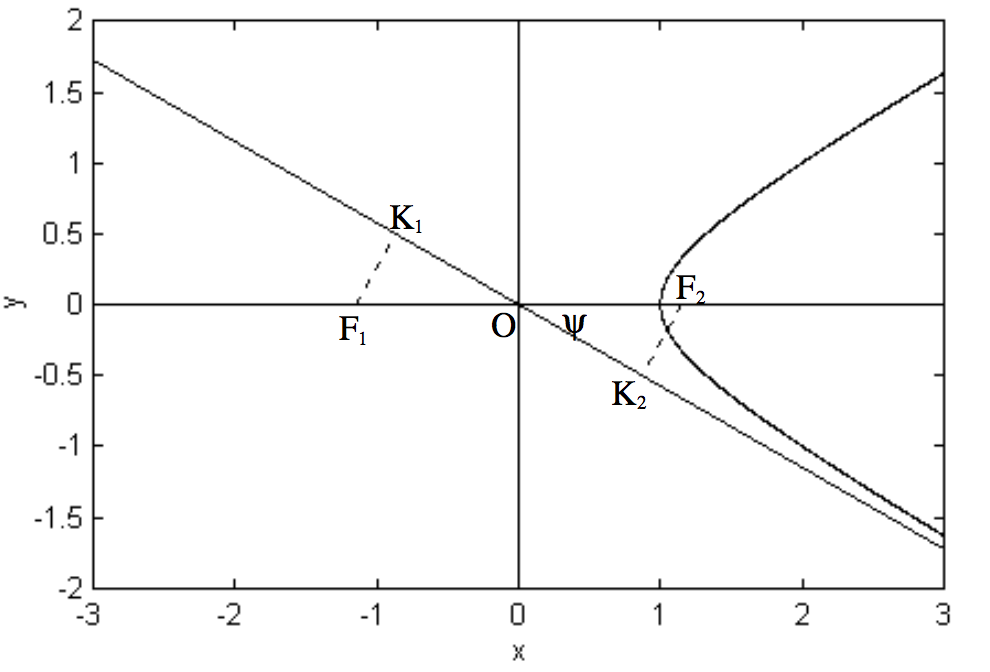
La distancia\(\text{K}_2 \ \text{F}_2\), que es la distancia por la que la partícula habría perdido\(\text{F}_2\) en ausencia de una fuerza de atracción, se denomina comúnmente el parámetro de impacto. De igual manera, si la fuerza hubiera sido una fuerza repulsiva (por ejemplo, supongamos que la partícula móvil fuera una partícula cargada positivamente y hubiera un centro de repulsión en\(\text{F}_1\),\(\text{F}_1\text{K}_1\) sería el parámetro de impacto. Claramente,\(\text{F}_1\text{K}_1\) y\(\text{F}_2\text{K}_2\) son iguales en longitud. El símbolo que a menudo se usa en la teoría de la dispersión, ya sea en la mecánica celeste o en la física de partículas, es\(b\) -pero ¿es esto\(b\) lo mismo\(b\) que entra en la Ecuación a la hipérbola y que es igual al eje semi mayor de la hipérbola conjugada?

\(\text{OF}_2 = ae\), y por lo tanto\(\text{K}_2\text{F}_2 = ae \sin ψ\). Esto, en conjunto con\(\tan ψ = b/a\) y\(b^2 = a^2 (e^2 − 1)\), pronto demostrará que el parámetro de impacto es efectivamente el mismo con el\(b\) que estamos familiarizados, y que por lo tanto\(b\) es un símbolo muy adecuado para usar como parámetro de impacto.

Tangentes a la hipérbola

Usando los mismos argumentos que para la elipse, el lector debería encontrar fácilmente esas líneas de la forma

\[y = mx \pm \sqrt{a^2 m^2 - b^2} \tag{2.5.13} \label{2.5.13}\]

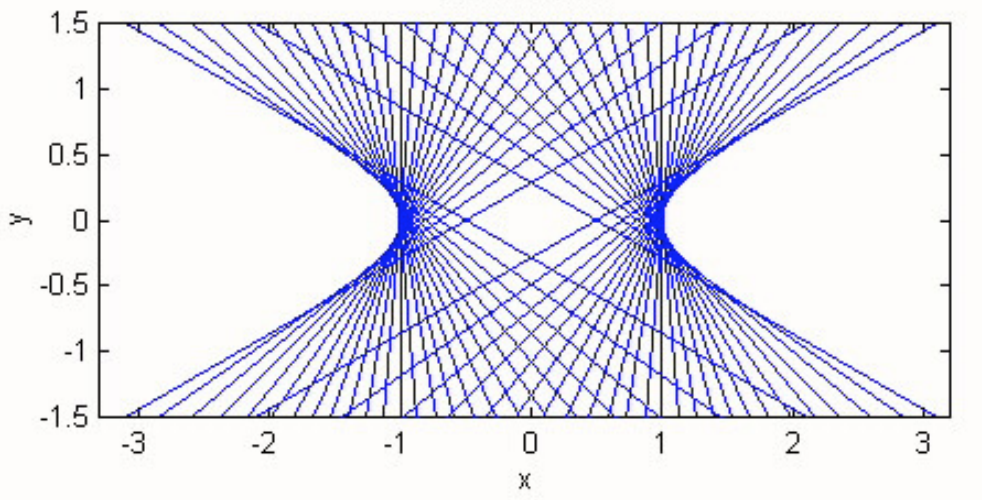
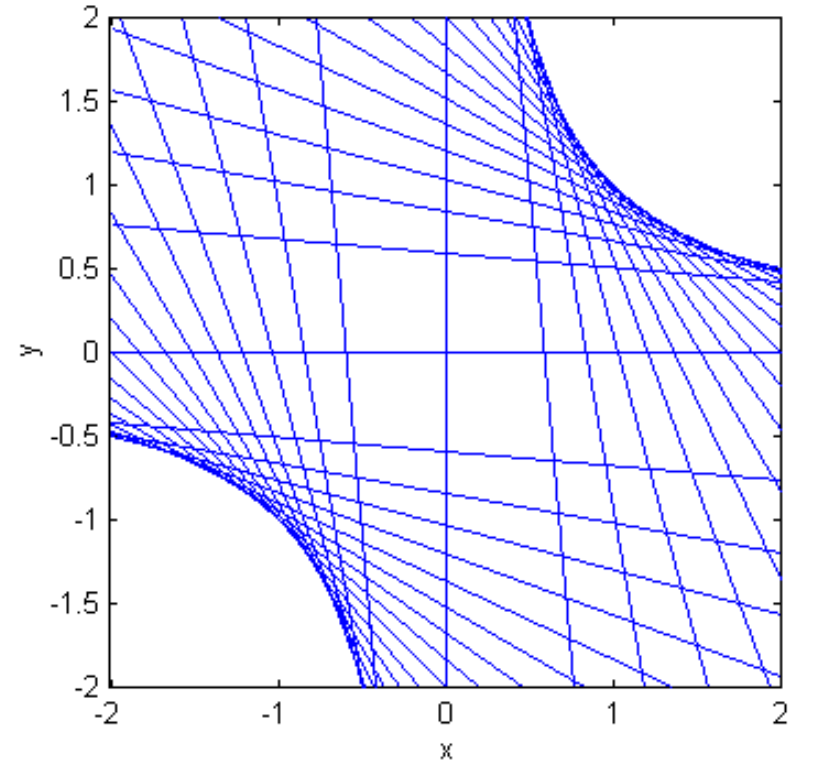
son tangentes a la hipérbola. Esto se ilustra en figura\(\text{II.33}\) para una hipérbola con\(b = a /2\), con tangentes dibujadas con pendientes\(30^\circ\) a\(150^\circ\) en pasos de\(5^\circ\). (Las asíntotas tienen\(ψ = 26^\circ 34^\prime\).) (Lo siento, pero no hay cifras\(\text{II.31}\) ni\(\text{II.32}\) - ¡problemas informáticos!)

\(\text{FIGURE II.31}\)

Asimismo, a partir de argumentos similares utilizados para la elipse, se encuentra que la tangente a la hipérbola en el punto\((x ,y)\) es

\[\frac{x_1x}{a^2} - \dfrac{y_1y}{b^2} = 1. \label{2.5.14} \tag{2.5.14}\]

Círculo Director

En cuanto a la elipse, y con una derivación similar, el locus de los puntos de intersección de tangentes perpendiculares es un círculo, llamado círculo director, que es de radio\(√(a^2 − b^2 )\). Esto no es de particular importancia para nuestros propósitos, pero el lector que esté interesado tal vez quiera probarlo por el mismo método que se hizo para el círculo director de la elipse, y tal vez quiera intentar dibujar el círculo y algunas tangentes. Si\(b > a\), es decir si\(ψ > 45^\circ\) y el ángulo entre las asíntotas es mayor que\(90^\circ\), el círculo director no es real y por supuesto no es posible dibujar tangentes perpendiculares.

Hipérbola Rectangular

Si el ángulo entre las asíntotas es\(90^\circ\), la hipérbola se llama hipérbola rectangular. Para tal hipérbola,\(b = a\), la excentricidad es\(√2\), el círculo director es un punto, es decir, el origen, y las tangentes perpendiculares sólo se pueden dibujar a partir de las asíntotas.

La Ecuación a una hipérbola rectangular es

\[x^2 - y^2 = a^2 \label{2.5.15} \tag{2.5.15}\]

y las asíntotas están en\(45^\circ\) el\(x\) eje.

Dejar\(\text{O}x^\prime, \ \text{O}y^\prime\) ser un conjunto de ejes en\(45^\circ\) el\(x\) eje. (Es decir, son las asíntotas de la hipérbola rectangular.) Luego se encuentra la Ecuación a la hipérbola rectangular referida a sus asíntotas como ejes de coordenadas por las sustituciones

\[\pmatrix{x \\ y} = \pmatrix{\cos 45^\circ & \sin 45^\circ \\ - \sin 45^\circ & \cos 45^\circ} \pmatrix{x^\prime \\ y^\prime} \tag{2.5.16} \label{2.5.16}\]

en\(x^2 − y^2 = a^2\). Esto da como resultado la Ecuación

\[x^\prime y^\prime = \frac{1}{2} a^2 = c^2 , \quad \text{where} \quad c= a/\sqrt{2}, \label{2.5.17} \tag{2.5.17}\]

para la Ecuación a la hipérbola rectangular referida a sus asíntotas como ejes de coordenadas. La interpretación geométrica de\(c\) se muestra en la figura\(\text{II.32}\), que se dibuja para\(c = 1\), y hemos llamado los ejes de coordenadas\(x\) y\(y\). La longitud del eje semitransversal es\(c \sqrt{2}\).

\(\text{FIGURE II.32}\)

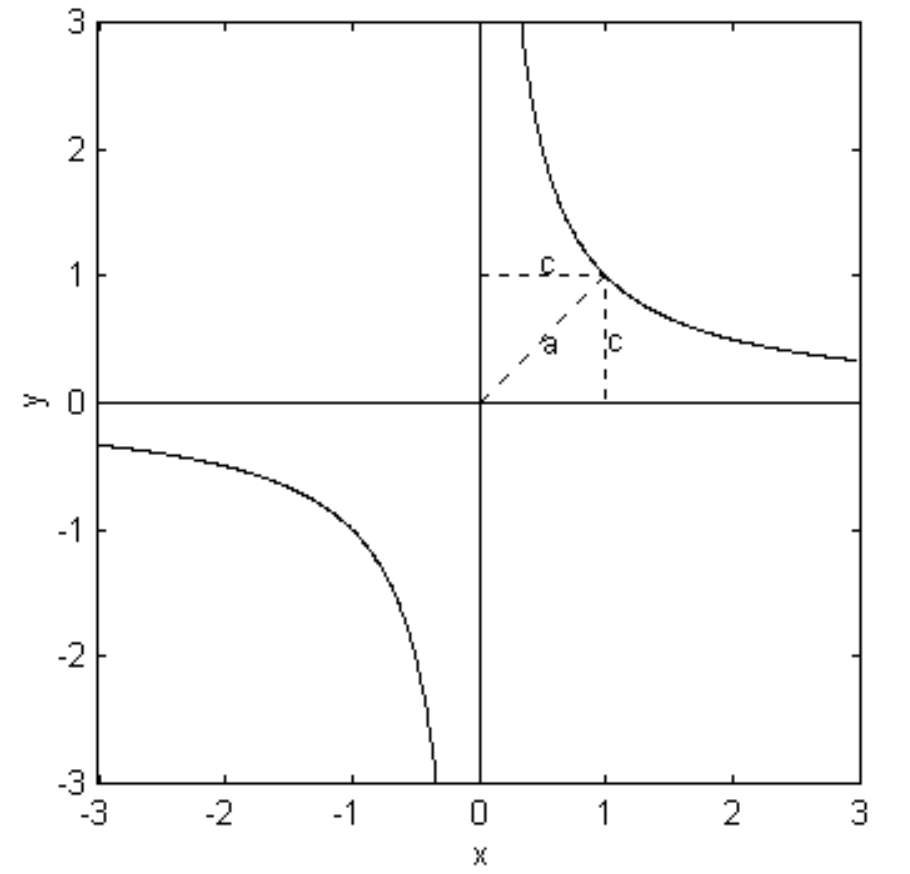
La ecuación simple\(y = 1/x\) es una hipérbola rectangular y de hecho es esta Ecuación la que se muestra en la figura\(\text{II.32}\).

Se deja al lector demostrar que las Ecuaciones paramétricas a la hipérbola rectangular\(xy = c^2\) (hemos caído los primos) son\(x = ct, \ y = c/t\), que las líneas de la forma\(y=mx \pm 2c \sqrt{-m}\) son tangentes a\(xy = c^2\) (figura II.35, dibujado con pendientes de\(90^\circ\) a\(180^\circ\) en pasos de\(5^\circ\)), y que la tangente en\((x_1 , y_1 )\) es\(x_1y + y_1x = 2c\).

\(\text{FIGURE II.33}\)

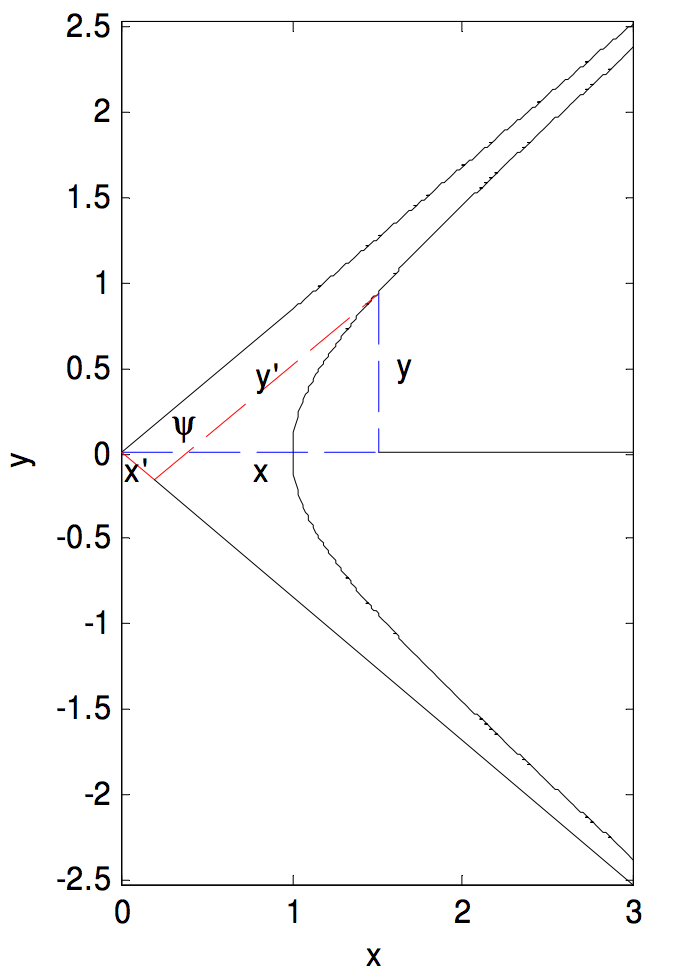
Ecuación de una hipérbola referida a sus asíntotas como ejes de coordenadas

Hemos demostrado que la Ecuación a una hipérbola rectangular referida a sus asíntotas como ejes de coordenadas es\(x^\prime y^\prime = \frac{1}{2} a^2 = c^2\). De hecho la Ecuación\(x^\prime y^\prime = c^2\) es la Ecuación a cualquier hipérbola (centrada en\((0 ,\ 0)\)), no necesariamente rectangular, cuando se refiere a sus asíntotas como ejes de coordenadas, donde\(c^2 = \frac{1}{4} (a^2 + b^2)\) En la siguiente figura he dibujado una hipérbola y un punto sobre la hipérbola cuyas coordenadas con respecto a la los ejes horizontal y vertical son\((x , \ y)\), y cuyas coordenadas con respecto a las asíntotas son\((x^\prime , y^\prime)\). He mostrado las distancias\(x\) y\(y\) con líneas discontinuas azules, y las distancias\(x^\prime\) y\(y^\prime\) con líneas discontinuas rojas. El semiángulo entre las asíntotas es\(ψ\).

La Ecuación a la hipérbola referida a los ejes horizontal y vertical es

\[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1. \label{2.5.18} \tag{2.5.18}\]

Del dibujo, vemos que

\[x = (x^\prime + y^\prime) \cos ψ, \quad y = (y^\prime - x^\prime) \sin ψ. \label{2.5.19a,b} \tag{2.5.19a,b}\]

Si los sustituimos en Ecuación\(\ref{2.5.18}\), y también hacemos uso de la relación\(\tan ψ = b/a\) (Ecuación\(\ref{2.5.10}\)), llegamos a la Ecuación a la hipérbola referida a las asíntotas como ejes de coordenadas:

\[x^\prime y^\prime = \frac{1}{4}(a^2 + b^2) = c^2 . \label{2.5.20} \tag{2.5.20}\]

Ecuación polar a la hipérbola

Encontramos las ecuaciones polares a la elipse y a la parábola de diferentes maneras. Ahora regresa y mira ambos métodos y usa cualquiera (o ambos) para mostrar que la Ecuación polar a la hipérbola (enfoque como polo) es

\[r = \frac{l}{1+ e \cos \theta}. \tag{2.5.21} \label{2.5.21}\]

Esta es la Ecuación polar a cualquier sección cónica - la cual está determinada únicamente por el valor de\(e\). También deberías preguntarte qué es lo que representa la Ecuación

\[r = \frac{l}{1-e \cos \theta}. \label{2.5.22} \tag{2.5.22}\]

Intente bosquejarlo para diferentes valores de\(e\).