5.7: Potencial

Si se requiere trabajo para mover una masa de punto\(\text{A}\) a punto\(\text{B}\), se dice que hay una diferencia de potencial gravitacional entre\(\text{A}\) y\(\text{B}\), con\(\text{B}\) estar en el potencial más alto. El trabajo requerido para mover la masa unitaria de\(\text{A}\) a\(\text{B}\) se llama la diferencia de potencial entre\(\text{A}\) y\(\text{B}\). En unidades SI se expresa en\(\text{J kg}^{−1}\).

Solo hemos definido la diferencia de potencial entre dos puntos. Si queremos definir el potencial en un punto, es necesario definir arbitrariamente el potencial en un punto determinado para que sea cero. Podríamos, por ejemplo, definir el potencial a nivel del piso para que sea cero, en cuyo caso el potencial a una altura\(h\) por encima del piso es\(gh\); igualmente podemos optar por definir el potencial a nivel de la mesa de laboratorio para que sea cero, en cuyo caso el potencial a una altura\(z\) por encima del la parte superior del banco es\(gz\). Debido a que el valor del potencial en un punto depende de donde definamos el cero de potencial, a menudo se ve que el potencial en algún momento es igual a alguna expresión matemática más una constante arbitraria. El valor de la constante se determinará una vez que hayamos decidido dónde queremos definir el potencial cero.

En la mecánica celeste es habitual asignar potencial cero a todos los puntos a una distancia infinita de cualquier cuerpo de interés.

Supongamos que decidimos definir el potencial en el punto\(\text{A}\) para ser cero, y que el potencial en\(\text{B}\) es entonces\(ψ\)\(\text{J kg}^{−1}\). Si movemos una masa puntual\(m\) de\(\text{A}\) a\(\text{B}\), tendremos que hacer una cantidad de trabajo igual a\(mψ \ \text{J}\). La energía potencial de la masa\(m\) cuando está en\(\text{B}\) es entonces\(mψ\). En estas notas, usualmente utilizaré el símbolo\(ψ\) para el potencial en un punto, y el símbolo\(V\) para la energía potencial de una masa en un punto.

Al mover una masa puntual de\(\text{A}\) a\(\text{B}\), no importa qué ruta se tome. Todo lo que importa es la diferencia de potencial entre\(\text{A}\) y\(\text{B}\). Las fuerzas que tienen la propiedad de que el trabajo requerido para moverse de un punto a otro es independiente de la ruta se denominan fuerzas conservadoras; las fuerzas gravitacionales son conservadoras. El potencial en un punto es una cantidad escalar; no tiene una dirección particular asociada a ella.

Si requiere trabajo para mover un cuerpo de punto\(\text{A}\) a punto\(\text{B}\) (es decir, si hay una diferencia de potencial entre\(\text{A}\) y\(\text{B}\), y\(\text{B}\) está a un potencial mayor que\(\text{A}\)), esto implica que debe haber un campo gravitacional dirigido de\(\text{B}\) a\(\text{A}\).

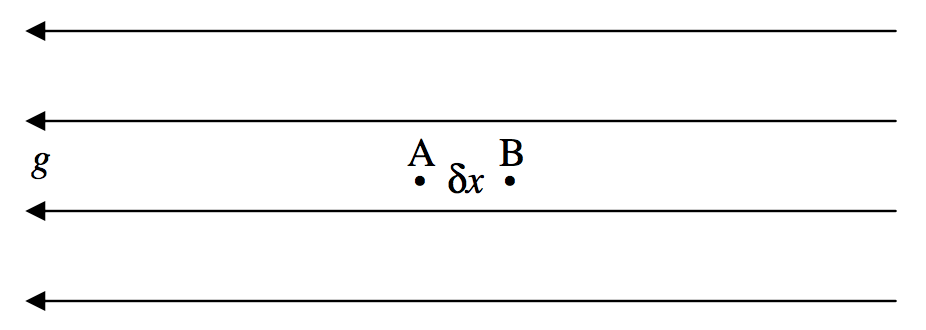
\(\text{FIGURE V.22}\)

La figura\(\text{V.22}\) muestra dos puntos,\(\text{A}\) y\(\text{B}\), una\(δx\) distancia entre sí, en una región del espacio donde el campo gravitacional se\(g\) dirige en\(x\) dirección negativa. Supondremos que la diferencia de potencial entre\(\text{A}\) y\(\text{B}\) es\(δψ\). Por definición, el trabajo requerido para mover la masa unitaria de\(\text{A}\) a\(\text{B}\) es\(δψ\). También por definición, la fuerza sobre la masa unitaria es\(g\), de manera que el trabajo realizado sobre la masa unitaria es\(gδx\). Así tenemos

\[g = - \frac{dψ}{dx}. \label{5.7.1} \tag{5.7.1}\]

El signo menos indica que, mientras el potencial aumenta de izquierda a derecha, el campo gravitacional se dirige hacia la izquierda. En palabras, el campo gravitacional es menos el gradiente potencial.

Este fue un ejemplo unidimensional. En una sección posterior, cuando discutamos el operador vectorial\(\nabla\), escribiremos Ecuación\(\ref{5.7.1}\) en su forma tridimensional

\[\textbf{g} = - \textbf{grad}ψ = - \nabla ψ. \label{5.7.2} \tag{5.7.2}\]

Si bien\(ψ\) en sí misma es una cantidad escalar, no teniendo propiedades direccionales, su gradiente es, por supuesto, un vector.