6.7: Precesión
- Page ID
- 131179
El Primer Punto de Aries es el punto donde la eclíptica cruza el ecuador en el punto ocupado por el Sol en el equinoccio de marzo. Es el punto a partir del cual se miden las ascensiones derechas. Hasta ahora lo hemos tratado como si estuviera fijo relativo a las estrellas, aunque de vez en cuando hemos insinuado que esto no es exactamente así. En efecto hemos dicho que es esencial, al afirmar la correcta ascensión y declinación de una estrella, declarar la fecha del equinoccio al que se refiere.
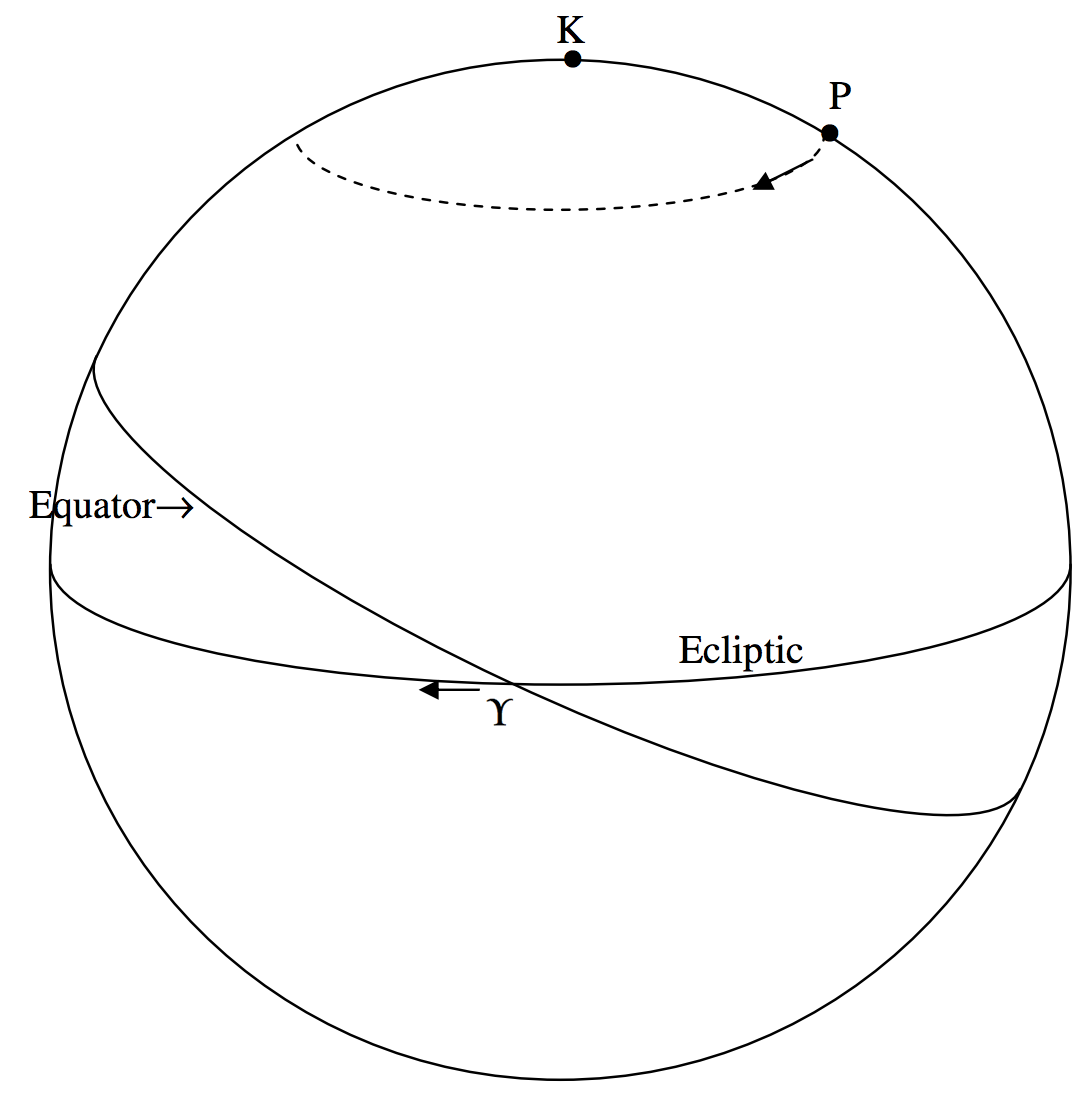
En figura\(\text{VI.6}\), he dibujado la eclíptica horizontalmente, y el ecuador celeste inclinado en un ángulo de\(23^\circ .4\). Se puede ver el polo norte de la eclíptica,\(\text{K}\), y el polo celeste norte\(\text{P}\). El gran círculo\(\text{P} \Upsilon\) (no dibujado) es el colure equinoccial, y la ascensión correcta de\(\Upsilon\) es\(0^h\). La recta ascensión y declinación de\(\text{K}\) son\(18^h\)\(+66^\circ .6\), que es un punto entre las estrellas\(δ\) y\(ζ\) Draconis.
Ni el polo celeste norte\(\text{P}\) ni el “Primer Punto de Aries”\(\Upsilon\) son fijos, sin embargo. El polo celeste norte\(\text{P}\) describe un pequeño círculo de radio\(23^\circ .4\) alrededor\(\text{K}\), y el equinoccio retrocede hacia el oeste a lo largo de la eclíptica en un período de 25.800 años. Esta moción, llamada la precesión de los equinoccios (o simplemente “precesión” para abreviar) no es del todo uniforme, pero es casi así y será tratada como tal en esta sección. El ciclo completo de 25.800 años corresponde a una regresión hacia el oeste de a\(\Upsilon\) lo largo de la eclíptica de\(50^{\prime \prime}.2\) por año o\(0^{\prime \prime}.137\) por día. El componente de ese movimiento a lo largo del ecuador celeste es\(0^{\prime \prime}.137\)\(\cos 23^\circ .4 = 0^{\prime \prime} .126 = 0^{\text{s}} .008\) por día. Es por ello que la duración del día sideral medio (que se define como el intervalo entre dos tránsitos meridianos superiores consecutivos del primer punto de Aries) es\(0^{\text{s}} .008\) más corta que el período de rotación sideral de la Tierra.
La precesión de\(\text{P}\) alrededor\(\text{K}\) significa que todo el sistema de coordenadas ecuatoriales (ascensión derecha y declinación) se mueve continuamente, y las ascensiones y declinaciones correctas de todas las estrellas están cambiando continuamente. No importa dónde\(\text{P}\) esté en su recorrido\(\text{K}\), sin embargo, las coordenadas ecuatoriales de\(\Upsilon\) y de\(\text{K}\) son siempre\(0^{\text{h}}\),\(0^{\text{o}}\) y\(18^\text{h}\),\(+66^\text{o} .5\). No obstante, las coordenadas ecuatoriales de las estrellas deben referirse siempre al equinoccio y al ecuador de una época declarada.
\(\text{FIGURE VI.6}\)
Durante gran parte del siglo XX, fue la época a la que se refieren muchos catálogos y atlas\(\text{B}1950.0\). Ese es el comienzo del Año Besseliano de 1950, en el instante (poco antes de la medianoche de la noche de 1949 Dic 31/1950 Ene 1) cuando fue la ascensión correcta del Sol Medio\(18^\text{h} 40^\text{m}\). La mayoría de los catálogos desde 1984 han referido ascensiones y declinaciones correctas al equinoccio medio y ecuador de\(\text{J}2000.0\). Ese es el inicio del Año Juliano 2000, en el instante en que la Hora Media de Greenwich (UT) indicó la medianoche. Por ejemplo, en los catálogos más antiguos, la recta ascensión y declinación de Arcturus se daría como
\[α_{1950.0} = 14^\text{h} \quad 13^\text{m}.4 \quad δ_{1950.0} = +19^\circ 26^\prime,\]
mientras que en los catálogos más recientes se dan como
\[α_{2000.0} = 14^\text{h} \quad 15^\text{m}.8 \quad δ_{2000.0} = +19^\circ 11^\prime . \]
De esta manera se puede observar que para un trabajo preciso la diferencia no es en absoluto despreciable, y en general no es útil declarar las coordenadas ecuatoriales de un objeto sin precisar también la época del equinoccio y ecuador a los que se refieren las coordenadas. Por supuesto, al fijar los círculos de un telescopio para las observaciones nocturnas, lo que se necesita es la ascensión y declinación correctas referidas al equinoccio y al ecuador de la fecha —es decir, para la fecha en cuestión—. Por lo tanto, es fundamental que un observador práctico sepa corregir la precesión.
\(\text{FIGURE VI.7}\)
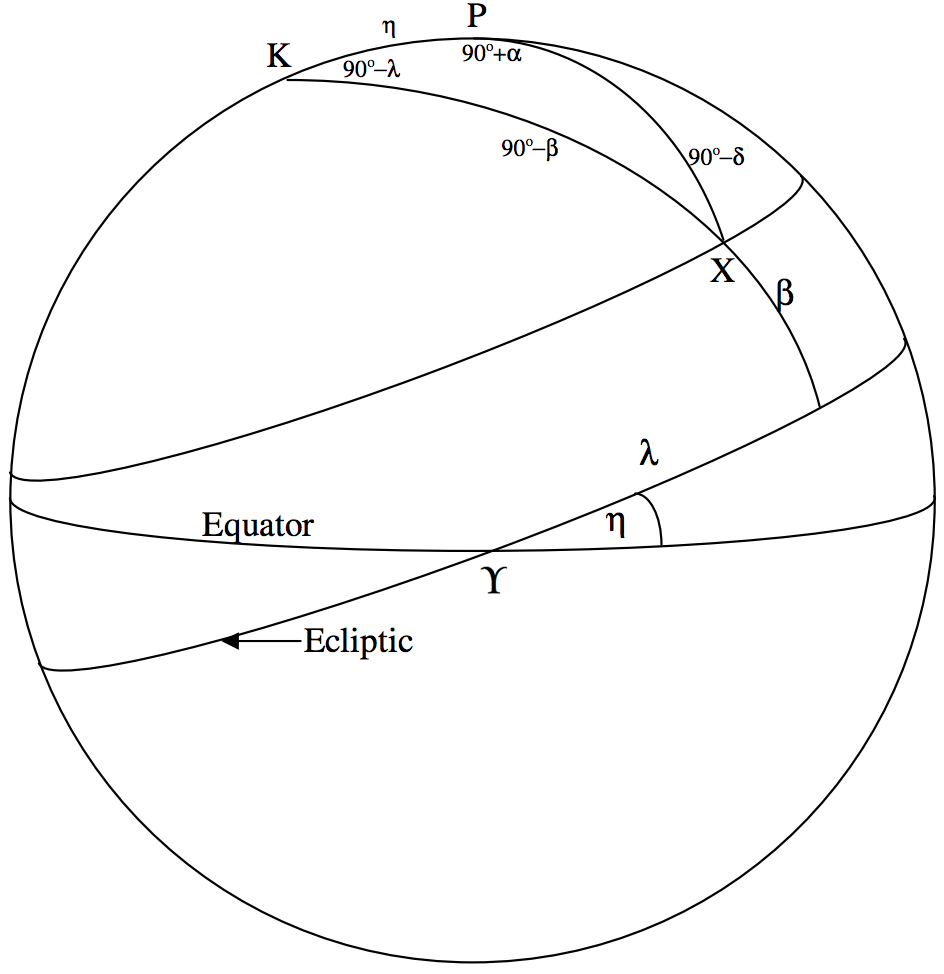
Aplicar la fórmula coseno (Ecuación 3.5.2) al triángulo\(\text{PKX}\) para obtener
\[\sin δ = \cos η \sin β + \sin η \cos β \sin λ. \label{6.7.1} \tag{6.7.1}\]
Dado que\(\Upsilon\) está retrocediendo por la eclíptica, la longitud eclíptica\(λ\) de la estrella\(\text{X}\) va en aumento. Si está aumentando a una tasa\(\dot{λ}\)\((= 50^{\prime \prime}.2\) por año), la tasa de cambio de su declinación se puede obtener por diferenciación de la Ecuación\(\ref{6.7.1}\) respecto al tiempo, teniendo en cuenta que\(β\) y\(η\) son constantes:
\[\cos δ \dot{δ} = \sin η \cos β \cos λ \dot{λ} . \label{6.7.2} \tag{6.7.2}\]
Pero\((\cos β \cos λ)/\cosδ\) se obtiene de la fórmula sinusoidal (Ecuación 3.5.1):
\[\frac{\cos β}{\cos α} = \frac{\cos δ}{\cos λ} . \label{6.7.3} \tag{6.7.3}\]
De ahí que obtengamos para la tasa de cambio de declinación de una estrella por precesión:
\[\dot{δ} = \dot{λ} \sin η \cos α . \label{6.7.4} \tag{6.7.4}\]
Para obtener la tasa de cambio de ascensión derecha, podemos escribir la Ecuación\(\ref{6.7.3}\) como
\[\cos α = \cos β \sec δ \cos λ \label{6.7.5} \tag{6.7.5}\]
y luego diferenciar con respecto al tiempo:
\[-\sin α \dot{α} = \cos β \sec δ (\tan δ \dot{δ} \cos λ - \sin λ \dot{λ}), \label{6.7.6} \tag{6.7.6}\]
que voy a escribir como
\[-\sin α \dot{α} = \cos β \sec δ \cos λ ( \tan δ \dot{δ} - \tan λ \dot{λ}). \label{6.7.7} \tag{6.7.7}\]
Podemos obtener\(\cos β \sec δ \cos λ\) de Ecuación\(\ref{6.7.5}\), y por supuesto que tenemos\(δ\) de Ecuación\(\ref{6.7.4}\), pero aún necesitamos encontrar una expresión para\(\tan λ\) en términos de coordenadas ecuatoriales. Podemos hacer esto desde la fórmula cotangente (Ecuación 3.5.4), en la que el ángulo interior es\(90^\circ + α\) y el lado interno es\(η\):
\[-\cos η \sin α = \sin η \tan δ - \cos α \tan λ . \label{6.7.8} \tag{6.7.8}\]
Al sustituir las Ecuaciones\ ref {6.7.4},\ ref {6.7.5} y\ ref {6.7.8} en Ecuación\ ref {6.7.7} obtenemos, después de una cantidad muy pequeña de álgebra, para la tasa de cambio de ascensión derecha de una estrella por precesión:
\[\dot{α} = \dot{λ} ( \cos η + \sin α \tan δ \sin η). \label{6.7.9} \tag{6.7.9}\]
Con\(\dot{λ} = 50^{\prime \prime}.2\) por año y\(η = 23^\circ .4\), Ecuaciones\ ref {6.7.4} y\ ref {6.7.9} se convierten
\[\dot{δ} = 19^{\prime \prime} .9 \cos α \quad \text{per year} \label{6.7.10} \tag{6.7.10}\]
y\[\dot{α} = 46^{\prime \prime} .1 + 19^{\prime \prime} .9 \sin α \tan δ \quad \text{per year} \label{6.7.11} \tag{6.7.11}\]
o\[\dot{α} = 3^{s} .07 + 1^{\text{s}} .33 \sin α \tan δ \quad \text{per year}. \label{6.7.12} \tag{6.7.12}\]
Estas fórmulas deben ser adecuadas para todos menos cálculos muy precisos.
Problema: Usa Ecuaciones\ ref {6.7.10} y\ ref {6.7.12} para verificar los datos sobre Arcturus — ¡y por favor avíseme si no está bien!
En la época de Hipparcos (quien descubrió el fenómeno de la precesión desde hace mucho tiempo como el siglo II a.C.), el equinoccio de primavera estaba en la constelación Aries —de hecho en su límite oriental. De ahí que se le denominara el Primer Punto de Aries. A lo largo de los siglos, la precesión ha llevado al equinoccio hacia el oeste a través de la constelación Aries, y debido a esto, junto a la forma en que se fijaron formalmente los límites de las constelaciones en 1928, el equinoccio se encuentra ahora cerca del límite occidental de Piscis y está a solo unos pocos grados de Acuario. Todavía se le llama, sin embargo, por su nombre tradicional del Primer Punto de Aries. Por cierto, la eclíptica en realidad pasa por la constelación de Ofiuco, que no es uno de los doce tradicionales “Signos del Zodiaco”, y a veces se dice que esto es resultado de la precesión a lo largo de los siglos. Este no es el caso. La precesión no altera el plano de la eclíptica, y la eclíptica continúa pasando por las mismas constelaciones independientemente de dónde se encuentre el equinoccio a lo largo de ella. La inclusión de Ofiuco es simplemente el resultado de la forma en que se fijaron formalmente los límites de las constelaciones en 1928.
La causa física de la precesión
El movimiento diario de las estrellas alrededor del polo celeste norte es, por supuesto, un reflejo de la rotación de la Tierra sobre su eje; y el movimiento anual del Sol a lo largo de la eclíptica, que se inclina\(23^\circ .4\) hacia el ecuador celeste, es un reflejo del movimiento orbital anual de la Tierra alrededor del Sol, el plano del ecuador rotacional de la Tierra estando inclinado\(23^\circ .4\) hacia el plano de su órbita, es decir, hacia la eclíptica. Si bien esta oblicuidad de\(23^\circ .4\) es aproximadamente constante, la dirección del eje de rotación de la Tierra no es fija, sino que precede alrededor de lo normal al plano eclíptico con un periodo de 25.800 años.
Desde el punto de vista de la mecánica clásica, la Tierra es una cima simétrica oblata. Es decir, tiene un eje de simetría y dos de sus principales momentos de inercia son iguales y son menores que el momento de inercia alrededor del eje de simetría. Los fenómenos de precesión de tal cuerpo son bien entendidos y se estudian en cursos de mecánica clásica. Sin embargo, es necesario tener claro en la mente la distinción entre la precesión sin par y la precesión inducida por el par.
El fenómeno de la precesión sin par es la precesión que ocurre cuando una capota simétrica gira alrededor de un eje que no coincide con su eje de simetría y gira libremente sin pares externos que actúan sobre ella. En tales circunstancias, el vector de momento angular se fija en magnitud y dirección. El eje de simetría precede alrededor del vector de momento angular fijo mientras que el eje instantáneo de rotación precede alrededor del eje de simetría. La rotación de la Tierra efectivamente exhibe este tipo de comportamiento, pero esta no es la precesión de la que estamos hablando en relación con la precesión de los equinoccios. El eje instantáneo de rotación de la Tierra está a solo unos pocos metros de su eje de simetría y el período de la precesión sin par es de aproximadamente 432 días. Esto da lugar a un fenómeno conocido como variación de latitud, y da como resultado que las latitudes de ubicaciones de la superficie de la Tierra varíen cuasi-periódicamente con una amplitud de menos de una quinta parte de un segundo de arco. La precesión de los equinoccios que hemos estado discutiendo en esta sección es algo completamente diferente.
La figura de la Tierra es aproximadamente un esferoide oblato. Si llamamos al radio ecuatorial\(a\) y al radio polar\(c\), la elipticidad geométrica\((a − c)/ a\) es aproximadamente\(1/297.0\). Si llamamos a los correspondientes momentos principales de inercia\(A\) y\(C\),\((C − A)/ A\) se trata de la elipticidad dinámica\(1/305.1\). El ecuador de la Tierra está inclinado a la eclíptica, y, debido a la protuberancia ecuatorial, la Tierra que gira está sujeta a pares tanto del Sol como de la Luna (cuya órbita está inclinada a la eclíptica en unos 5 grados). La magnitud del par es proporcional al diámetro de la Tierra por el gradiente del campo gravitacional\(2GM/r^3\), y la dirección del vector de par es perpendicular al vector de momento angular.
Ejercicio\(\PageIndex{1}\)
Busca las masas del Sol y la Luna, y sus distancias medias de la Tierra. Demuestre que\(M/r^3\) para la Luna es aproximadamente el doble que para el Sol. Así, el par sobre la Tierra ejercido por la Luna es aproximadamente el doble del par ejercido por el Sol.
Ahora bien, si una cima simétrica gira alrededor de su eje de simetría con momento angular\(\textbf{L}\) y si está sujeta a un par externo\(\boldsymbol{\tau}\), su momento angular cambiará (no en magnitud, sino en dirección), y\(\textbf{L}\) precederá con una velocidad angular\(\boldsymbol{\Omega}\) dada por
\[\boldsymbol{\tau} = \boldsymbol{\Omega} \times \textbf{L}. \label{6.7.13} \tag{6.7.13}\]
La ecuación\ ref {6.7.13} no da la dirección de\(\boldsymbol{\Omega}\) singularmente — eso depende de las condiciones iniciales. La figura\(\text{VI.8}\) ilustra la situación.
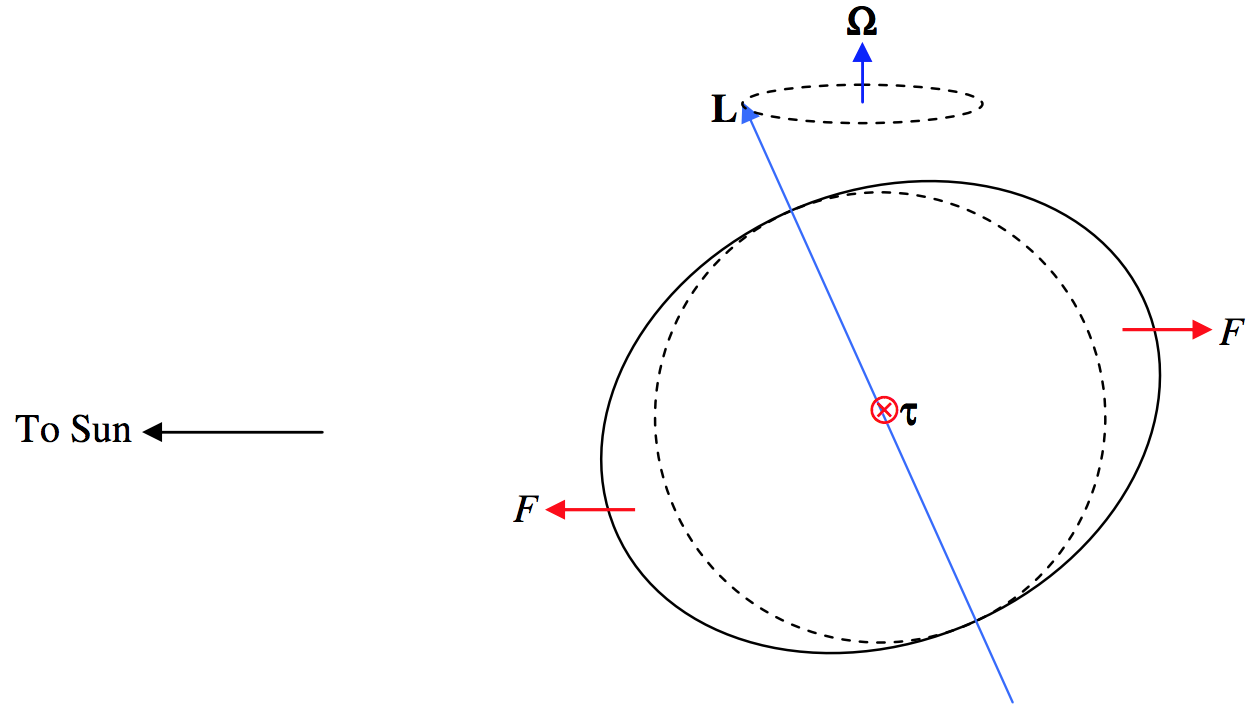
\(\text{FIGURE VI.8}\)
El bulto ecuatorial es muy exagerado. La figura se dibuja en un marco de referencia que gira alrededor del Sol con la Tierra, por lo que no hay fuerza gravitacional neta sobre la Tierra (la atracción gravitacional del Sol es contrarrestada por la fuerza centrífuga). En este marco, hay una pequeña fuerza\(F\) que actúa hacia el Sol en la protuberancia orientada al sol, y una fuerza igual que actúa alejándose del Sol en el lado opuesto. Esto equivale a un par de magnitud\(\tau = Fd \sin η\), donde\(η\) está la oblicuidad de la eclíptica y\(d\) es el diámetro de la Tierra. Así, si igualamos las magnitudes de ambos lados de la Ecuación\ ref {6.7.13}, obtenemos para la velocidad angular de la precesión
\[\Omega = Fd / L , \label{6.7.14} \tag{6.7.14}\]
que es independiente de\(η\). Esto, entonces es la causa de la precesión de los equinoccios, salvo que, a efectos de figura\(\text{VI.8}\), me referí sólo al Sol. Tú mismo has calculado que la influencia de la Luna es aproximadamente el doble que la del Sol, y el efecto combinado de la Luna y el Sol se llama la precesión luni-solar. Hay una pequeña precesión adicional resultante de la influencia de los otros planetas en el sistema solar.