6.11: Soluciones
- Page ID
- 131180
6.11.1
Creo que lo primero que haría, sería convertir las coordenadas a grados y decimales (o tal vez incluso radianes y decimales, aunque lo hago a continuación en grados y decimales):
Antares:\(α = 247.375 \quad δ = -26.433\)
Deneb\(α = 309.400 \quad δ = +45.283\)
Ya hicimos un problema similar en el Capítulo 3, Sección 3.5, Ejemplo 2, así que no lo volveré a hacer. Yo hago la respuesta:
Un polo:\(α = 11^\text{h} 47^\text{m} .3 \quad δ = + 56^\circ 11^\prime\)
el otro polo:\(α = 23^\text{h} 47^\text{m} .3 \quad δ = + 123^\circ 49^\prime\)
6.11.2
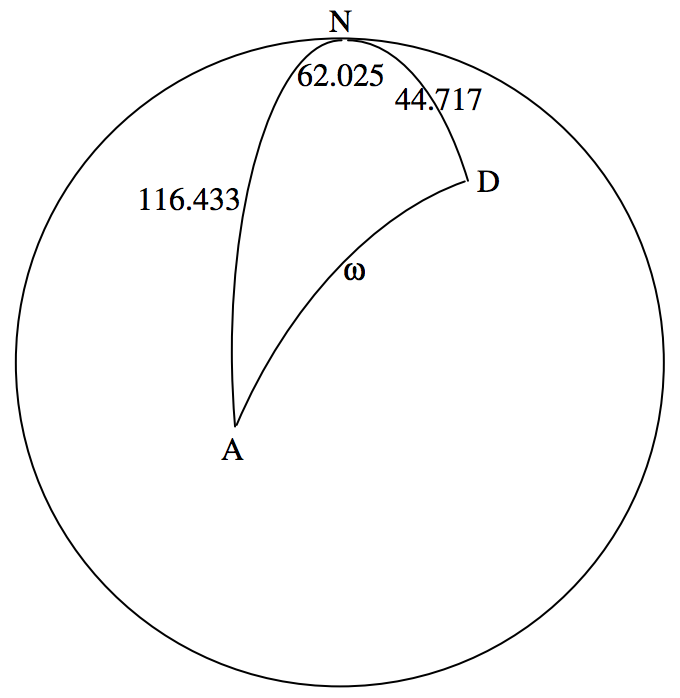
He dibujado el Polo Celestial Norte\(\text{N}\), y los colures de\(\text{N}\) a Antares (\(\text{A}\)) y a Deneb (\(\text{D}\)), junto con sus distancias polares norte en grados. También he marcado la diferencia entre sus ascensiones derechas, en grados. Podemos calcular inmediatamente, a partir de la regla coseno para triángulos esféricos, Ecuación 3.5.2, la distancia angular\(ω\) entre las dos estrellas en el cielo. Yo lo hago\(ω = 91^\circ .190 \ 79\).
Ahora que conocemos el ángulo entre las estrellas, podemos usar un triángulo plano para calcular la distancia entre ellas:
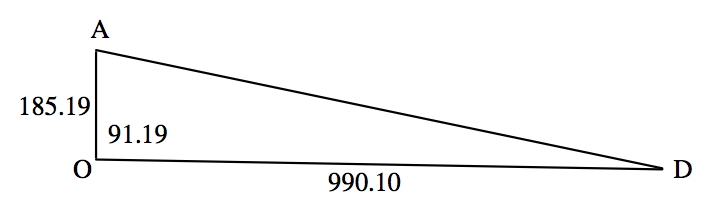
He marcado Antares (\(\text{A}\)), Deneb (\(\text{D}\)) y nosotros (\(\text{O}\)), y las distancias de nosotros a las dos estrellas, en pársecs. (Ese es el recíproco de sus paralaje en arcsec.) También he marcado los ángulos, en grados, entre Antares y Deneb. Ahora podemos usar la regla de coseno para planos triángulos, Ecuación 3.2.2, para encontrar la distancia\(\text{AD}\). Lo hago 1011 parsecs.
Un pársec es la distancia a la que una unidad astronómica (aproximadamente el radio de la órbita terrestre) subtendería un ángulo de un segundo de arco. Esto también significa, si llegas a pensarlo, que el número de unidades astronómicas en un pársec es igual al número de segundos de arco en un radián, que es\(360 \times 3600 \div (2π) = 2.062648 \times 10^5\). La distancia entre las estrellas es, por tanto, unidades\(1011 \times 2.062648 \times 10^5\) astronómicas. Multiplique esto por\(1.495 \ 98 \times 10^8\), para obtener la distancia en km. Hago la distancia\(3.120 \times 10^{16} \ \text{km}\).
Esto tardaría\(1.040596 \times 10^8\) segundos luz en viajar, o 3298 años, por lo que la distancia entre las estrellas es de 3298 años luz.
6.11.3
Veamos si podemos desarrollar una fórmula para un caso general. Haremos que el primer meteoro comience a las\((α_{11}, \ δ_{11})\) y termine a las\((α_{12}, \ δ_{12})\). El segundo meteoro comienza en\((α_{21}, \ δ_{21})\) y termina en\((α_{22}, \ δ_{22}\). Tenemos que encontrar las coordenadas\((α, \ δ\) del punto desde el que divergen los dos meteoros.
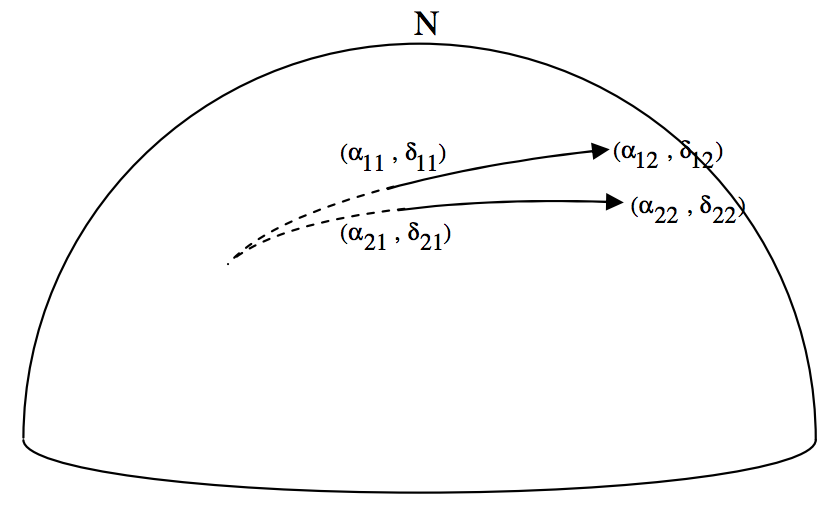
Este no es un problema particularmente fácil —pero es uno que obviamente es útil para los observadores de meteoritos. Simplemente esbozaré algunas sugerencias aquí, y dejaré al lector para que resuelva los detalles. Dibujaré debajo de uno de los meteoros, y el radiante, y el Polo Celestial Norte:
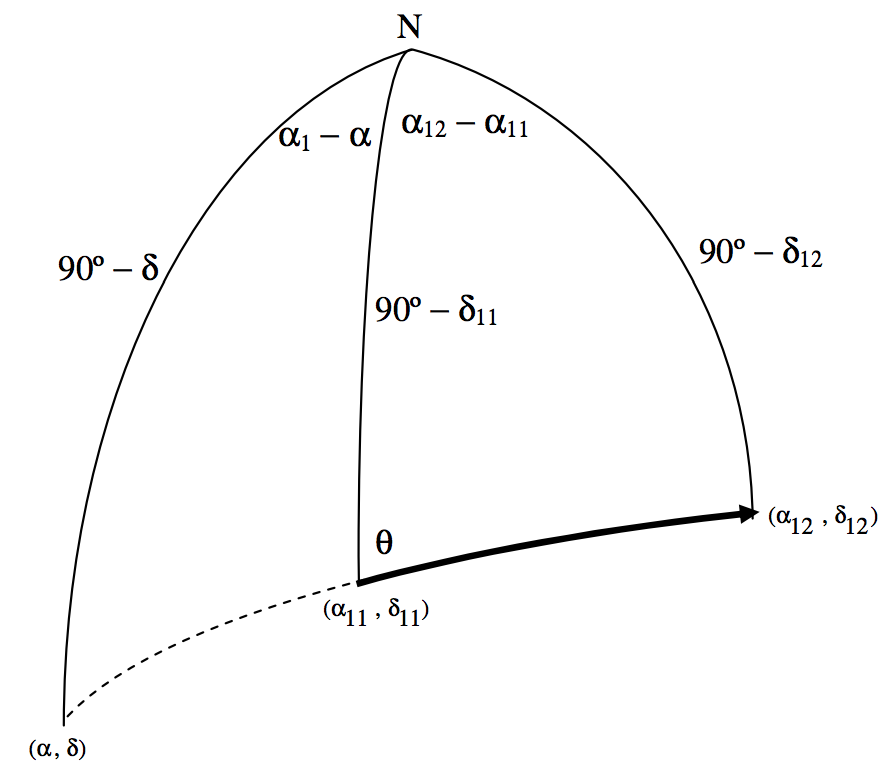
Usa la regla cotangente (Ecuación 3.5.5) en el triángulo derecho para obtener una expresión para\(\cot θ\):
\[\sin δ_{11} \cos (α_{12} - α_{11}) = \cos δ_{11} \tan δ_{12} + \sin (α_{12} - α_{11}) \cot θ.\]
Equiparar estas dos expresiones para\(\cot θ\) (es decir, eliminar\(θ\) entre las dos Ecuaciones). Esto te dará una sola Ecuación que contiene las dos incógnitas,\(α\) y\(δ\), siendo todo lo demás en la Ecuación una cantidad conocida. (Esto será obvio si en realidad estás haciendo un ejemplo numérico).
Ahora haz lo mismo para el segundo meteoro, y obtendrás una segunda Ecuación en α y δ. En principio ahora estás libre de casa, aunque puede haber un poco de álgebra pesada y trigonometría por recorrer antes de que finalmente llegues allí.
Hago la respuesta de la siguiente manera:
\[\tan α = \frac{\cos α_{22} \tan δ_{22} - \cos α_{12} \tan δ_{12} + a_1 \sin α_{12} - a_2 \sin α_{22}}{\sin α_{12} \tan δ_{12} - \sin α_{22} \tan δ_{22} + a_1 \cos α_{12} - a_2 \cos α_{22}},\]
donde\[a_1 = \frac{\tan δ_{11}}{\sin(α_{11} - α_{12})} - \frac{\tan δ_{12}}{\tan(α_{11} - α_{12})}\]
y\[a_2 = \frac{\tan δ_{21}}{\sin(α_{21} - α_{22})} - \frac{\tan δ_{22}}{\tan(α_{21} - α_{22})}\]
Entonces\[\tan δ = \cos (α - α_{12}) \tan δ_{12} + \sin (α - α_{12} ) [\csc (α_{11} - α_{12}) \tan δ_{11} - \cot (α_{11} - α_{12}) \tan δ_{12}]\]
o\[\tan δ = \cos (α - α_{22}) \tan δ_{22} + \sin (α - α_{22} ) [\csc (α_{21} - α_{22}) \tan δ_{21} - \cot (α_{21} - α_{22}) \tan δ_{22}].\]
Cualquiera de estas dos Ecuaciones para\(\tan δ\) debe dar el mismo resultado. En el programa informático que utilizo para este cálculo, lo consigo para calcular a\(\tan δ\) partir de ambas Ecuaciones, así como una comprobación de errores.
Esto puede parecer complicado, pero todos los términos son solo números calculables para cualquier caso en particular. Si el colure equinoccial se interpone en el camino (como lo hizo —deliberadamente— en el ejemplo numérico que di), sugiero solo agregar 24 horas a todas las ascensiones correctas.
Para el ejemplo numérico que di, hago que las coordenadas del radiante sean:
\[α = 22^\text{h} 01^\text{m}.3 \quad δ = - 00^\circ 37^\prime .\]