11.2: Coordenadas estándar y constantes de placa

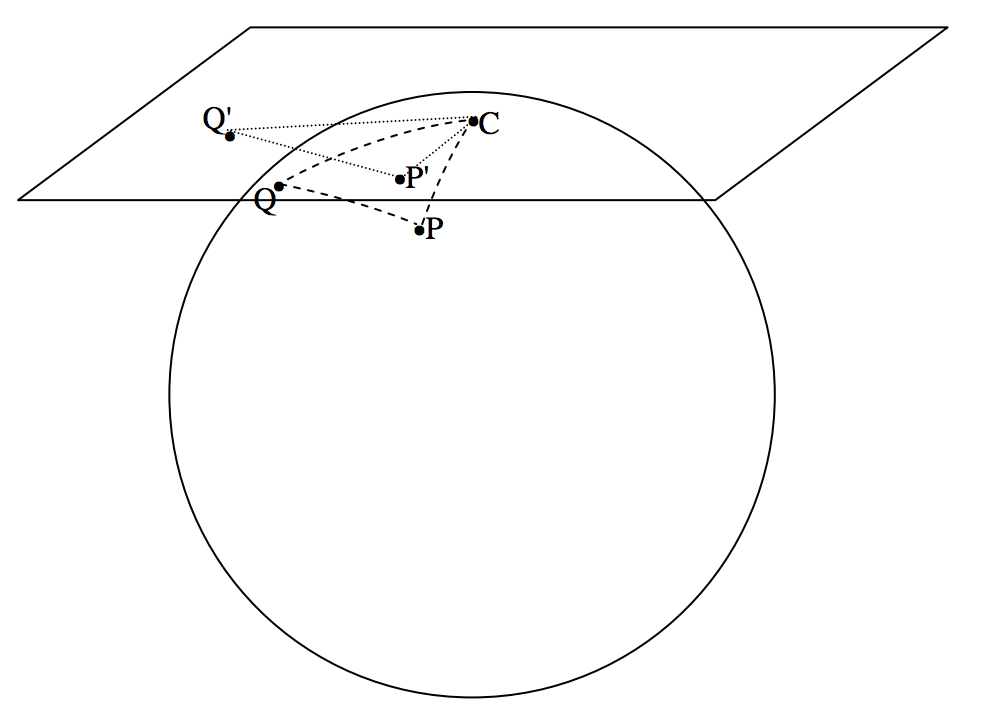
Supondremos que el eje óptico del telescopio, cuya distancia focal efectiva es\(F\), está apuntando a un punto de\(\text{C}\) la esfera celeste, cuya ascensión y declinación correctas son\((A, \ D)\). Las estrellas, como todo astrofísico sabe, están dispersas por la superficie de la esfera celeste, que es de radio arbitrario, y tomaré el radio para que sea igual a\(F\), la distancia focal del telescopio. En figura\(\text{XI.1}\), he dibujado el plano tangente al cielo en\(\text{C}\), que es lo que se registrará en la fotografía. En el plano tangente (que es similar al plano de la placa o película fotográfica) he dibujado dos ejes ortogonales:\(\text{C}ξ\) al este y\(\text{C}η\) al norte. He dibujado una estrella,\(\text{Q}\), cuyas coordenadas están\((α,δ)\), en la superficie de la esfera celeste, y su proyección,\(\text{Q}^\prime\), en el plano tangente, donde están sus coordenadas\((ξ , η)\). Cada estrella se mapea de manera similar en el plano tangente mediante una proyección similar. \((ξ , η)\)Las coordenadas se denominan coordenadas estándar de la estrella, y nuestra primera tarea es encontrar una relación entre las coordenadas ecuatoriales\((α,δ)\) en la superficie de la esfera celeste y las coordenadas estándar\((ξ , η)\) en el plano tangente o la fotografía.

En figura\(\text{XI.2}\), he vuelto a dibujar figura\(\text{XI.1}\), y, además de la estrella\(\text{Q}\) y su proyección\(\text{Q}^\prime\), también he dibujado el Polo Celestial norte\(\text{P}\) y su proyección\(\text{P}^\prime\). El punto\(\text{P}^\prime\) está en el\(η\) eje. El triángulo esférico se\(\text{PQC}\) mapea al triángulo plano\(\text{P}^\prime \text{Q}^\prime \text{C}\). En el triángulo esférico\(\text{PQC}\), el lado\(\text{PQ} = 90^\circ − δ\) y el lateral\(\text{PC} = 90^\circ − D\).

\(\text{FIGURE XI.1}\)

\(\text{FIGURE XI.1}\)

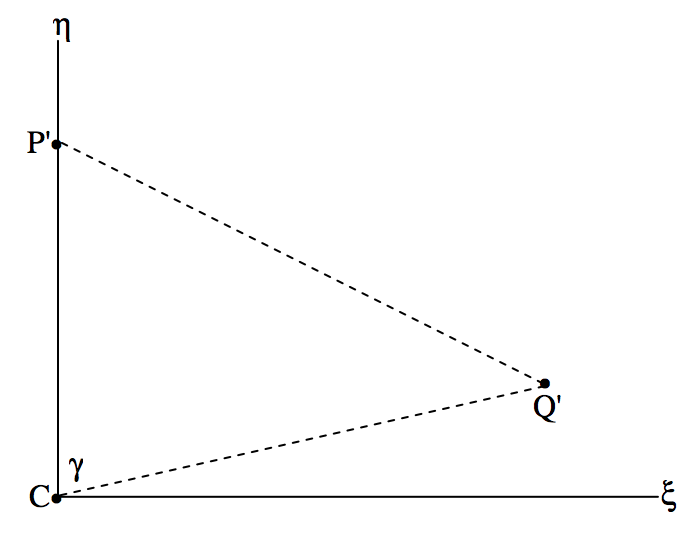
El ángulo\(\text{PCQ}\) en el triángulo esférico\(\text{PCQ}\) es igual al ángulo\(\text{P}^\prime \text{CQ}^\prime\) en el triángulo plano\(\text{P}^\prime \text{CQ}^\prime\), y llamaré a ese ángulo\(γ\). Voy a llamar al arco\(\text{CQ}\) en el triángulo esférico\(ε\). En la figura\(\text{XI.3}\) dibujo el plano tangente, mostrando los ejes\(ξ-\) y η-ejes y las proyecciones,\(\text{P}^\prime\) y\(\text{Q}^\prime\) del polo\(\text{P}\) y la estrella\(\text{Q}\), así como el triángulo plano\(\text{P}^\prime \text{CQ}^\prime\).

\(\text{FIGURE XI.3}\)

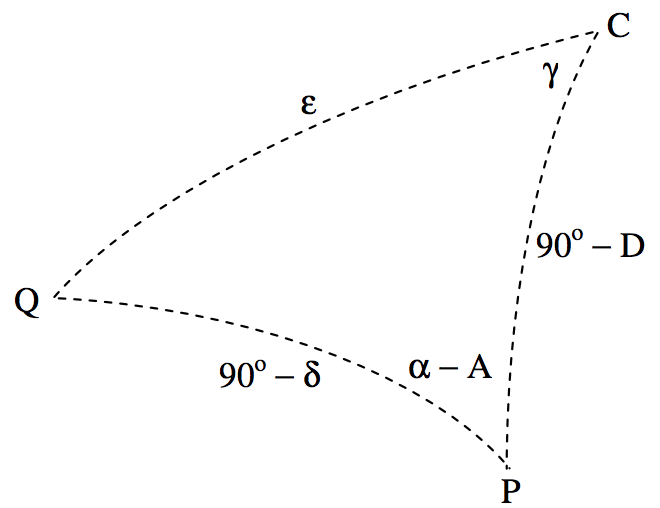
Las\(η\) coordenadas\(ξ\) y de\(\text{Q}^\prime\) son\((\text{CQ}^\prime \sin γ , \ \text{CQ}^\prime \cos γ)\). Y al mirar las cifras\(\text{XI.1}\) y\(\text{XI.2}\) por un tiempo, se puede ver eso\(\text{CQ}^\prime = F \tan ε\). Así son las coordenadas estándar de la imagen\(\text{Q}^\prime\) de la estrella en la fotografía, en unidades de la distancia focal del telescopio\((\tan ε \sin γ , \ \tan ε \cos γ )\). Queda ahora por encontrar expresiones para\(\tan ε \sin γ\) y\(\tan ε \cos γ\) en términos de las ascensiones y declinaciones correctas de\(\text{Q}\) y de\(\text{C}\). Dibujo ahora, en figura\(\text{XI.4}\), el triángulo esférico\(\text{PCQ}\).

\(\text{FIGURE XI.4}\)

Es fácil, a partir de las fórmulas habituales para triángulos esféricos, obtener expresiones para\(\cos ε\) y para\(\tan γ\):

\[\cos ε = \sin δ \sin D + \cos δ \cos D \cos (α - A) \label{11.2.1} \tag{11.2.1}\]

y

\[\tan γ = \frac{\sin (α - A)}{\cos D \tan δ - \sin D \cos (α - A)}, \label{11.2.2} \tag{11.2.2}\]

a partir del cual uno puede (eventualmente) calcular las coordenadas estándar\((ξ , η)\) de la estrella. También es posible calcular expresiones explícitas para\(\tan ε \sin γ\) y para\(\tan ε \cos γ\). Así, por otras aplicaciones de las fórmulas triangulares esféricas, tenemos

\[\tan ε = \frac{\cos D}{\sin D \cos γ + \cot (α - A) \sin γ}. \label{11.2.3} \tag{11.2.3}\]

Multiplicación de Ecuación\(\ref{11.2.3}\) por\(\sin γ\) da\(\tan ε \sin γ\) excepto que\(\tan γ\) aparece en el lado derecho. Esto, sin embargo, se puede eliminar mediante el uso de la Ecuación\ ref {11.2.2}, y se obtiene, después de algo de álgebra:

\[ξ = \tan ε \sin γ = \frac{\sin (α - A)}{\sin D \tan δ + \cos D \cos (α - A)}. \label{11.2.4} \tag{11.2.4}\]

De manera similar, puedes multiplicar Ecuación\(\text{11.2.3}\) por\(\cos γ\), y de nuevo eliminar\(\tan γ\) y eventualmente llegar a

\[η = \tan ε \cos γ = \frac{\tan δ - \tan D \cos (α - A)}{\tan D \tan δ + \cos(α - A)}. \label{11.2.5} \tag{11.2.5}\]

Estos dan las coordenadas estándar de una estrella o asteroide\((α , δ)\) en unidades de la distancia focal\(F\).

Ahora parecería que todo lo que tenemos que hacer es medir las coordenadas estándar\((ξ , η)\) de un objeto, e inmediatamente podemos determinar su ascensión y declinación correctas invirtiendo las Ecuaciones\ ref {11.2.4} y\ ref {11.2.5}:

\[\tan(α - A) = \frac{ξ}{\cos D - η \sin D} \label{11.2.6} \tag{11.2.6}\]

y

\[\tan δ = \frac{(η \cos D + \sin D)\sin(α - A)}{ξ}. \label{11.2.7} \tag{11.2.7}\]

Efectivamente, en principio eso es lo que tenemos que hacer —pero en la práctica todavía estamos a alguna manera de lograr nuestro objetivo.

Una pequeña dificultad es que desconocemos precisamente la distancia focal efectiva\(F\) (que depende de la temperatura). Un problema más grave es que desconocemos la posición exacta del centro de la placa, ni sabemos que las direcciones de desplazamiento de nuestro motor de medición de dos coordenadas son paralelas a las direcciones de ascensión y declinación correctas.

Lo mejor que podemos hacer es comenzar nuestras mediciones desde algún punto cerca del centro de la placa y medir (en mm más que en unidades de\(F\)) las distancias horizontal y vertical\((x , y)\) de las estrellas de comparación y el asteroide desde nuestro origen arbitrario. Estas\((x , y)\) coordenadas se denominan, naturalmente, las coordenadas medidas.

Las coordenadas medidas generalmente se expresarán en milímetros (o quizás en píxeles si se está utilizando un CCD), y la distancia lineal\(s\) entre dos imágenes estelares de comparación cualquiera se encuentra por el teorema de Pitágoras. La distancia angular\(ω\) entre dos estrellas cualquiera viene dada por la solución de un triángulo esférico como

\[\cos ω = \sin δ_1 \sin δ_2 + \cos δ_1 \cos δ_2 \cos (α_1 - α_2) \label{11.2.8} \tag{11.2.8}\]

La distancia focal\(F\) es entonces\(s/ω\), y esta puede calcularse para varios pares de estrellas y promediarse. A partir de ese punto, las coordenadas estándar se pueden expresar en unidades de\(F\).

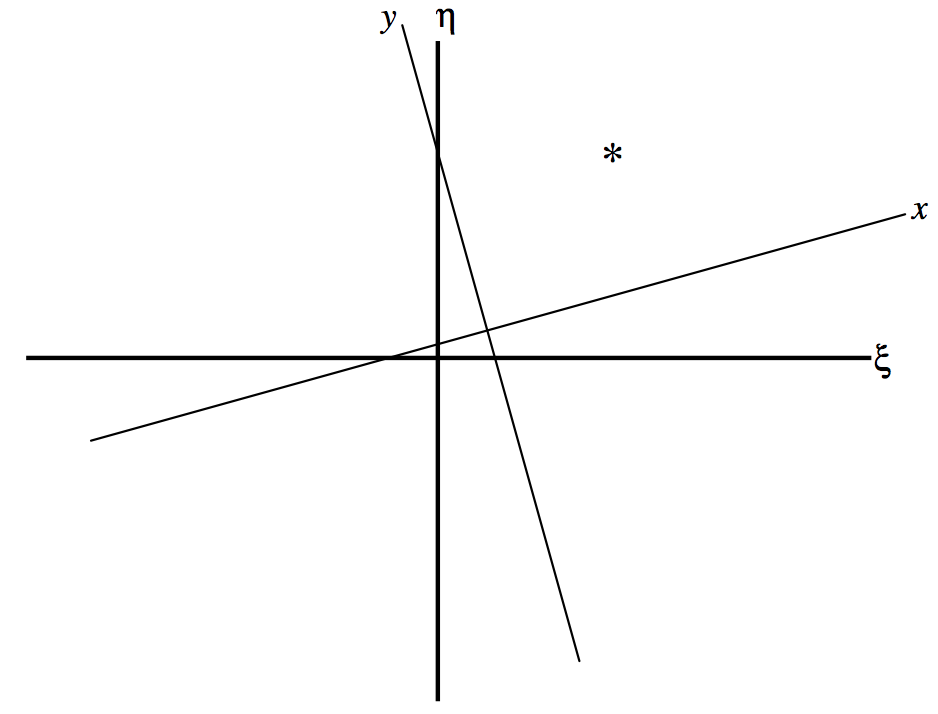
\((x , y)\)Las coordenadas medidas son desplazadas de las coordenadas estándar\((ξ , η)\) por una traslación desconocida y una rotación desconocida (figura\(\text{XI.4}\)), pero la relación entre ellas, si se desconoce, es al menos lineal (pero ver subsección\(\text{11.3.5}\)) y así de la forma:

\[ξ - x = ax + by + c, \label{11.2.9} \tag{11.2.9}\]

\[η - y = dx + ey + f . \label{11.2.10} \tag{11.2.10}\]

Las constantes\(a – f\) son las constantes de placa. Se determinan midiendo las coordenadas estándar para un mínimo de tres estrellas de comparación cuyas ascensiones y declinaciones correctas son conocidas y para las cuales, por lo tanto, se pueden calcular las coordenadas estándar. Tres conjuntos de Ecuaciones\ ref {11.2.9} y 10 pueden entonces ser establecidos y resueltos para las constantes de placa. En la práctica se deben elegir más de tres estrellas de comparación, y se debe determinar una solución de mínimos cuadrados. Para saber cómo hacerlo, véase la sección 8 del capítulo 1, o el artículo citado en la fracción 1 de este capítulo. En los días fotográficos, solo se utilizaron unas pocas (quizás media docena) de estrellas de comparación. Hoy en día, cuando hay catálogos que contienen cientos de millones de estrellas, y la\(\text{CCD}\) medición y el cálculo automático son mucho más rápidos, se pueden usar varias docenas de estrellas de comparación, y cualquier medición deficiente (o posiciones deficientes del catálogo) puede identificarse y rechazarse rápidamente.

Habiendo determinado las constantes de placa, las Ecuaciones\ ref {11.2.9} y 10 pueden ser utilizadas para calcular las coordenadas estándar del asteroide, y de ahí su ascensión y declinación correctas se pueden calcular a partir de las Ecuaciones\ ref {11.2.6} y 7.

\(\text{FIGURE 11.5}\)

Cabe señalar que la posición del asteroide que has medido —y debes reportar al Centro del Planeta Menor, es la posición topocéntrica (es decir, medida desde tu posición sobre la superficie de la Tierra) más que la posición geocéntrica (vista desde el centro de la Tierra). El Centro Planeta Menor espera recibir del observador la posición topocéntrica; el MPC sabrá hacer la corrección al centro de la Tierra.