2.10: Separación Variable — Coordenadas cilíndricas

Ahora, discutamos si es posible generalizar nuestro acercamiento a problemas cuya geometría sigue siendo axialmente simétrica, pero con una dependencia sustancial del potencial de la coordenada axial (\(\ \partial \phi / \partial z \neq 0\)). El ejemplo clásico de tal problema se muestra en la Fig. 17. Aquí la pared lateral y la tapa inferior de un cilindro redondo hueco se mantienen a un potencial fijo (digamos,\(\ \phi=0\)), pero el potencial\(\ V\) fijado en la tapa superior es diferente. Evidentemente, este problema es cualitativamente similar al problema de caja rectangular resuelto anteriormente (Fig. 13), y también intentaremos resolverlo primero para el caso de distribución arbitraria de voltaje sobre la tapa superior:\(\ V=V(\rho, \varphi)\).

Fig. 2.17. Un volumen cilíndrico con paredes conductoras.

Siguiendo la idea principal del método de separación de variables, requerimos que cada función parcial\(\ \phi_{k}\) en la ecuación (84) satisfaga la ecuación de Laplace, ahora en las coordenadas cilíndricas completas\(\ \{\rho, \varphi, z\}\): ³⁹

\[\ \frac{1}{\rho} \frac{\partial}{\partial \rho}\left(\rho \frac{\partial \phi_{k}}{\partial \rho}\right)+\frac{1}{\rho^{2}} \frac{\partial^{2} \phi_{k}}{\partial \varphi^{2}}+\frac{\partial^{2} \phi_{k}}{\partial z^{2}}=0.\tag{2.124}\]

Conectando\(\ \phi_{k}\) en la forma del producto\(\ \mathcal{R}(\rho) \mathcal{F}(\varphi) \mathcal{Z}(z)\) en la Eq. (124) y dividiendo todos los términos resultantes por\(\ \mathcal{RFZ}\), obtenemos

\[\ \frac{1}{\rho \mathcal{R}} \frac{d}{d \rho}\left(\rho \frac{d \mathcal{R}}{d \rho}\right)+\frac{1}{\rho^{2} \mathcal{F}} \frac{d^{2} \mathcal{F}}{d \varphi^{2}}+\frac{1}{\mathcal{Z}} \frac{d^{2} \mathcal{Z}}{d z^{2}}=0.\tag{2.125}\]

Ya que los dos primeros términos de la Ec. (125) sólo pueden depender de las variables polares\(\ \rho\) y\(\ \varphi\), mientras que el tercer término, sólo en\(\ z\), al menos ese término debe ser igual a una constante. Denotándolo (al igual que en el problema de la caja rectangular) por\(\ \gamma^{2}\), obtenemos el siguiente conjunto de dos ecuaciones:

\[\ \frac{d^{2} \mathcal{Z}}{d z^{2}}=\gamma^{2} z,\tag{2.126}\]

\[\ \frac{1}{\rho \mathcal{R}} \frac{d}{d \rho}\left(\rho \frac{d \mathcal{R}}{d \rho}\right)+\gamma^{2}+\frac{1}{\rho^{2} \mathcal{F}} \frac{d^{2} \mathcal{F}}{d \varphi^{2}}=0.\tag{2.127}\]

Ahora bien, multiplicando todos los términos de la Ec. (127) por\(\ \rho^{2}\), vemos que el último término del resultado,\(\ \left(d^{2} \mathcal{F} /d \varphi^{2}\right) / \mathcal{F}\), puede depender sólo de\(\ \varphi\), y así debe ser constante. Llamando a esa constante\(\ v^{2}\) (al igual que en la Sec. 6 anterior), separamos la ecuación (127) en una ecuación angular,

\[\ \frac{d^{2} \mathcal{F}}{d \varphi^{2}}+v^{2} \mathcal{F}=0,\tag{2.128}\]

y una ecuación radial:

\[\ \frac{d^{2} \mathcal{R}}{d \rho^{2}}+\frac{1}{\rho} \frac{d \mathcal{R}}{d \rho}+\left(\gamma^{2}-\frac{v^{2}}{\rho^{2}}\right) \mathcal{R}=0.\tag{2.129}\]

Vemos que las ecuaciones diferenciales ordinarias para las funciones\(\ \mathcal{Z}(z)\) y\(\ \mathcal{F}(\varphi)\) (y de ahí sus soluciones) son idénticas a las discutidas anteriormente en este capítulo. Sin embargo, la ecuación (129) para la función radial\(\ \mathcal{R}(\rho)\) (llamada ecuación de Bessel) es más compleja que en el caso 2D, y depende de dos parámetros constantes
independientes,\(\ \gamma\) y\(\ v\). Este último desafío puede superarse fácilmente si observamos que cualquier cambio de\(\ \gamma\) puede reducirse al reescalado correspondiente de la coordenada radial\(\ \rho\). De hecho, la introducción de una variable adimensional\(\ \xi \equiv \gamma \rho\), ⁴⁰ Eq. (129) puede reducirse a una ecuación con solo un parámetro,\(\ v\).

Ecuación de Bessel

\[\ \frac{d^{2} \mathcal{R}}{d \xi^{2}}+\frac{1}{\xi} \frac{d \mathcal{R}}{d \xi}+\left(1-\frac{v^{2}}{\xi^{2}}\right) \mathcal{R}=0.\tag{2.130}\]

Además, ya sabemos que para problemas ángulo-periódicos, el espectro de valores propios de la Ec. (128) es discreto:\(\ v=n\), con entero\(\ n\).

Desafortunadamente, incluso en este caso, la ecuación (130), que es la forma canónica de la ecuación de Bessel, no puede satisfacerse con una sola función “elemental”. Sus soluciones que necesitamos para nuestro problema actual se llaman la función Bessel del primer tipo, de orden\(\ v\), comúnmente denotada como\(\ J_v(\xi)\). Permítanme revisar brevemente aquellas propiedades de estas funciones que son más relevantes para nuestro problema, y muchos otros problemas discutidos en esta serie. ⁴¹

En primer lugar, la función Bessel de un orden entero negativo se relaciona muy simplemente con eso con el orden positivo:

\[\ J_{-n}(\xi)=(-1)^{n} J_{n}(\xi),\tag{2.131}\]

permitiéndonos limitar nuestra discusión a las funciones con\(\ n \geq 0\). La Figura 18 muestra cuatro de estas funciones con el menor positivo\(\ n\).

Fig. 2.18. Varias funciones\(\ J_{n}(\xi)\) de Bessel de orden entero. Las líneas discontinuas muestran la envolvente de las asíntotas (135).

A medida que se incrementa su argumento, cada función está inicialmente cerca de una ley de poder:\(\ J_{0}(\xi) \approx 1\)\(\ J_{1}(\xi) \approx \xi / 2=\xi/2\),\(\ J_{2}(\xi) \approx \xi^{2} / 8\),, etc. Este comportamiento se desprende de la serie Taylor

\[\ J_{n}(\xi)=\left(\frac{\xi}{2}\right)^{n} \sum_{k=0}^{\infty} \frac{(-1)^{k}}{k !(n+k) !}\left(\frac{\xi}{2}\right)^{2 k},\tag{2.132}\]

que es formalmente válido para cualquiera\(\ \xi\), e incluso puede servir como una definición alternativa de las funciones\(\ J_{n}(\xi)\). Sin embargo, la serie está convergiendo rápidamente solo a pequeños argumentos,\(\ \xi<n\), donde su término principal es

\[\ \left.J_{n}(\xi)\right|_{\xi \rightarrow 0} \rightarrow \frac{1}{n !}\left(\frac{\xi}{2}\right)^{n}.\tag{2.133}\]

At\(\ \xi \approx n+1.86 n^{1 / 3}\), la función Bessel alcanza su máximo ⁴²

\[\ \max _{\xi}\left[J_{n}(\xi)\right] \approx \frac{0.675}{n^{1 / 3}},\tag{2.134}\]

y luego comienza a oscilar con un periodo que se aproxima gradualmente a 2\(\ \pi\), un desplazamiento de fase que aumenta\(\ \pi / 2\) con cada unidad de incremento de\(\ n\), y una amplitud que disminuye como\(\ \xi^{1 / 2}\). Todas estas características se describen mediante la siguiente fórmula asintótica:

\[\ \left.J_{n}(\xi)\right|_{\xi \rightarrow \infty} \rightarrow\left(\frac{2}{\pi \xi}\right)^{1 / 2} \cos \left(\xi-\frac{\pi}{4}-\frac{n \pi}{2}\right),\tag{2.135}\]

que comienza a dar una aproximación razonable muy poco después de que la función alcanza los picos máximos — ver Fig. 18. ⁴³

Ahora estamos listos para nuestro estudio de caso (Fig. 17). Seleccionemos las funciones\(\ \mathcal{Z}(z)\) para que satisfagan la Ec. (126) y la condición de límite de tapa inferior\(\ \mathcal{Z}(0)=0\), es decir, son proporcionales a\(\ \sinh \gamma z\) — cf. Ec. (94). Entonces obtenemos

\[\ \phi=\sum_{n=0}^{\infty} \sum_{\gamma} J_{n}(\gamma \rho)\left(c_{n \gamma} \cos n \varphi+s_{n \gamma} \sin n \varphi\right) \sinh \gamma z.\tag{2.136}\]

A continuación, necesitamos satisfacer la condición de límite cero en la pared lateral del cilindro\(\ (\rho=R)\). Esto puede garantizarse tomando

\[\ J_{n}(\gamma R)=0.\tag{2.137}\]

Dado que cada función\(\ J_{n}(x)\) tiene un número infinito de ceros positivos (ver nuevamente la Fig. 18), que pueden ser numerados por un índice entero\(\ m=1,2, \ldots\), la ecuación (137) puede satisfacerse con un número infinito de valores discretos del parámetro de separación\(\ \gamma\).

\[\ \gamma_{n m}=\frac{\xi_{n m}}{R},\tag{2.138}\]

donde\(\ \xi_{n m}\) es el\(\ m\) -ésimo cero de la función\(\ J_{n}(x)\) — ver los números superiores en las celdas de la Tabla 1. (Muy pronto veremos para qué necesitamos los números inferiores.)

Cuadro 2.1. Valores aproximados de unos pocos primeros ceros,\(\ \xi_{n m}\), de algunas funciones de Bessel de orden inferior\(\ J_{n}(\xi)\) (el número superior en cada celda), y los valores de\(\ d J_{n}(\xi) / d \xi\) en estos puntos (el número inferior).

	\(\ m = 1\)	2	3	4	5	6
\(\ n = 0\)	2.40482 -0.51914	5.52008 +0.34026	8.65372 -0.27145	11.79215 +0.23245	14.93091 -0.20654	18.07106 +0.18773
1	3.83171 -0.40276	7.01559 +0.30012	10.17347 -0.24970	13.32369 +0.21836	16.47063 -0.19647	19.61586 +0.18006
2	5.13562 -0.33967	8.41724 +0.27138	11.61984 -0.23244	14.79595 +0.20654	17.95982 -0.18773	21.11700 +0.17326
3	6.38016 -0.29827	9.76102 +0.24942	13.01520 -0.21828	16.22347 +0.19644	19.40942 -0.18005	22.58273 +0.16718
4	7.58834 -0.26836	11.06471 +0.23188	14.37254 -0.20636	17.61597 +0.18766	20.82693 -0.17323	24.01902 +0.16168
5	8.77148 -0.24543	12.33860 +0.21743	15.70017 -0.19615	18.98013 +0.17993	22.21780 -0.16712	25.43034 +0.15669

Por lo tanto, la Ec. (136) puede representarse en una forma más explícita:

Separación variable en coordenadas cilíndricas (ejemplo)

\[\ \phi(\rho, \varphi, z)=\sum_{n=0}^{\infty} \sum_{m=1}^{\infty} J_{n}\left(\xi_{n m} \frac{\rho}{R}\right)\left(c_{n m} \cos n \varphi+s_{n m} \sin n \varphi\right) \sinh \left(\xi_{n m} \frac{z}{R}\right).\tag{2.139}\]

Aquí los coeficientes\(\ c_{n m}\) y\(\ s_{n m}\) tienen que ser seleccionados para satisfacer la única condición de límite restante — que en la tapa superior:

\[\ \phi(\rho, \varphi, l) \equiv \sum_{n=0}^{\infty} \sum_{m=1}^{\infty} J_{n}\left(\xi_{n m} \frac{\rho}{R}\right)\left(c_{n m} \cos n \varphi+s_{n m} \sin n \varphi\right) \sinh \left(\xi_{n m} \frac{l}{R}\right)=V(\rho, \varphi).\tag{2.140}\]

Para usarlo, multipliquemos ambas partes de la ecuación (140) por\(\ J_{n}\left(\xi_{n m^{\prime}} \rho / R\right) \cos n^{\prime} \varphi\), integremos el resultado sobre el área de la tapa y utilicemos la siguiente propiedad de las funciones de Bessel:

\[\ \int_{0}^{1} J_{n}\left(\xi_{n m} s\right) J_{n}\left(\xi_{n m^{\prime}} s\right) s d s=\frac{1}{2}\left[J_{n+1}\left(\xi_{n m}\right)\right]^{2} \delta_{m m^{\prime}}.\tag{2.141}\]

La última relación expresa una ortogonalidad muy específica (“2D”) de las funciones de Bessel con diferentes índices\(\ m\) no las confundas con las órdenes de función\(\ n\), ¡por favor! ⁴⁴ Dado que relaciona dos funciones de Bessel del mismo orden\(\ n\), es natural preguntarse por qué su lado derecho contiene la función con un orden diferente\(\ (n+1)\). Algunos instintos de eso pueden provenir de una propiedad más muy importante de las funciones de Bessel, las llamadas relaciones de recurrencia: ⁴⁵

\[\ J_{n-1}(\xi)+J_{n+1}(\xi)=\frac{2 n J_{n}(\xi)}{\xi},\tag{2.142a}\]

\[\ J_{n-1}(\xi)-J_{n+1}(\xi)=2 \frac{d J_{n}(\xi)}{d \xi},\tag{2.142b}\]

que en particular producen la siguiente fórmula (conveniente para elaborar algunas integrales de la función de Bessel):

\[\ \frac{d}{d \xi}\left[\xi^{n} J_{n}(\xi)\right]=\xi^{n} J_{n-1}(\xi).\tag{2.143}\]

Para nuestros propósitos actuales, apliquemos las relaciones de recurrencia en los puntos especiales\(\ \xi_{n m}\). En estos puntos, se\(\ J_{n}\) desvanece, y el sistema de dos ecuaciones (142) puede resolverse fácilmente para obtener, en particular,

\[\ J_{n+1}\left(\xi_{n m}\right)=-\frac{d J_{n}}{d \xi}\left(\xi_{n m}\right),\tag{2.144}\]

de manera que el corchete en el lado derecho de la Eq. (141) está justo\(\ \left(d J_{n} / d \xi\right)^{2}\) en\(\ \xi=\xi_{n m}\). Así, los valores de las derivadas de la función de Bessel en los puntos cero de la función, dados por los números más bajos en las celdas del Cuadro 1, son tan importantes para las soluciones de problemas de límite como los propios ceros.

Dado que las funciones angulares también\(\ \cos n \varphi\) son ortogonales, ambas entre sí,

\[\ \int_{0}^{2 \pi} \cos (n \varphi) \cos \left(n^{\prime} \varphi\right) d \varphi=\pi \delta_{n n^{\prime}},\tag{2.145}\]

y a todas las funciones\(\ \sin n \varphi\), la integración sobre el área de la tapa mata todos los términos de ambas series en la Ec. (140), además de solo un término proporcional a\(\ c_{n^{\prime} m^{\prime}}\), y por lo tanto da una expresión explícita para ese coeficiente. Los coeficientes de contrapartida se\(\ s_{n^{\prime} m^{\prime}}\) pueden encontrar repitiendo el mismo procedimiento con la sustitución de\(\ \cos n^{\prime} \varphi\) por\(\ \sin n^{\prime} \varphi\). Esta evaluación (dejada para el ejercicio del lector) completa la solución de nuestro problema para un potencial de tapa arbitraria\(\ V(\rho, \varphi)\).

Aún así, antes de dejar las funciones de Bessel (solo por un tiempo: -), necesitamos abordar dos temas importantes. Primero, hemos visto que en nuestro problema de cilindro (Fig. 17), el conjunto de funciones\(\ J_{n}\left(\xi_{n m} \rho / R\right)\) con diferentes índices\(\ m\) (que caracterizan el grado de estiramiento de la función de Bessel a lo largo del eje\(\ \rho\)) juega un papel
similar al de las funciones\(\ \sin (\pi n x / a)\) en el problema de la caja rectangular mostrado en la Fig. 13. En este contexto, ¿cuál es el análogo de funciones\(\ \cos (\pi n x / a)\) —que puede ser importante para algunos problemas de límites? En un lenguaje más formal, ¿hay alguna función del mismo argumento\(\ \xi \equiv \xi_{n m} \rho / R\), que sería linealmente independiente de las funciones de Bessel de primer tipo, a la vez que satisfacía la misma ecuación de Bessel (130)?

La respuesta es sí. Para la definición de tales funciones, primero necesitamos generalizar nuestras fórmulas anteriores para\(\ J_{n}(\xi)\), y en particular la ecuación (132), al caso del orden arbitrario, no necesariamente real\(\ v\). Matemáticas dice que la generalización se puede realizar de la siguiente manera:

\[\ J_{v}(\xi)=\left(\frac{\xi}{2}\right)^{v} \sum_{k=0}^{\infty} \frac{(-1)^{k}}{k ! \Gamma(v+k+1)}\left(\frac{\xi}{2}\right)^{2 k},\tag{2.146}\]

donde\(\ \Gamma(s)\) está la llamada función gamma que puede definirse como ⁴⁶

\[\ \Gamma(s) \equiv \int_{0}^{\infty} \xi^{s-1} e^{-\xi} d \xi.\tag{2.147}\]

La propiedad más simple, y la más importante de la función gamma es que para los valores enteros de su argumento, da el factorial del número menor por uno:

\[\ \Gamma(n+1)=n ! \equiv 1 \cdot 2 \cdot \ldots \cdot n,\tag{2.148}\]

por lo que es esencialmente una generalización de la noción de lo factorial a todos los números reales.

Las funciones de Bessel definidas por la Ec. (146) satisfacen, después de los reemplazos\(\ n \rightarrow v\) y\(\ n ! \rightarrow \Gamma(n+1)\), prácticamente todas las relaciones discutidas anteriormente, incluyendo la ecuación de Bessel (130), la fórmula asintótica (135), la condición de ortogonalidad (141) y las relaciones de recurrencia (142). Además, se puede demostrar que\(\ v \neq n\), las funciones\(\ J_{v}(\xi)\) y\(\ J_{-v}(\xi)\) son linealmente independientes entre sí, y por lo tanto su combinación lineal puede ser utilizada para representar la solución general de la ecuación de Bessel. Desafortunadamente, como muestra la Ec. (131), pues\(\ v=n\) esto no es cierto, y una solución linealmente independiente de\(\ J_{n}(\xi)\) tiene que formarse de manera diferente. La forma más común de hacerlo es primero definir, para todos\(\ v \neq n\), las siguientes funciones:

\[\ Y_{v}(\xi) \equiv \frac{J_{v}(\xi) \cos v \pi-J_{-v}(\xi)}{\sin v \pi},\tag{2.149}\]

llamado las funciones de Bessel del segundo tipo, o más a menudo las funciones Weber, ⁴⁷ y luego seguir el límite\(\ v \rightarrow n\). En esto, tanto el numerador como el denominador del lado derecho de la ecuación (149) tienden a cero, pero su relación tiende a un valor finito llamado\(\ Y_{n}(x)\). Se puede demostrar que las funciones resultantes
siguen siendo las soluciones de la ecuación de Bessel y son linealmente independientes de\(\ J_{n}(x)\), aunque están relacionadas igual que esas funciones si el signo de\(\ n\) cambios:

\[\ Y_{-n}(\xi)=(-1)^{n} Y_{n}(\xi).\tag{2.150}\]

La Figura 19 muestra algunas funciones Weber de los órdenes enteros más bajos.

Fig. 2.19. Algunas funciones de Bessel de segundo tipo (también conocidas como las funciones Weber, también conocidas como las funciones Neumann).

Las parcelas muestran que el comportamiento asintótico es muy similar al de\(\ J_{n}(\xi)\),

\[\ Y_{n}(\xi) \rightarrow\left(\frac{2}{\pi \xi}\right)^{1 / 2} \sin \left(\xi-\frac{\pi}{4}-\frac{n \pi}{2}\right), \quad \text { for } \xi \rightarrow \infty,\tag{2.151}\]

pero con el desplazamiento de fase necesario para hacer estas funciones de Bessel ortogonales a las del orden puño — cf. Ec. (135). Sin embargo, para pequeños valores de argumento\(\ \xi\), las funciones de Bessel del segundo tipo se comportan de manera completamente diferente a las del primer tipo:

\[\ Y_{n}(\xi) \rightarrow \begin{cases}\frac{2}{\pi}\left(\ln \frac{\xi}{2}+\gamma\right), & \text { for } n=0, \\ -\frac{(n-1) !}{\pi}\left(\frac{\xi}{2}\right)^{-n}, & \text { for } n \neq 0,\end{cases}\tag{2.152}\]

donde\(\ \gamma\) se encuentra la llamada constante de Euler, definida de la siguiente manera:

\[\ \gamma \equiv \lim _{n \rightarrow \infty}\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}-\ln n\right) \approx 0.577157 \ldots\tag{2.153}\]

Como muestran las ecuaciones (152) y la Fig. 19, las funciones\(\ Y_{n}(\xi)\) divergen en\(\ \xi \rightarrow 0\) y por lo tanto no pueden describir el comportamiento de ninguna variable física, en particular el potencial electrostático.

Uno puede preguntarse: si esto es cierto, ¿cuándo necesitamos estas funciones en la física? La Figura 20 muestra un ejemplo de un problema de límite simple de la electrostática, cuya solución por el método de separación variable implica\(\ J_{n}(\xi)\) tanto funciones como\(\ Y_{n}(\xi)\).

Fig. 2.20. Un simple problema de límites que no se puede resolver usando solo un tipo de funciones de Bessel.

Aquí dos tubos cilíndricos coaxiales conductores redondos se mantienen al mismo (digamos, cero) potencial, pero al menos una de las dos tapas tiene un potencial diferente. El problema es casi completamente similar al discutido anteriormente (Fig. 17), pero ahora necesitamos encontrar la distribución potencial en el espacio libre entre los tubos, es decir, para\(\ R_{1}<\rho<R_{2}\). Si usamos la misma separación de variables que en el problema de contraparte más simple, necesitamos que las funciones\(\ \mathcal{R}(\rho)\) radiales satisfagan dos condiciones de límite cero: at\(\ \rho=R_{1}\) y\(\ \rho=R_2\). Con las funciones de Bessel de solo el primer tipo,\(\ J_{n}(\gamma \rho)\), es imposible de hacer, porque los dos límites impondrían dos condiciones independientes (y generalmente incompatibles),\(\ J_{n}\left(\gamma R_{1}\right)=0\), y\(\ J_{n}\left(\gamma R_{2}\right)=0\), sobre un “parámetro de estiramiento”\(\ \gamma\). La existencia de las funciones Bessel de segundo tipo salva inmediatamente el día, ya que si la solución de función radial se representa como una combinación lineal,

\[\ \mathcal{R}=c_{J} J_{n}(\gamma \rho)+c_{Y} Y_{n}(\gamma \rho),\tag{2.154}\]

dos condiciones de límite cero dan dos ecuaciones para\(\ \gamma\) y la relación\(\ c \equiv c_{Y} / c_{J}\). ⁴⁸ (Debido al carácter oscilante de ambas funciones de Bessel, estas condiciones normalmente serían satisfechas por un conjunto infinito de pares discretos)\(\ \{\gamma, c\}\). Obsérvese, sin embargo, que generalmente ninguno de estos pares correspondería a ceros de
cualquiera\(\ J_{n}\) o\(\ Y_{n}\), por lo que tener un análogo de la Tabla 1 para esta última función no ayudaría mucho. De ahí que incluso los problemas más simples de este tipo (como el que se muestra en la Fig. 20) típicamente requieren la solución numérica de ecuaciones algebraicas trascendentales.

Para completar la discusión de la separación de variables en las coordenadas cilíndricas, un tema más a abordar son las llamadas funciones de Bessel modificadas: de primer tipo\(\ I_{\nu}(\xi)\),, y de segundo tipo,\(\ K_{\nu}(\xi)\). Son dos soluciones linealmente independientes de la ecuación de Bessel modificada,

Ecuación de Bessel modificada

\[\ \frac{d^{2} \mathcal{R}}{d \xi^{2}}+\frac{1}{\xi} \frac{d \mathcal{R}}{d \xi}-\left(1+\frac{\nu^{2}}{\xi^{2}}\right) \mathcal{R}=0,\tag{2.155}\]

que difiere de la ecuación (130) “sólo” por el signo de uno de sus términos. La Figura 21 muestra un problema simple que conduce (entre muchos otros) a esta ecuación: se corta una tubería cilíndrica conductora delgada redonda, perpendicular a su eje, a anillos de igual altura h, que se mantienen a potenciales iguales pero alternos de signo.

Fig. 2.21. Un problema típico de límites cuya solución puede describirse convenientemente en términos de las funciones modificadas de Bessel.

Si el sistema es muy largo (formalmente, infinito) en la dirección z, podemos usar el método de separación variable para la solución a este problema, pero ahora evidentemente necesitamos soluciones periódicas (en lugar de exponenciales) a lo largo del eje z, es decir, combinaciones lineales de\(\ \sin k z\) y\(\ \cos k z\) con varios valores reales de la constante\(\ k\). Separando las variables, llegamos a una ecuación diferencial similar a la Ec. (129), pero con el signo negativo antes de la constante de separación:

\[\ \frac{d^{2} \mathcal{R}}{d \rho^{2}}+\frac{1}{\rho} \frac{d \mathcal{R}}{d \rho}-\left(k^{2}+\frac{\nu^{2}}{\rho^{2}}\right) \mathcal{R}=0.\tag{2.156}\]

La normalización de la misma coordenada radial,\(\ \xi \equiv k \rho\), inmediatamente nos lleva a la Eq. (155), y por lo tanto (for\(\ \nu=n\)) a las funciones modificadas de Bessel\(\ I_{n}(\xi)\) y\(\ K_{n}(\xi)\).

La Figura 22 muestra el comportamiento de tales funciones, de unos pocos órdenes más bajos. Se puede ver que en\(\ \xi \rightarrow 0\) el comportamiento es prácticamente similar al de las funciones “habituales” de Bessel — cf. Eqs. (132) y (152), con\(\ K_{n}(\xi)\) multiplicado (por razones puramente históricas) por un coeficiente adicional,\(\ \pi / 2\):

\[\ I_{n}(\xi) \rightarrow \frac{1}{n !}\left(\frac{\xi}{2}\right)^{n}, \quad K_{n}(\xi) \rightarrow \begin{cases}-\left[\ln \left(\frac{\xi}{2}\right)+\gamma\right], & \text { for } n=0, \\ \frac{(n-1) !}{2}\left(\frac{\xi}{2}\right)^{-n}, & \text { for } n \neq 0,\end{cases}\tag{2.157}\]

Sin embargo, el comportamiento asintótico de las funciones modificadas es muy diferente, con un crecimiento\(\ I_{n}(x)\) exponencial y una caída\(\ K_{n}(\xi)\) exponencial en\(\ \xi \rightarrow \infty\):

\[\ I_{n}(\xi) \rightarrow\left(\frac{1}{2 \pi \xi}\right)^{1 / 2} e^{\xi}, \quad K_{n}(\xi) \rightarrow\left(\frac{\pi}{2 \xi}\right)^{1 / 2} e^{-\xi}.\tag{2.158}\]

Fig. 2.22. Las funciones Bessel modificadas del primer tipo (panel izquierdo) y del segundo tipo (panel derecho).

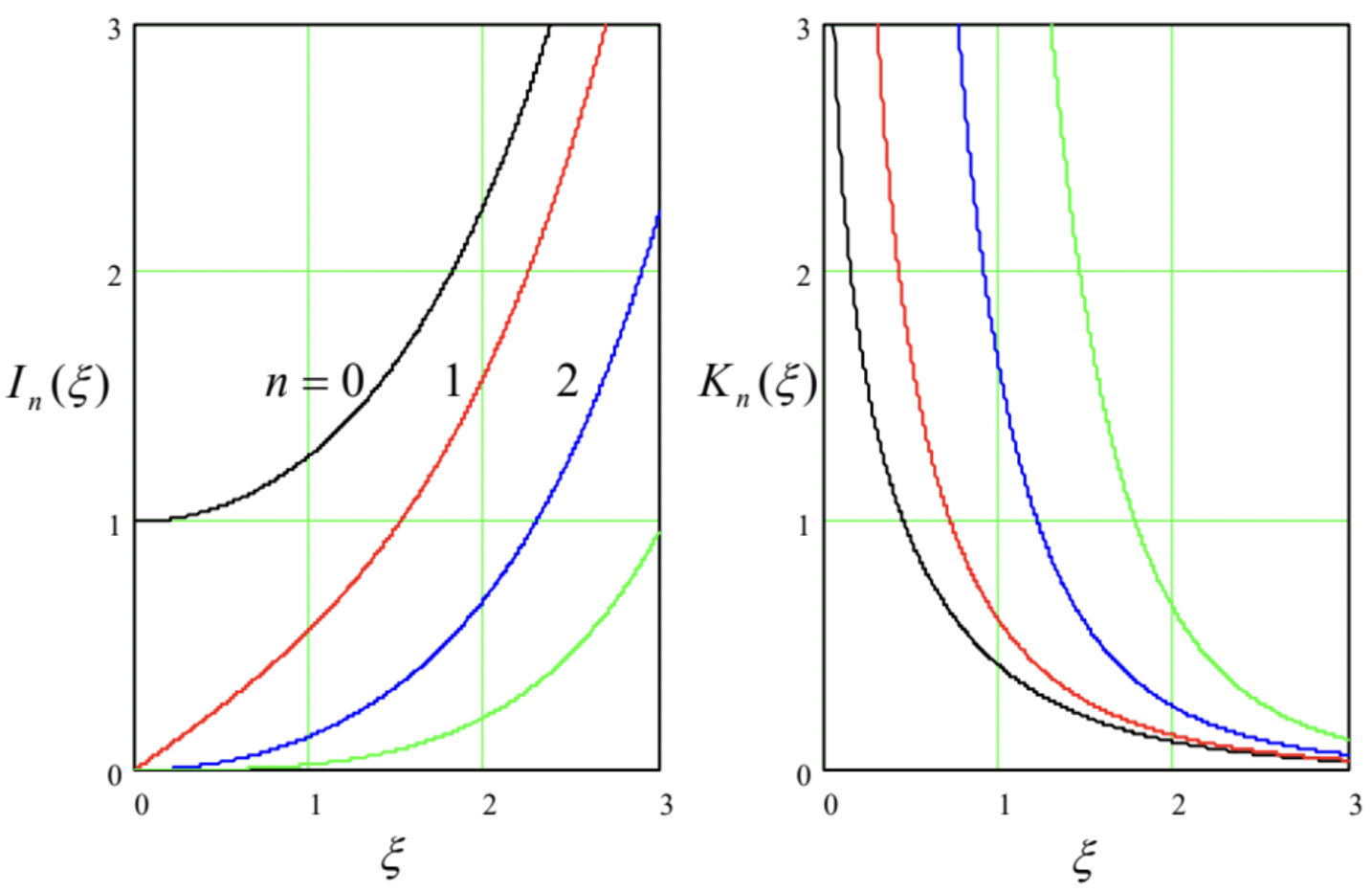
Este comportamiento es completamente natural en el contexto del problema mostrado en la Fig. 21, en el que el potencial electrostático puede representarse como una suma de términos proporcionales al\(\ I_{n}(\gamma \rho)\) interior de la tubería delgada, y de términos proporcionales al\(\ K_{n}(\gamma \rho)\) exterior de la misma.

Para completar nuestra breve encuesta de las funciones de Bessel, permítanme señalar que todas ellas discutidas hasta ahora pueden considerarse como casos particulares de las funciones de Bessel del argumento complejo, digamos\(\ J_{n}(\boldsymbol{z})\) y\(\ Y_{n}(\boldsymbol{z})\), o, alternativamente,\(\ H_{n}^{(1,2)}(\boldsymbol{z}) \equiv J_{n}(\boldsymbol{z}) \pm i Y_{n}(\boldsymbol{z})\). ⁴⁹ En eso, el “habitual” Bessel funciona\(\ J_{n}(\xi)\) y\(\ Y_{n}(\xi)\) puede considerarse como los conjuntos de valores de estas funciones generalizadas en el eje real\(\ (z=\xi)\), mientras que las funciones modificadas como su caso particular en\(\ \boldsymbol{z}=i \xi\), también con real\(\ \xi\):

\[\ I_{\nu}(\xi)=i^{-\nu} J_{\nu}(i \xi), \quad K_{\nu}(\xi)=\frac{\pi}{2} i^{\nu+1} H_{\nu}^{(1)}(i \xi).\tag{2.159}\]

Además, esta generalización de las funciones de Bessel a todo el plano complejo\(\ \boldsymbol{z}\) permite el uso de sus valores a lo largo de otras direcciones en ese plano, por ejemplo bajo ángulos\(\ \pi / 4 \pm \pi / 2\). Como resultado, se llega a las llamadas funciones Kelvin:

\ [\\ begin {alineado}
&\ nombreoperador {ber} _ {\ nu}\ xi+i\ nombreoperador {bei} _ {\ nu}\ xi\ equiv J_ {\ nu}\ left (\ xi e^ {-i\ pi/4}\ right),\\
&\ nombreoperador {ker} _ {\ nu}\ xi+i\ nombreoperador {kei} _ {\ nu}\ xi\ equiv i\ frac {\ pi} {2} H_ {\ nu} ^ {(1)}\ izquierda (\ xi e^ {-i 3\ pi/4}\ derecha),
\ end {alineado}\ tag {2.160}\]

que también son útiles para algunos problemas importantes en física e ingeniería. Desafortunadamente, no tengo tiempo/espacio para discutir estos problemas en este curso. ⁵⁰

---

Referencia

³⁹ Véase, por ejemplo, MA Ec. (10.3).

⁴⁰ Obsérvese que esta normalización es específica para cada valor del parámetro de separación de variables\(\ \gamma\). También, tenga en cuenta que la normalización carece de sentido para\(\ \gamma=0\), es decir, para el caso\(\ Z(z)=\text { const }\). Sin embargo, si necesitamos las soluciones parciales para este valor particular de\(\ \gamma\), siempre podemos usar las ecuaciones (108) - (109).

⁴¹ Para una discusión más completa de estas funciones, véase la literatura listada en MA Sec. 16, por ejemplo, el Capítulo 6 (escrito por F. Olver) en la famosa colección compilada y editada por Abramowitz y Stegun.

⁴² Estas dos fórmulas para el pico de la función de Bessel son estrictamente válidas para\(\ n \gg1\), pero pueden ser utilizadas para estimaciones razonables a partir ya de\(\ n=1\); por ejemplo,\(\ \max _{\xi}\left[J_{1}(\xi)\right]\) está cerca de 0.58 y se alcanza a\(\ \xi \approx 2.4\), a casi 30% de distancia de los valores dados por el asintótico fórmulas.

⁴³ Eq. (135) y la Fig. 18 muestran claramente la estrecha analogía entre las funciones de Bessel y las funciones trigonométricas habituales, seno y coseno. Para enfatizar esta similitud, y ayudar al lector a desarrollar más instinto de las funciones de Bessel, permítanme mencionar un hecho de la teoría de la elasticidad: mientras que las funciones sinusoidales describen, en particular, ondas estacionarias fundamentales en una cuerda de guitarra, las funciones\(\ J_{n}(\xi)\) describen, en particular, ondas estacionarias fundamentales en una membrana redonda elástica (digamos, un tambor redondo), con la\(\ J_{0}(\xi)\) descripción de su modo más bajo (fundamental), el único modo con una amplitud distinta de cero de las oscilaciones del centro de la membrana.

⁴⁴ Solo para la referencia del lector, las funciones de Bessel del mismo argumento pero diferentes órdenes también son ortogonales, pero de manera diferente:

\[\ \int_{0}^{\infty} J_{n}(\xi) J_{n^{\prime}}(\xi) \frac{d \xi}{\xi}=\frac{1}{n+n^{\prime}} \delta_{n n^{\prime}}.\]

⁴⁵ Estas relaciones proporcionan, en particular, una manera conveniente para el cálculo numérico de todos\(\ J_{n}(\xi)\) —después de\(\ J_{0}(\xi)\) que se haya calculado. (Este último se suele hacer usando la Ec. (132) para menor\(\ \xi\) y una extensión de la Ec. (135) para mayor\(\ \xi\).) Tenga en cuenta que la mayoría de los paquetes de software matemático, incluyendo todos los enumerados en MA Sec. 16 (iv), incluyen subrutinas listas para el cálculo de las funciones\(\ J_{n}(\xi)\) y otras funciones especiales utilizadas en esta serie de conferencias. En este sentido, la línea que separa estas “funciones especiales” de las “funciones elementales” es bastante fina.

⁴⁶ Véase, por ejemplo, MA Ec. (6.7a). Tenga en cuenta que\(\ \Gamma(s) \rightarrow \infty\) en\(\ s \rightarrow 0,-1,-2, \ldots\)

⁴⁷ A veces, se les llama las funciones de Neumann, y denotadas como\(\ N_{\nu}(\xi)\)

⁴⁸ Un par de funciones lineales independientes, utilizadas para la representación de la solución general de la ecuación de Bessel, también se pueden elegir de manera diferente, utilizando las llamadas funciones de Hankel

\[\ H_{n}^{(1,2)}(\xi) \equiv J_{n}(\xi) \pm i Y_{n}(\xi).\]

Para representar la solución general de la Ec. (130), esta alternativa es completamente similar, por ejemplo, a usar el par de funciones complejas\(\ \exp \{\pm i \alpha x\} \equiv \cos \alpha x \pm i \sin \alpha x\) en lugar del par de funciones reales\(\ \{\cos \alpha x, \sin \alpha x\}\) para la representación de la solución general de la Ec. (89) para\(\ X(x)\).

⁴⁹ Estas complejas funciones siguen obedeciendo las relaciones generales (143) y (146), con\(\ \xi\) sustituidas por\(\ \boldsymbol{z}\).

⁵⁰ En la parte QM de esta serie nos encontraremos con las llamadas funciones esféricas de Bessel\(\ j_{n}(\xi)\) y\(\ y_{n}(\xi)\), que pueden expresarse a través de las funciones de Bessel de órdenes semienteros. Sorprendentemente, estas funciones resultan ser más simples que\(\ J_{n}(\xi)\) y\(\ Y_{n}(\xi)\).