3.1: Dipolo eléctrico

Consideremos un sistema localizado de cargas, de una escala de tamaño lineal\(\ a\), y derivemos una expresión simple pero aproximada para el campo electrostático inducido por el sistema en un punto distante\(\ \mathbf{r}\). Para ello, seleccionemos un marco de referencia con el origen ya sea en algún lugar dentro del sistema, o a una distancia del orden\(\ a\) de éste (Fig. 1).

Fig. 3.1. Derivar la expresión aproximada para el campo electrostático de un sistema localizado de cargas en un punto distante\(\ \left(r>>r^{\prime} \sim a\right)\).

Entonces las posiciones de todos los cargos del sistema satisfacen la siguiente condición:

\[\ r^{\prime}<<r.\tag{3.1}\]

Usando esta condición, podemos expandir la expresión general (1.38) para el potencial electrostático\(\ \phi(\mathbf{r})\) del sistema a la serie Taylor en pequeño parámetro\(\ \mathbf{r}^{\prime}\). Para cualquier función de tipo\(\ f\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\), la expansión puede representarse como ¹

\[\ f\left(\mathbf{r}-\mathbf{r}^{\prime}\right)=f(\mathbf{r})-\sum_{j=1}^{3} r_{j}^{\prime} \frac{\partial f}{\partial r_{j}}(\mathbf{r})+\frac{1}{2 !} \sum_{j, j^{\prime}=1}^{3} r_{j}^{\prime} r_{j^{\prime}}^{\prime} \frac{\partial^{2} f}{\partial r_{j} \partial r_{j^{\prime}}}(\mathbf{r})-\ldots.\tag{3.2}\]

Aplicando esta fórmula a la función de Green de espacio libre\(\ 1 /\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\) en la Ec. (1.38), obtenemos la llamada expansión multipolar del potencial electrostático:

\[\ \phi(\mathbf{r})=\frac{1}{4 \pi \varepsilon_{0}}\left(\frac{1}{r} Q+\frac{1}{r^{3}} \sum_{j=1}^{3} r_{j} p_{j}+\frac{1}{2 r^{5}} \sum_{j, j^{\prime}=1}^{3} r_{j} r_{j^{\prime}}\mathscr{Q}_{j j^{\prime}}+\ldots\right),\tag{3.3}\]

cuyos parámetros\(\ \mathbf{r}\) -independientes se definen de la siguiente manera:

\[\ Q \equiv \int \rho\left(\mathbf{r}^{\prime}\right) d^{3} r^{\prime}, \quad p_{j} \equiv \int \rho\left(\mathbf{r}^{\prime}\right) r_{j}^{\prime} d^{3} r^{\prime}, \quad \mathscr{Q}_{j j^{\prime}} \equiv \int \rho\left(\mathbf{r}^{\prime}\right)\left(3 r_{j}^{\prime} r_{j^{\prime}}{ }^{\prime}-r^{\prime 2} \delta_{j j^{\prime}}\right) d^{3} r^{\prime}.\tag{3.4}\]

(De hecho, los dos términos principales de la expansión (2) pueden reescribirse en forma de vector\(\ f(\mathbf{r})-\mathbf{r}^{\prime} \cdot \nabla f(\mathbf{r})\), y el gradiente de tal función esféricamente simétrica\(\ f(r)=1 / r\) es justo\(\ \mathbf{n}_{r} d f / d r\), de modo que

\[\ \frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} \approx \frac{1}{r}-\mathbf{r}^{\prime} \cdot \mathbf{n}_{r} \frac{d}{d r}\left(\frac{1}{r}\right)=\frac{1}{r}+\mathbf{r}^{\prime} \cdot \frac{\mathbf{r}}{r^{3}},\tag{3.5}\]

dando inmediatamente los dos primeros términos de la Ec. (3). La prueba del tercer término cuadrupolo en la Ec. (3) es similar pero un poco más larga, y se deja para el ejercicio del lector.)

Evidentemente, el parámetro escalar\(\ Q\) en las ecuaciones (3) - (4) es solo la carga total del sistema. Las constantes\(\ p_{j}\) pueden considerarse como componentes cartesianos del siguiente vector:

Momento dipolo eléctrico

\[\ \mathbf{p} \equiv \int \rho\left(\mathbf{r}^{\prime}\right) \mathbf{r}^{\prime} d^{3} r^{\prime},\tag{3.6}\]

llamado momento dipolo eléctrico del sistema, y\(\ \mathcal{Q}_{j j^{\prime}}\) son los componentes cartesianos de un tensor — momento cuadrupolo eléctrico del sistema. Si\(\ Q \neq 0\), todos los términos superiores en el lado derecho de la Ecuación (3), a grandes distancias (1), son solo pequeñas correcciones a la primera, y en muchos casos pueden ser ignoradas. Sin embargo, la carga neta de muchos sistemas es exactamente cero, siendo los ejemplos más importantes los átomos y moléculas neutros. Para tales sistemas neuronales, el segundo término (dipolo-momento) en la Ec. (3) es, con mayor frecuencia, el principal. (Tales sistemas se llaman dipolos eléctricos). Por su importancia, reescribamos la expresión para este término en otras tres formas matemáticamente equivalentes:

Potencial del dipolo eléctrico

\[\ \phi_{\mathrm{d}} \equiv \frac{1}{4 \pi \varepsilon_{0}} \frac{\mathbf{r} \cdot \mathbf{p}}{r^{3}} \equiv \frac{1}{4 \pi \varepsilon_{0}} \frac{p \cos \theta}{r^{2}} \equiv \frac{1}{4 \pi \varepsilon_{0}} \frac{p z}{\left(x^{2}+y^{2}+z^{2}\right)^{3 / 2}},\tag{3.7}\]

que son más convenientes para algunas aplicaciones. Aquí\(\ \theta\) está el ángulo entre los vectores\(\ \mathbf{p}\) y\(\ \mathbf{r}\), y en la última representación (cartesiana), el eje z se dirige a lo largo del vector\(\ \mathbf{p}\). La figura 2a muestra las superficies equipotenciales del campo dipolar, o más bien sus secciones transversales por cualquier plano en el que\(\ \mathbf{p}\) resida el vector.

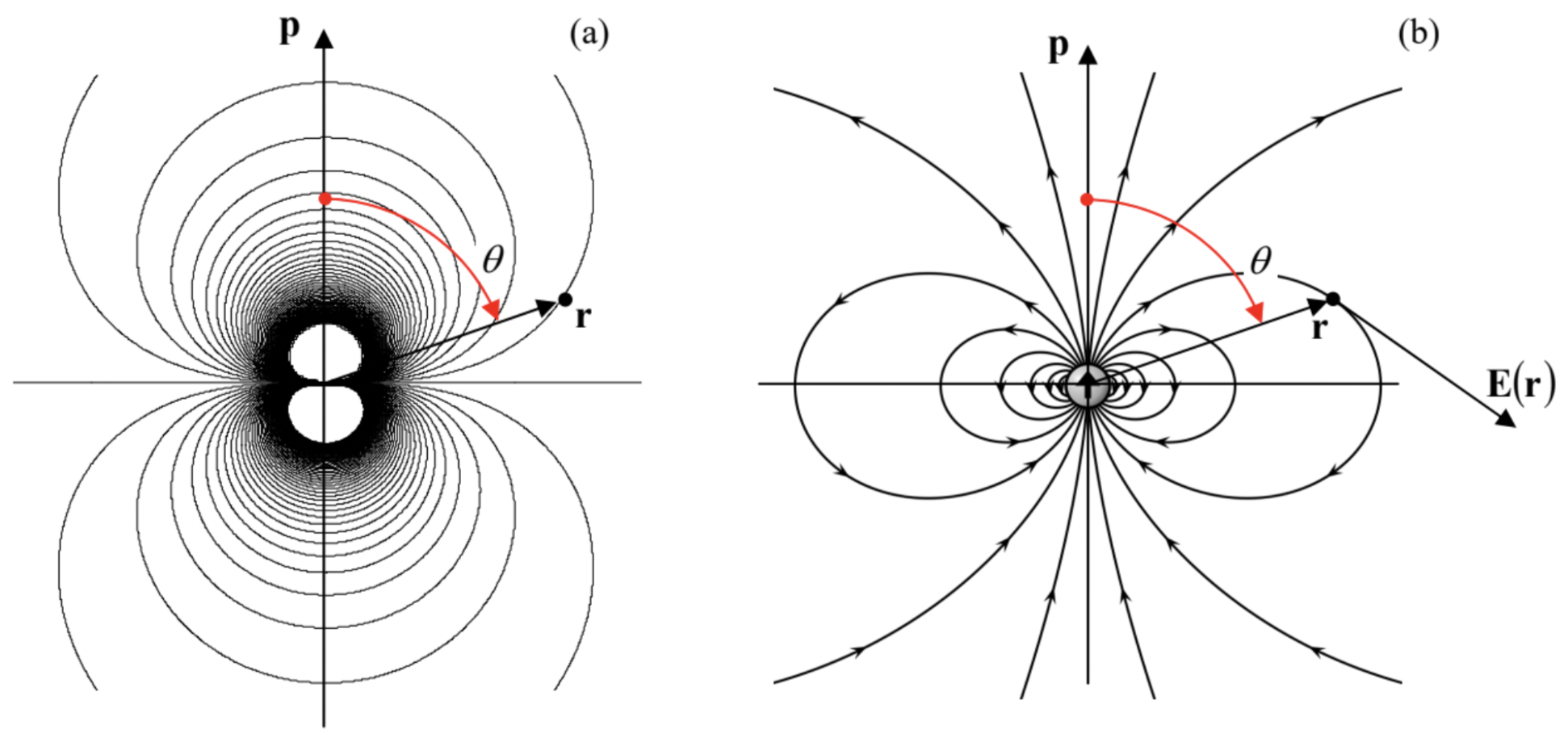Fig. 3.2. (a) Las superficies equipotenciales y (b) las líneas de campo eléctrico de un dipolo. (Panel (b) adaptado de http://en.Wikipedia.org/wiki/Dipole bajo la Licencia de Documentación Libre de GNU.)

El ejemplo más simple de un sistema cuyo campo, a grandes distancias, se acerca al campo dipolar (7), es dos cargas puntuales iguales pero opuestas (“polos”),\(\ +q\) y\(\ -q\), con los radio-vectores, respectivamente,\(\ \mathbf{r}_{+}\) y\(\ \mathbf{r}_{-}\):

\[\ \rho(\mathbf{r})=(+q) \delta\left(\mathbf{r}-\mathbf{r}_{+}\right)+(-q) \delta\left(\mathbf{r}-\mathbf{r}_{-}\right).\tag{3.8}\]

Para este sistema (a veces llamado el dipolo físico), la Ec. (4) rinde

\[\ \mathbf{p}=(+q) \mathbf{r}_{+}+(-q) \mathbf{r}_{-}=q\left(\mathbf{r}_{+}-\mathbf{r}_{-}\right)=q \mathbf{a},\tag{3.9}\]

donde\(\ \mathbf{a}\) esta el vector que conecta los puntos\(\ \mathbf{r}_{-}\) y\(\ \mathbf{r}_{+}\). Tenga en cuenta que en este caso (y de hecho para todos los sistemas con\(\ Q=0\)), el momento dipolar no depende de la elección del origen del marco de referencia.

Un ejemplo menos trivial de un dipolo es una esfera conductora de radio\(\ R\) en un campo eléctrico externo uniforme\(\ \mathbf{E}_{0}\). Como recordatorio, este problema se resolvió en la Sec. 2.8, y su resultado es expresado por la Ec. (2.176). El primer término entre paréntesis de esa relación describe solo el campo externo (2.173), de manera que el campo de la esfera misma (es decir, el de la carga superficial inducida por\(\ \mathbf{E}_{0}\)) viene dado por el segundo término:

\[\ \phi_{\mathrm{s}}=\frac{E_{0} R^{3}}{r^{2}} \cos \theta.\tag{3.10}\]

Comparando esta expresión con la segunda forma de la Ec. (7), vemos que la esfera tiene un momento dipolar inducido

\[\ \mathbf{p}=4 \pi \varepsilon_{0} \mathbf{E}_{0} R^{3}.\tag{3.11}\]

Este es un ejemplo interesante de un campo dipolar prácticamente puro: en todos los puntos fuera de la esfera\(\ (r>R)\), el campo no tiene ni un momento cuadrupolo ni ningún momento superior.

Otros ejemplos de campos dipolares son dados por dos sistemas más discutidos en el Capítulo 2 — ver Ecuaciones (2.215) y (2.219). Esos sistemas, sin embargo, sí tienen momentos multipolares de orden superior, de modo que para ellos, la ecuación (7) solo da la aproximación de larga distancia.

Ahora volviendo a las propiedades generales del campo dipolo (7), calculemos sus características. En primer lugar, podemos usar la ecuación (7) para calcular el campo eléctrico de un dipolo:

\[\ \mathbf{E}_{\mathrm{d}}=-\nabla \phi_{\mathrm{d}}=-\frac{1}{4 \pi \varepsilon_{0}} \nabla\left(\frac{\mathbf{r} \cdot \mathbf{p}}{r^{3}}\right)=-\frac{1}{4 \pi \varepsilon_{0}} \nabla\left(\frac{p \cos \theta}{r^{2}}\right).\tag{3.12}\]

La diferenciación es más fácil en las coordenadas esféricas, utilizando la expresión bien conocida para el gradiente de una función escalar en estas coordenadas ² y tomando el eje z paralelo al momento dipolar\(\ \mathbf{p}\). De la última forma de la Ec. (12), obtenemos inmediatamente

Campo de dipolo eléctrico

\[\ \mathbf{E}_{\mathrm{d}}=\frac{p}{4 \pi \varepsilon_{0} r^{3}}\left(2 \mathbf{n}_{r} \cos \theta+\mathbf{n}_{\theta} \sin \theta\right) \equiv \frac{1}{4 \pi \varepsilon_{0}} \frac{3 \mathbf{r}(\mathbf{r} \cdot \mathbf{p})-\mathbf{p} r^{2}}{r^{5}}.\tag{3.13}\]

La Fig. 2b anterior muestra las líneas de campo eléctrico dadas por las ecuaciones (13). Las características más importantes de este resultado son una caída más rápida de la magnitud del campo (\(\ E_{\mathrm{d}} \propto 1 / r^{3}\), en lugar\(\ E \propto 1 / r^{2}\) de una carga puntual), y el cambio de los signos de todos los componentes del campo como funciones del ángulo polar\(\ \theta\).

A continuación, utilicemos la ecuación (1.55) para calcular la energía potencial de interacción entre un dipolo y un campo eléctrico externo. Suponiendo que el campo externo no cambia mucho a distancias del orden de\(\ a\) (Fig. 1), podemos expandir su potencial\(\ \phi_{\mathrm{ext}}(\mathbf{r})\) a la serie Taylor, y mantener solo sus dos términos
principales:

\[\ U=\int \rho(\mathbf{r}) \phi_{\text {ext }}(\mathbf{r}) d^{3} r \approx \int \rho(\mathbf{r})\left[\phi_{\text {ext }}(0)+\mathbf{r} \cdot \nabla \phi_{\text {ext }}(0)\right] d^{3} r \equiv Q \phi_{\text {ext }}(0)-\mathbf{p} \cdot \mathbf{E}_{\text {ext }}.\tag{3.14}\]

El primer término es la energía potencial que tendría el sistema si fuera sólo una carga puntual. Si la carga neta\(\ Q\) es cero, ese término desaparece, y la contribución principal se debe al momento dipolar:

\[\ U=-\mathbf{p} \cdot \mathbf{E}_{\text {ext }}, \quad \text { for } \mathbf{p}=\text { const }.\tag{3.15a}\]

Energía del dipolo en campo externo

Tenga en cuenta que este resultado sólo es válido para un dipolo fijo, con\(\ \mathbf{p}\) independiente de\(\ \mathbf{E}_{\text {ext }}\). En el límite opuesto, cuando el dipolo es inducido por el campo, es decir\(\ \mathbf{p} \propto \mathbf{E}_{\text {ext }}\) (es posible que tenga una mirada más a la Ec. (11) para ver un ejemplo de tal proporcionalidad), necesitamos comenzar con la Ec. (1.60) en lugar de la Eq. (1.55), obteniendo

\[\ U=-\frac{1}{2} \mathbf{p} \cdot \mathbf{E}_{\text {ext }}, \quad \text { for } \mathbf{p} \propto \mathbf{E}_{\text {ext }}.\tag{3.15b}\]

En particular, combinando las ecuaciones (13) y la ecuación (15a), podemos obtener la siguiente fórmula importante para la interacción de dos dipolos independientes:

\[\ U_{\mathrm{int}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathbf{p}_{1} \cdot \mathbf{p}_{2} r^{2}-3\left(\mathbf{r} \cdot \mathbf{p}_{1}\right)\left(\mathbf{r} \cdot \mathbf{p}_{2}\right)}{r^{5}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{p_{1 x} p_{2 x}+p_{1 y} p_{2 y}-2 p_{1 z} p_{2 z}}{r^{3}},\tag{3.16}\]

donde\(\ \mathbf{r}\) está el vector que conecta los dipolos, y el eje z se dirige a lo largo de este vector. Es fácil demostrar (este ejercicio se deja para el lector) que si se fija la magnitud de cada momento dipolar (la aproximación válida, en particular, para la interacción débil de las llamadas moléculas polares), esta energía potencial alcanza su mínimo en, y por lo tanto favorece la orientación paralela de los dipolos a lo largo la línea que los conecta. Obsérvese también que en este caso,\(\ U_{\mathrm{int}}\) es proporcional a\(\ 1 / r^{3}\). Por otro lado, si cada momento\(\ \mathbf{p}\) tiene un valor aleatorio más un componente debido a su polarización por el campo eléctrico de su contraparte:\(\ \Delta \mathbf{p}_{1,2} \propto \mathbf{E}_{2,1} \propto 1 / r^{3}\), su energía de interacción promedio (que puede calcularse a partir de la Ec. (16) con el factor adicional 1⁄2) es siempre negativa y es proporcional a \(\ 1 / r^{6}\). Tal potencial negativo describe, en particular, la parte atractiva de largo alcance (la llamada fuerza de dispersión de Londres) de la interacción entre átomos y moléculas eléctricamente neutros. ³

Según las ecuaciones (15), para alcanzar el mínimo de\(\ U\), el campo eléctrico “intenta” alinear la dirección del dipolo a lo largo de la suya propia. La expresión cuantitativa de este efecto es la\(\ \boldsymbol{\tau}\) ejercida por el campo. La forma más sencilla de calcularlo es resumiendo todos los pares elementales\(\ d \boldsymbol{\tau}=\mathbf{r} \times d \mathbf{F}_{\mathrm{ext}}=\mathbf{r} \times \mathbf{E}_{\mathrm{ext}}(\mathbf{r}) \rho(\mathbf{r}) d^{3} r\) ejercidos sobre todas las cargas elementales del sistema:

\[\ \boldsymbol{\tau}=\int \mathbf{r} \times \mathbf{E}_{\text {ext }}(\mathbf{r}) \rho(\mathbf{r}) d^{3} r \approx \mathbf{p} \times \mathbf{E}_{\text {ext }}(0),\tag{3.17}\]

donde en el último paso se volvió a descuidar la dependencia espacial del campo externo. La dependencia espacial de\(\ \mathbf{E}_{\mathrm{ext}}\) no puede, sin embargo, ser ignorada en el cálculo de la fuerza total ejercida por el campo sobre el dipolo (con\(\ Q=0\)). En efecto, las ecuaciones (15) muestran que si el campo es constante, la energía del dipolo es la misma en todos los puntos espaciales, y de ahí que la fuerza neta sea cero. Sin embargo, si el campo tiene un gradiente distinto de cero, aparece una fuerza total; para un dipolo independiente del campo,

\[\ \mathbf{F}=-\nabla U=\nabla\left(\mathbf{p} \cdot \mathbf{E}_{\mathrm{ext}}\right),\tag{3.18}\]

donde la derivada tiene que ser tomada en la posición del dipolo (en nuestra notación, at\(\ \mathbf{r}=0\). Si el dipolo que se mueve en un campo conserva su magnitud y orientación, entonces la última fórmula es equivalente a ⁴

\[\ \mathbf{F}=(\mathbf{p} \cdot \nabla) \mathbf{E}_{\text {ext }}.\tag{3.19}\]

Alternativamente, la última expresión puede obtenerse de manera similar a la Ec. (14):

\[\ \mathbf{F}=\int \rho(\mathbf{r}) \mathbf{E}_{\mathrm{ext}}(\mathbf{r}) d^{3} r \approx \int \rho(\mathbf{r})\left[\mathbf{E}_{\mathrm{ext}}(0)+(\mathbf{r} \cdot \nabla) \mathbf{E}_{\mathrm{ext}}\right] d^{3} r=Q \mathbf{E}_{\mathrm{ext}}(0)+(\mathbf{p} \cdot \nabla) \mathbf{E}_{\mathrm{ext}}.\tag{3.20}\]

Por último, permítanme agregar una nota sobre el llamado modelo de grano grueso del dipolo. La aproximación del dipolo explorada anteriormente es asintóticamente correcta solo a grandes distancias,\(\ r \gg a\). Sin embargo, para algunas aplicaciones (incluyendo la próxima discusión de los efectos del campo molecular en la Sec. 3) es importante tener una expresión que sería aproximadamente válida en todas partes en el espacio, aunque tal vez sin detalles exactos en\(\ r \sim a\), y también dar el resultado correcto para el promedio espacial de el campo eléctrico,

\[\ \overline{\mathbf{E}} \equiv \frac{1}{V} \int_{V} \mathbf{E} d^{3} r,\tag{3.21}\]

donde\(\ V\) es un volumen de forma regular mucho mayor que\(\ a^{3}\), por ejemplo, una esfera de radio\(\ R \gg a\), con el dipolo en su centro. Para el campo\(\ \mathbf{E}_{\mathrm{d}}\) dado por la Ec. (13), tal promedio es cero. En efecto, consideremos los componentes cartesianos de ese vector en un marco de referencia con el eje z dirigido a lo largo del vector\(\ \mathbf{p}\). Debido a la simetría axial del campo, los promedios de los componentes\(\ E_{x}\) y\(\ E_{y}\) desaparecen. Usemos la ecuación (13) para deletrear el componente “vertical” del campo (paralelo al vector de momento dipolo):

\[\ E_{z} \equiv \mathbf{E}_{\mathrm{d}} \cdot \frac{\mathbf{p}}{p}=\frac{1}{4 \pi \varepsilon_{0} r^{3}}\left(2 \mathbf{n}_{r} \cdot \mathbf{p} \cos \theta-\mathbf{n}_{\theta} \cdot \mathbf{p} \sin \theta\right)=\frac{p}{4 \pi \varepsilon_{0} r^{3}}\left(2 \cos ^{2} \theta-\sin ^{2} \theta\right).\tag{3.22}\]

Integrando esta expresión sobre todo el ángulo sólido\(\ \Omega=4 \pi\), fijo\(\ r\), usando una conveniente sustitución de variables\(\ \cos \theta \equiv \xi\), obtenemos

\[\ \oint_{4 \pi} E_{z} d \Omega=2 \pi \int_{0}^{\pi} E_{z} \sin \theta d \theta=\frac{p}{2 \varepsilon_{0} r^{3}} \int_{0}^{\pi}\left(2 \cos ^{2} \theta-\sin ^{2} \theta\right) \sin \theta d \theta=\frac{p}{2 \varepsilon_{0} r^{3}} \int_{-1}^{+1}\left(3 \xi^{2}-1\right) d \xi=0.\tag{3.23}\]

Por otra parte, el campo eléctrico exacto de una distribución arbitraria de carga, con el momento dipolo total\(\ \mathbf{p}\), obedece a la siguiente igualdad:

\[\ \int_{V} \mathbf{E}(\mathbf{r}) d^{3} r=-\frac{\mathbf{p}}{3 \varepsilon_{0}} \equiv-\frac{1}{4 \pi \varepsilon_{0}} \frac{4 \pi}{3} \mathbf{p},\tag{3.24}\]

donde la integración se encuentra sobre cualquier esfera que contenga todas las cargas. Una prueba de esta fórmula para el caso general requiere una integración directa, pero algo tediosa. ⁵ El origen de la Ec. (24) se ilustra en la Fig. 3 en el ejemplo del dipolo creado por dos cargas iguales pero opuestas — ver Ecuaciones (8) - (9). El promedio cero (23) del campo dipolo (13) no toma en cuenta la contribución de la región entre las cargas (donde la ecuación (13) no es válida), la cual se dirige principalmente contra el vector dipolo (9).

Fig. 3.3. Un boceto que ilustra el origen de la Ec. (24).

Para ser utilizado como un modelo razonable de grano grueso, la Ec. (13) puede modificarse de la siguiente manera:

\[\ \mathbf{E}_{\mathrm{cg}}=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{3 \mathbf{r}(\mathbf{r} \cdot \mathbf{p})-\mathbf{p} r^{2}}{r^{5}}-\frac{4 \pi}{3} \mathbf{p} \delta(\mathbf{r})\right],\tag{3.25}\]

para que su promedio satisfaga la Ec. (24). Evidentemente, tal modificación no cambia el campo a grandes distancias\(\ r >> a\), es decir, en la región donde la expansión (3), y por lo tanto la Ec. (13), son válidas.

---

Referencia

¹ Véase, por ejemplo, MA Ec. (2.11b).

² Véase, por ejemplo, MA Ec. (10.8) con\(\ \partial / \partial \varphi=0\).

³ Esta fuerza se calcula, utilizando varios modelos, en las partes QM y SM de esta serie.

⁴ La equivalencia puede probarse, por ejemplo, mediante el uso de MA Ec. (11.6) con\(\ \mathbf{f}=\mathbf{p}=\text { const }\) y\(\ \mathbf{g}=\mathbf{E}_{\text {ext }}\), tomando en cuenta que de acuerdo con la Ec. general (1.28),\(\ \nabla \times \mathbf{E}_{\text {ext }}=0\).

⁵ Véase, por ejemplo, el final de la Sec. 4.1 en el libro de texto de J. Jackson, Classical Electrodynamics, 3 ^rd ed., Wiley, 1999.