4.3: Problemas de límites

Para un medio conductor óhmico, podemos combinar las ecuaciones (6) y (8) para obtener la siguiente ecuación diferencial

\[\ \nabla \cdot(\sigma \nabla \phi)=0.\tag{4.14}\]

Para un conductor uniforme\(\ (\sigma=\mathrm{const})\), la ecuación (14) se reduce a la ecuación de Laplace para el potencial electrostático (macroscópico)\(\ \phi\). Como ya sabemos de los Capítulos 2 y 3, su solución depende de las condiciones de contorno. Estas condiciones, a su vez, dependen del tipo de interfaz.

(i) Interfaz conductor-conductor. Aplicando la ecuación de continuidad (6) a un pastillero tipo Gauss en la interfaz de dos conductores diferentes (Fig. 5), obtenemos

\[\ \left(j_{n}\right)_{1}=\left(j_{n}\right)_{2},\tag{4.15}\]

de manera que si la ley Ohm (8) es válida dentro de cada medio, entonces

\[\ \sigma_{1} \frac{\partial \phi_{1}}{\partial n}=\sigma_{2} \frac{\partial \phi_{2}}{\partial n}.\tag{4.16}\]

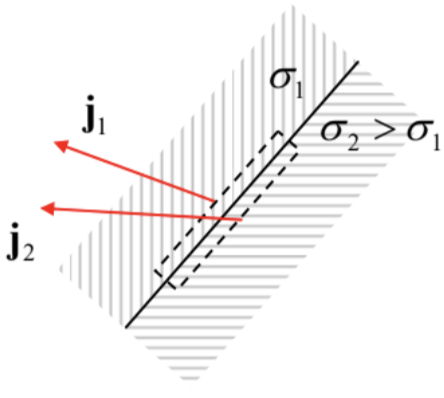Fig. 4.5. La “refracción” de la corriente CC en la interfaz entre dos conductores diferentes.

Además, dado que el campo eléctrico debe ser finito, su potencial\(\ \phi\) tiene que ser continuo a través de la interfaz, la condición que también puede escribirse como

\[\ \frac{\partial \phi_{1}}{\partial \tau}=\frac{\partial \phi_{2}}{\partial \tau}.\tag{4.17}\]

Ambas condiciones (y por lo tanto las soluciones de los problemas de límite que las utilizan) son similares a las de la interfaz entre dos dieléctricos — cf. Eq. (3.46) - (3.47). Tenga en cuenta que usando la ley Ohm, la Ec. (17) puede reescribirse como

\[\ \frac{1}{\sigma_{1}}\left(j_{\tau}\right)_{1}=\frac{1}{\sigma_{2}}\left(j_{\tau}\right)_{2}.\tag{4.18}\]

Comparándolo con la Ec. (15) vemos que, generalmente, la magnitud de la densidad de corriente cambia en la interfaz:\(\ j_{1} \neq j_{2}\). También es curioso que si\(\ \sigma_{1} \neq \sigma_{2}\), la pendiente actual de la línea cambia en la interfaz (Fig. 5), cualitativamente similar a la refracción de los rayos de luz en la óptica — ver Capítulo 7.

(ii) Interfaz conductor-electrodo. Un electrodo se define como un cuerpo hecho de un “conductor perfecto”, es decir, de un medio con\(\ \sigma \rightarrow \infty\). Entonces, a una densidad de corriente fija en la interfaz, el campo eléctrico en el electrodo tiende a cero, y por lo tanto puede describirse por la igualdad

\[\ \phi=\phi_{j}=\mathrm{const},\tag{4.19}\]

donde las constantes\(\ \phi_{j}\) pueden ser diferentes para diferentes electrodos (numerados con índice\(\ j\)). Tenga en cuenta que con tales condiciones de límite, el problema de límite de Laplace se vuelve exactamente el mismo que en la electrostática — véase la Ec. (2.35) — y por lo tanto podemos usar todos los métodos (y algunas soluciones: -) del Capítulo 2 para encontrar la distribución de corriente dc.

(iii) Interfaz conductor-aislador. Para la descripción de un buen aislante, podemos usar la igualdad\(\ \sigma=0\), de manera que la Ec. (16) produce la siguiente condición de límite,

\[\ \frac{\partial \phi}{\partial n}=0,\tag{4.20}\]

para la derivada potencial dentro del conductor. De la ley Ohm (8) en la forma\(\ \mathbf{j}=-\sigma \nabla \phi\), vemos que este es solo el requisito muy natural para que la corriente dc no fluya hacia un aislante. Ahora tenga en cuenta que esta condición hace que el problema de Laplace dentro del conductor esté completamente bien definido, e independiente de la distribución de potencial en el aislante adyacente. Por el contrario, debido a la continuidad del potencial electrostático en la frontera, su distribución dentro del aislador circundante tiene que seguir esa dentro del conductor.

Discutamos este tema conceptual en el siguiente ejemplo (aparentemente, trivial): corriente continua en un cable uniforme de longitud l y una sección transversal de área\(\ A\). El lector ciertamente sabe la respuesta:

\[\ I=\frac{V}{R}, \quad \text { where } R \equiv \frac{V}{I}=\frac{l}{\sigma A},\quad\quad\quad\quad\text{Uniform wire’s resistance}\tag{4.21}\]

donde la constante\(\ R\) se llama la resistencia. ¹⁴ Sin embargo, derivemos este resultado formalmente de nuestro marco teórico. Para la geometría simple que se muestra en la Fig. 6a, esto es fácil de hacer. Aquí el potencial evidentemente tiene una distribución lineal 1D

\[\ \phi=\text { const }-\frac{x}{l} V,\tag{4.22}\]

tanto en el conductor como en el espacio libre circundante, con ambas condiciones límite (16) y (17) satisfechas en las interfaces conductor-aislante, y la condición (20) satisfecha en las interfaces conductor-electrodo. Como resultado, el campo eléctrico es constante y tiene un solo componente\(\ E_{x}=V / l\), de modo que dentro del conductor

\[\ j_{x}=\sigma E_{x}, \quad I=j_{x} A,\tag{4.23}\]

dándonos la conocida Ec. (21).

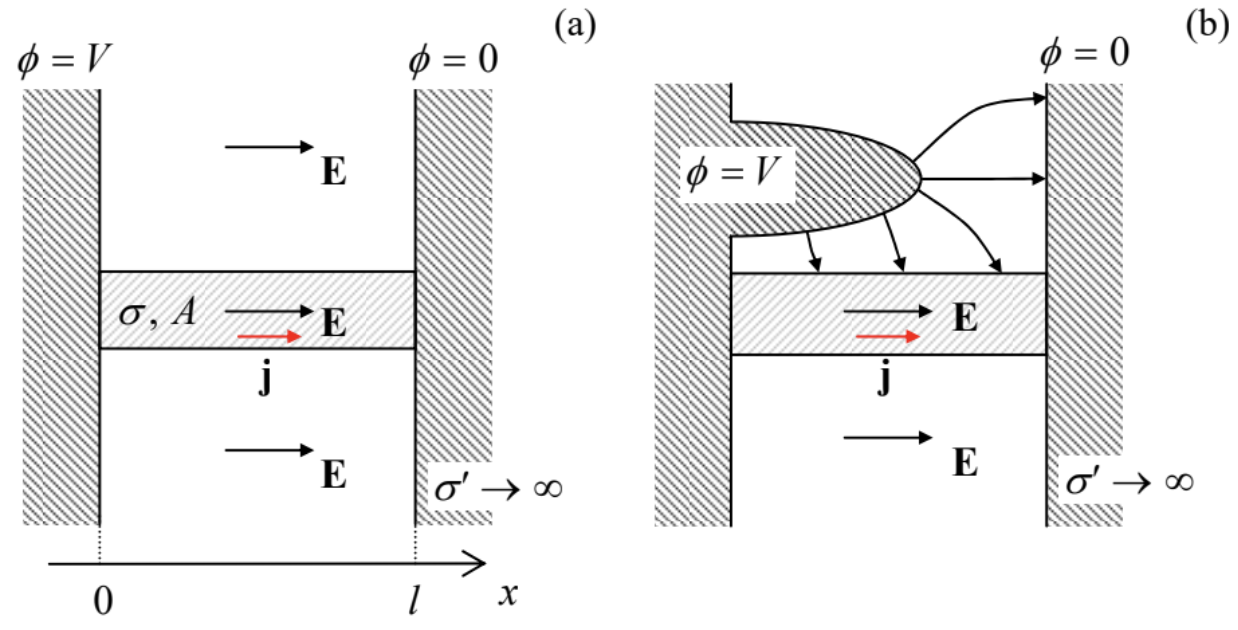Fig. 4.6. (a) Un problema elemental y (b) un problema (ligeramente) menos obvio de la distribución del campo en el flujo de corriente continua (esquemáticamente).

Sin embargo, ¿qué pasa con la geometría mostrada en la Fig. 6b? En este caso, la distribución del campo en el espacio libre alrededor del conductor es dramáticamente diferente, pero de acuerdo con el problema de límites definido por las ecuaciones (14) y (20), dentro del conductor, la solución es exactamente la misma que en el primer caso. Ahora, la ecuación de Laplace en el aislante circundante tiene que resolverse con los valores límite del potencial electrostático, “dictados” por la distribución de la corriente (y por lo tanto el potencial) en el conductor. Tenga en cuenta que como resultado, las líneas de campo eléctrico generalmente no son normales a la superficie del conductor, porque la superficie no es equipotencial.

Resolvamos un problema en que esta jerarquía de conducción puede seguirse analíticamente hasta el final. Considera una cavidad esférica vacía tallada en un conductor con un flujo de corriente inicialmente uniforme con una densidad constante\(\ \mathbf{j}_{0}=\mathbf{n}_{z} j_{0}\) (Fig. 7a). Siguiendo la jerarquía, tenemos que resolver el problema de límites en la parte conductora del sistema, es decir, fuera de la esfera\(\ (r \geq R)\), primero. Dado que el problema es evidentemente simétrico axialmente, ya conocemos la solución general de la ecuación de Laplace — véase la Ec. (2.172). Además, sabemos que para hacer coincidir la distribución uniforme del campo en\(\ r \rightarrow \infty\), todos los coeficientes menos\(\ a_{l}\) uno\(\ \left(a_{1}=-E_{0}=-j_{0} / \sigma\right)\) tienen que ser cero, y que las condiciones de contorno en\(\ r=R\) darán cero soluciones para todos los coeficientes menos\(\ b_{l}\) uno\(\ \left(b_{1}\right)\), de manera que

\[\ \phi=-\frac{j_{0}}{\sigma} r \cos \theta+\frac{b_{1}}{r^{2}} \cos \theta, \quad \text { for } r \geq R.\tag{4.24}\]

Para encontrar el coeficiente\(\ b_{1}\), tenemos que usar la condición de límite (20) en\(\ r=R\):

\[\ \left.\frac{\partial \phi}{\partial r}\right|_{r=R}=\left(-\frac{j_{0}}{\sigma}-\frac{2 b_{1}}{R^{3}}\right) \cos \theta=0.\tag{4.25}\]

Esto da\(\ b_{1}=-j_{0} R^{3} / 2 \sigma\), para que, finalmente,

\[\ \phi(r, \theta)=-\frac{j_{0}}{\sigma}\left(r+\frac{R^{3}}{2 r^{2}}\right) \cos \theta, \quad \text { for } r \geq R.\tag{4.26}\]

(Obsérvese que esta distribución de potencial corresponde al momento dipolar\(\ \mathbf{p}=-\mathbf{E}_{0} R^{3} / 2\). Es sencillo comprobar que si la cavidad esférica se cortara en un dieléctrico, la distribución de potencial fuera de ella sería similar, con\(\ \mathbf{p}=-\mathbf{E}_{0} R^{3}(\kappa-1) /(\kappa+2)\). En el límite\(\ \kappa \rightarrow \infty\), estos dos resultados coinciden, a pesar del tipo bastante diferente del problema: en el caso dieléctrico, no hay corriente en absoluto.)

Fig. 4.7. Una cavidad esférica tallada en un conductor uniforme: (a) la geometría del problema, y (b) las superficies equipotenciales dadas por las ecuaciones (26) y (28).

Ahora, como segundo paso en la jerarquía de conductividad, podemos encontrar la distribución del potencial electrostático\(\ \phi(r, \theta)\) en el aislante, en este caso particular dentro de la cavidad vacía\(\ (r \leq R)\). También debe satisfacer la ecuación de Laplace con los valores límite en\(\ r=R\), “dictados” por la distribución (26):

\[\ \phi(R, \theta)=-\frac{3}{2} \frac{j_{0}}{\sigma} R \cos \theta.\tag{4.27}\]

De nuevo podríamos resolver este problema por la separación de variables formales (manteniendo en la solución general (2.172) solo el término proporcional a\(\ a_{1}\), que no diverge en\(\ r \rightarrow 0\)), pero si observamos que la condición límite (27) depende de una sola coordenada cartesiana,\(\ z=R \cos \theta\), la solución puede se acaba de adivinar:

\[\ \phi(r, \theta)=-\frac{3}{2} \frac{j_{0}}{\sigma} z=-\frac{3}{2} \frac{j_{0}}{\sigma} r \cos \theta, \quad \text { at } r \leq R.\tag{4.28}\]

En efecto, evidentemente satisface la ecuación de Laplace y la condición límite (27), y corresponde a un campo eléctrico constante paralelo al vector\(\ \mathbf{J}_{0}\), e igual a\(\ 3 j_{0} / 2 \sigma\) — ver Fig. 7b. Nuevamente, la superficie de la cavidad no es equipotencial, y las líneas de campo eléctrico en no\(\ r \leq R\) son normales a ella en casi todos los puntos.

De manera más general, la jerarquía de conductividad dice que los campos eléctricos estáticos y las cargas fuera de los conductores (por ejemplo, cables eléctricos) no afectan a las corrientes que fluyen en los cables, y es físicamente muy claro por qué. Por ejemplo, si una carga en el espacio libre se mueve lentamente cerca de un cable, ésta (de acuerdo con el principio de superposición lineal) solo induce una carga superficial adicional (ver Sec. 2.1) que criba el campo de la carga externa, sin participar en el flujo de corriente dentro del conductor.

Además de esta cuestión conceptual, los dos ejemplos dados anteriormente pueden considerarse como aplicaciones de los dos primeros métodos discutidos en el Capítulo 2 —las coordenadas ortogonales (Fig. 6) y la separación de variables (Fig. 7) — a problemas de distribución de corriente continua. Como recordará el lector, ese capítulo también discutió el método de carga de imágenes, y también puede ser utilizado para la solución de algunos problemas de conductividad de CC. En efecto, consideremos la distribución del potencial esféricamente simétrico del potencial electrostático, similar a la dada por la ecuación básica (1.35):

\[\ \phi=\frac{c}{r}.\tag{4.29}\]

Como sabemos por el Capítulo 1, esta es una solución particular de la ecuación 3D Laplace en todos los puntos menos\(\ r=0\). En el espacio libre, esta distribución correspondería a una carga puntual\(\ q=4 \pi \varepsilon_{0} c\); pero ¿qué pasa con un conductor óhmico uniforme? Calcular el campo eléctrico y la densidad de corriente correspondientes,

\[\ \mathbf{E}=-\nabla \phi=\frac{c}{r^{3}} \mathbf{r}, \quad \mathbf{j}=\sigma \mathbf{E}=\sigma \frac{c}{r^{3}} \mathbf{r},\tag{4.30}\]

vemos que la corriente total que fluye desde el origen a través de una esfera de un radio arbitrario\(\ r\) no depende del radio:

\[\ I=A j=4 \pi r^{2} j=4 \pi \sigma c.\tag{4.31}\]

Tapando el coeficiente resultante\(\ c\) en la Ec. (29), obtenemos

\[\ \phi=\frac{I}{4 \pi \sigma r}.\tag{4.32}\]

De ahí que sea posible la distribución de tipo culombios del potencial eléctrico en un conductor (al menos a cierta distancia del punto singular\(\ r=0\)), y describe la corriente continua\(\ I\) que fluye fuera de un electrodo de pequeño tamaño, o hacia dicho electrodo si el coeficiente\(\ c\) es negativo. Dicha inyección de corriente puede implementarse fácilmente experimentalmente; piense, por ejemplo, en un cable aislado con un pequeño extremo desnudo, insertado en un suelo mal conductor, un método importante en la investigación geofísica. ¹⁵

Ahora deje que el punto de inyección de corriente\(\ \mathbf{r^{\prime}}\) esté cerca de una interfaz plana entre el conductor y un aislante (Fig. 8). En este caso, además de la ecuación de Laplace, debemos satisfacer la condición límite,

\[\ j_{n}=\sigma E_{n}=-\sigma \frac{\partial \phi}{\partial n}=0,\tag{4.33}\]

en la interfaz. Es claro que esto se puede hacer reemplazando el aislador por un conductor similar imaginario con un punto de inyección de corriente adicional, en el punto de imagen especular\(\ \mathbf{r^{\prime\prime}}\). Obsérvese, sin embargo, que a diferencia de las imágenes de carga, el signo de la corriente imaginaria tiene que ser similar, no opuesto, al inicial, de manera que el potencial electrostático total dentro del semiespacio conductor sea

\[\ \phi(\mathbf{r})=\frac{I}{4 \pi \sigma}\left(\frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}+\frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime \prime}\right|}\right).\tag{4.34}\]

(El signo de la corriente de imagen sería opuesto en la interfaz entre un conductor con una conductividad moderada y un conductor perfecto (“electrodo”), cuyo potencial debería ser prácticamente constante).

Fig. 4.8. Aplicando el método de imágenes para el análisis de inyección actual.

Este resultado se puede utilizar fácilmente, por ejemplo, para calcular la densidad de corriente en una superficie plana de un conductor uniforme, en función de la distancia\(\ \rho\) desde el punto 0, el punto de la superficie más cercano al sitio de inyección de corriente — ver Fig. 8. En dicha superficie, la Ec. (34) rinde

\[\ \phi=\frac{I}{2 \pi \sigma} \frac{1}{\left(\rho^{2}+d^{2}\right)^{1 / 2}},\tag{4.35}\]

para que la densidad de corriente sea:

\[\ j_{\rho}=\sigma E_{\rho}=-\sigma \frac{\partial \phi}{\partial \rho}=\frac{I}{2 \pi} \frac{\rho}{\left(\rho^{2}+d^{2}\right)^{3 / 2}}.\tag{4.36}\]

Las desviaciones de las ecuaciones (35) y (36) pueden utilizarse para encontrar y caracterizar las inhomogeneidades de conductancia, digamos, las debidas a depósitos minerales en la corteza terrestre. ¹⁶

---

Referencia

¹⁴ La primera de las ecuaciones (21) es esencialmente la forma integral (históricamente, inicial) de la ley Ohm, y es válida no solo para un cable uniforme, sino también para conductores óhmicos de cualquier geometría en eso\(\ I\) y\(\ V\) puede estar claramente definido.

¹⁵ Tal inyección es aún más simple en situaciones 2D: piense en un alambre soldado, en un punto pequeño, a una delgada lámina conductora. (Obsérvese solo que aquí la ley de distribución de densidad de corriente es diferente,\(\ j \propto 1 / r\) más que\(\ 1 / r^{2}\).)

¹⁶ La inyección de corriente también puede ser producida, debido a reacciones electroquímicas, por una masa de mineral en sí misma, de manera que uno solo necesita medir (e interpretar correctamente :-) la distribución de potencial resultante —el llamado método de autopotencial— ver, por ejemplo, Sec. 6.1 en W. Telford et al., Applied Geophysics , ^2ª ed., Cambridge U. Press, 1990.