5.1: Interacción Magnética de Corrientes

Las corrientes de CC en los conductores suelen dejarlos electroneutrales\(\ \rho(\mathbf{r})=0\),, con muy buena precisión, ya que incluso un minuto de desequilibrio de densidad de carga positiva y negativa da como resultado fuerzas Coulomb extremadamente fuertes que restablecen su equilibrio por un cambio adicional de portadores de carga libre. Es por ello que iniciemos la discusión del magnetismo a partir del caso más simple de dos conductores electroneutrales espacialmente separados, portadores de corriente continua (Fig. 1).

Fig. 5.1. Interacción magnética de dos corrientes.

De acuerdo con la ley de Coulomb, no hay fuerza electrostática entre ellos. Sin embargo, varios experimentos realizados en 1820 ¹ demostraron que existe una interacción magnética diferente entre las corrientes. En la notación actual, los resultados de todos estos experimentos pueden resumirse con una sola fórmula, en unidades SI expresadas como:

\[\ \text{Magnetic force}\quad\quad\quad\quad\mathbf{F}=-\frac{\mu_{0}}{4 \pi} \int_{V} d^{3} r \int_{V^{\prime}} d^{3} r^{\prime}\left[\mathbf{j}(\mathbf{r}) \cdot \mathbf{j}^{\prime}\left(\mathbf{r}^{\prime}\right)\right] \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}\tag{5.1}\]

Aquí el coeficiente\(\ \mu_{0} / 4 \pi\) (donde\(\ \mu_{0}\) se llama la constante magnética o la permeabilidad del espacio libre) es igual a casi exactamente unidades\(\ 10^{-7}\) SI, con el producto\(\ \varepsilon_{0} \mu_{0}\) igual a exactamente\(\ 1 / c^{2}\). ²

Obsérvese una estrecha similitud de esta expresión con la ley Coulomb (1.1), escrita para distribuciones continuas de carga, con la cuenta del principio de superposición lineal (1.4):

\[\ \text{Electric force}\quad\quad\quad\quad\mathbf{F}=\frac{1}{4 \pi \varepsilon_{0}} \int_{V} d^{3} r \int_{V^{\prime}} d^{3} r^{\prime} \rho(\mathbf{r}) \rho^{\prime}\left(\mathbf{r}^{\prime}\right) \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}.\tag{5.2}\]

Además del coeficiente diferente y un signo diferente, la “única” diferencia de la Ec. (1) de la ecuación (2) es el producto escalar de las densidades de corriente, evidentemente necesaria por su carácter vectorial. Veremos que esta diferencia trae ciertas complicaciones en la aplicación de los enfoques discutidos en los capítulos anteriores, a la magnetostática.

Antes de ir a su discusión, echemos una mirada más a los coeficientes en las ecuaciones (1) y (2). Para compararlos, consideremos dos objetos con distribuciones de carga no compensadas\(\ \rho(\mathbf{r})\) y\(\ \rho^{\prime}(\mathbf{r})\), cada uno moviéndose paralelo entre sí en su conjunto, con ciertas velocidades\(\ \mathbf{v}\) y\(\ \mathbf{v^{\prime}}\), según se mide en el mismo marco de referencia inercial (“laboratorio”). En este caso,\(\ \mathbf{j}(\mathbf{r})=\rho(\mathbf{r}) \mathbf{v}\), así que\(\ \mathbf{j}(\mathbf{r}) \cdot \mathbf{j}^{\prime}(\mathbf{r})=\rho(\mathbf{r}) \rho^{\prime}(\mathbf{r}) \nu \nu^{\prime}\), y las integrales en las ecuaciones (1) y (2) se vuelven funcionalmente similares, difiriendo solo por el factor

\[\ \frac{F_{\text {magnetic }}}{F_{\text {electric }}}=-\frac{\mu_{0} \nu\nu^{\prime}}{4 \pi} / \frac{1}{4 \pi \varepsilon_{0}} \equiv-\frac{\nu \nu^{\prime}}{c^{2}}.\tag{5.3}\]

(La última expresión es válida en cualquier sistema consistente de unidades.) Inmediatamente vemos que el magnetismo es un fenómeno esencialmente relativista, muy débil en comparación con la interacción electrostática a las velocidades de escala humana\(\ \nu<<c\), y puede dominar sólo si esta última interacción se desvanece —como lo hace en los sistemas electroneutrales. ³ El descubrimiento y los estudios iniciales ⁴ de un fenómeno relativista tan sutil como el magnetismo se vieron muy facilitados por la abundancia relativa de ferroimanes naturales, materiales con polarización magnética espontánea, cuyo fuerte campo magnético se debe a efectos relativistas (como el espín) dentro de los átomos constituyentes — ver Sec. 5 a continuación.

También, la Ec. (3) apunta a una paradoja interesante. Considera dos haces de electrones que se mueven paralelos entre sí, con la misma velocidad v con respecto a un marco de referencia de laboratorio. Entonces, según la Ec. (3), la fuerza neta de su interacción total (eléctrica más magnética) es proporcional a\(\ \left(1-\nu^{2} / c^{2}\right)\), tendiendo a cero en el límite\(\ \nu \rightarrow c\). Sin embargo, en el marco de referencia que se mueve junto con los electrones, no se mueven en absoluto, es decir\(\ \nu=0\). De ahí que, desde el punto de vista de tal observador en movimiento, los haces de electrones deben interactuar solo electrostáticamente, con una fuerza repulsiva independiente de la velocidad\(\ \nu\). Históricamente, esta había sido una de varias paradojas que llevaron al desarrollo de una relatividad especial; su resolución será discutida en el Capítulo 9 dedicado a esta teoría.

Volviendo a la Ec. (1), en algunos casos simples la doble integración en ella puede llevarse a cabo analíticamente. En primer lugar, simplifiquemos esta expresión para el caso de dos conductores delgados y largos (“cables”) separados por una distancia mucho mayor que su grosor. En este caso, podemos integrar primero los productos\(\ \mathbf{j} d^{3} r\) y\(\ \mathbf{j}^{\prime} d^{3} r^{\prime}\) sobre las secciones transversales de los cables, descuidando el cambio correspondiente del factor\(\ \left(\mathbf{r}-\mathbf{r}^{\prime}\right)\). Dado que las integrales de la densidad de corriente sobre las secciones transversales de los cables son solo las corrientes\(\ I\) y\(\ I^{\prime}\) fluyen en los cables, y no pueden cambiar a lo largo de sus longitudes (digamos\(\ l^{\prime}\),\(\ l\) y, respectivamente), pueden extraerse de las integrales restantes, reduciendo la Ec. (1) a

\[\ \mathbf{F}=-\frac{\mu_{0} I I^{\prime}}{4 \pi} \oint_{l} \oint_{l^{\prime}}\left[d \mathbf{r} \cdot d \mathbf{r}^{\prime}\right] \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}.\tag{5.4}\]

Como ejemplo más sencillo, considera dos alambres rectos y paralelos (Fig. 2) separados por distancia\(\ d\), ambos con longitud\(\ l >> d\).

Fig. 5.2. La fuerza magnética entre dos corrientes paralelas rectas.

En este caso, debido a la simetría, el vector de la fuerza de interacción magnética tiene que:

(i) se encuentran en el mismo plano que las corrientes, y

(ii) ser normal a los cables — ver Fig. 2.

Por lo tanto, podemos limitar nuestros cálculos a un solo componente de la fuerza, normal a los cables. Utilizando el hecho de que con la elección de coordenadas mostrada en la Fig. 2, el producto escalar

\(\ d \mathbf{r} \cdot d \mathbf{r}^{\prime}\)es justo\(\ d x d x\), obtenemos

\[\ F=-\frac{\mu_{0} I I^{\prime}}{4 \pi} \int_{-\infty}^{+\infty} d x \int_{-\infty}^{+\infty} d x^{\prime} \frac{\sin \theta}{d^{2}+\left(x-x^{\prime}\right)^{2}}=-\frac{\mu_{0} I I^{\prime}}{4 \pi} \int_{-\infty}^{+\infty} d x \int_{-\infty}^{+\infty} d x^{\prime} \frac{d}{\left[d^{2}+\left(x-x^{\prime}\right)^{2}\right]^{3 / 2}}.\tag{5.5}\]

Ahora introduciendo, en lugar de\(\ x^{\prime}\), una nueva variable adimensional\(\ \xi \equiv\left(x-x^{\prime}\right) / d\), podemos reducir la integral interna a una tabla, que ya hemos encontrado en este curso:

\[\ F=-\frac{\mu_{0} I I^{\prime}}{4 \pi d} \int_{-\infty}^{+\infty} d x \int_{-\infty}^{+\infty} \frac{d \xi}{\left(1+\xi^{2}\right)^{3 / 2}}=-\frac{\mu_{0} I I^{\prime}}{2 \pi d} \int_{-\infty}^{+\infty} d x.\tag{5.6}\]

La integral sobre diverge\(\ x\) formalmente, pero da una fuerza de interacción finita por unidad de longitud de los cables:

\[\ \frac{F}{l}=-\frac{\mu_{0} I I^{\prime}}{2 \pi d}.\tag{5.7}\]

Tenga en cuenta que la fuerza cae bastante lentamente (solo como\(\ 1 / d\)) a medida que aumenta la distancia\(\ d\) entre los cables, y es atractiva (en lugar de repulsiva como en la ley de Coulomb) si las corrientes son del mismo signo.

Este es un resultado importante, ⁵ pero nuevamente, los problemas tan simplemente solucionables son pocos y distantes entre sí, y es intuitivamente claro que nos beneficiaríamos fuertemente del mismo enfoque que en la electrostática, es decir, de romper la Ec. (1) en un producto de dos factores a través de la introducción de un campo adecuado. Dicha descomposición se puede hacer de la siguiente manera:

\[\ \text{Lorentz force: current}\quad\quad\quad\quad\mathbf{F}=\int_{V} \mathbf{j}(\mathbf{r}) \times \mathbf{B}(\mathbf{r}) d^{3} r\tag{5.8}\]

donde el vector\(\ \mathbf{B}\) se llama campo magnético. ⁶ En el caso cuando sea inducido por la corriente\(\ \mathbf{j^{\prime}}\):

\ [\\ mathbf {B} (\ mathbf {r})\ equiv\ frac {\ mu_ {0}} {4\ pi}\ int_ {V^ {\ prime}}\ mathbf {j} ^ {\ prime}\ left (\ mathbf {r} ^ {\ prime}\ derecha)\ veces\ frac {\ mathbf {r} -\ mathbf {r} ^ {\ prime}} {\ izquierda|\ mathbf {r} -\ mathbf {r} ^ {\ prime}\ derecha|^ {3}} d^ {3} r^ {\ prime}. \ quad\ quad\ quad\ quad\ text {
ley Biot-Savart}\ tag {5.9}\]

A la última relación se le llama ley Biot-Savart, ⁷ mientras que la fuerza\(\ \mathbf{F}\) expresada por la ecuación (8) a veces se llama fuerza Lorentz. ^Sin embargo, con mayor frecuencia este último término se reserva para toda la fuerza,

\[\ \mathbf{F}=q(\mathbf{E}+\mathbf{v} \times \mathbf{B}),\quad\quad\quad\quad\text{Lorentz force: particle}\tag{5.10}\]

ejercido por campos eléctricos y magnéticos sobre una carga puntual\(\ q\), moviéndose con velocidad\(\ \mathbf{v}\). ⁹

Ahora tenemos que demostrar que la nueva formulación, dada por las Ecuaciones (8) - (9), es equivalente a la Eq. (1). A primera vista, esto parece poco probable. De hecho, en primer lugar, las ecuaciones (8) y (9) involucran productos vectoriales, mientras que la ecuación (1) se basa en un producto escalar. Más profundamente, en contraste con la ecuación (1), las ecuaciones (8) y (9) no satisfacen la ^tercera ley de Newton aplicada a los componentes elementales de corriente\(\ \mathbf{j} d^{3} r\) y\(\ \text { j' } d^{3} r^{\prime}\), si estos vectores no son paralelos entre sí. En efecto, considere la situación que se muestra en la Fig. 3.

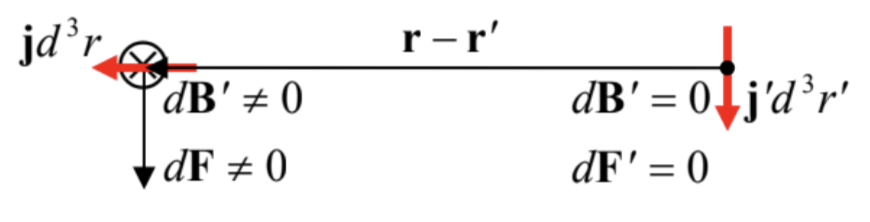Fig. 5.3. La aparente violación de la ^tercera ley Newton en el magnetismo.

Aquí el vector\(\ \mathbf { j' }\) es perpendicular al vector\(\ \left(\mathbf{r}-\mathbf{r}^{\prime}\right)\), y por lo tanto, de acuerdo con la Ec. (9), produce una contribución distinta de cero\(\ d \mathbf{B}^{\prime}\) al campo magnético, dirigida (en la Fig. 3) normalmente al plano del dibujo, es decir, es perpendicular al vector\(\ \mathbf{j}\). De ahí que, de acuerdo con la Ec. (8), este campo proporciona una contribución distinta de cero a\(\ \mathbf{F}\). Por otro lado, si calculamos la fuerza recíproca\(\ \mathbf{F}^{\prime}\) intercambiando los índices primos en las ecuaciones (8) y (9), esta última ecuación inmediatamente lo muestra\(\ d \mathbf{B}\left(\mathbf{r}^{\prime}\right) \propto \mathbf{j} \times\left(\mathbf{r}^{\prime}-\mathbf{r}\right)=0\), debido a que los dos vectores de operando son paralelos —véase nuevamente la Fig. 3. De ahí que el componente actual\(\ \mathbf{j}^{\prime} d^{3} \mathbf{r}^{\prime}\) sí ejerce una fuerza sobre su contraparte, mientras que\(\ \mathbf{j} d^{3} \mathbf{r}\) no.

A pesar de este aparente problema, sigamos adelante y conectemos la Ec. (9) a la Ec. (8):

\[\ \mathbf{F}=\frac{\mu_{0}}{4 \pi} \int_{V} d^{3} r \int_{V^{\prime}} d^{3} r^{\prime} \mathbf{j}(\mathbf{r}) \times\left(\mathbf{j}^{\prime}\left(\mathbf{r}^{\prime}\right) \times \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}\right).\tag{5.11}\]

Este producto de doble vector puede transformarse en dos productos escalares, usando la identidad algebraica del vector llamada regla bac menos cab,\(\ \mathbf{a} \times(\mathbf{b} \times \mathbf{c})=\mathbf{b}(\mathbf{a} \cdot \mathbf{c})-\mathbf{c}(\mathbf{a} \cdot \mathbf{b})\). ¹⁰ Aplicando esta relación, con\(\ \mathbf{a}=\mathbf{j}\)\(\ \mathbf{b}=\mathbf{j}^{\prime}\), y\(\ \mathbf{c}=\mathbf{R} \equiv \mathbf{r}-\mathbf{r^{\prime}}\), a la Ec. (11), obtenemos

\[\ \mathbf{F}=\frac{\mu_{0}}{4 \pi} \int_{V^{\prime}} d^{3} r^{\prime} \mathbf{j}^{\prime}\left(\mathbf{r}^{\prime}\right)\left(\int_{V} d^{3} r \frac{\mathbf{j}(\mathbf{r}) \cdot \mathbf{R}}{R^{3}}\right)-\frac{\mu_{0}}{4 \pi} \int_{V} d^{3} r \int_{V^{\prime}} d^{3} r^{\prime} \mathbf{j}(\mathbf{r}) \cdot \mathbf{j}^{\prime}\left(\mathbf{r}^{\prime}\right) \frac{\mathbf{R}}{R^{3}}.\tag{5.12}\]

El segundo término en el lado derecho de esta igualdad coincide con el lado derecho de la Ecuación (1), mientras que el primer término equivale a cero porque su integral interna se desvanece. En efecto, podemos romper los volúmenes\(\ V\) y\(\ V^{\prime}\) en tubos de corriente estrechos —los volúmenes elementales estirados cuyas paredes no están atravesadas por líneas
actuales (de manera que en sus paredes,\(\ j_{n}=0\). Como resultado, la corriente elemental en cada tubo,\(\ dI=jdA=j d^{2} r\), es la misma a lo largo de su longitud, y, al igual que en un cable delgado,\(\ \mathbf{j} d^{2} r\) puede ser reemplazada por\(\ d I d \mathbf{r}\), con el vector\(\ d \mathbf{r}\) dirigido a lo largo\(\ \mathbf{j}\). Debido a esto, la contribución de cada tubo a la integral interna en el primer término de la ecuación (12) puede representarse como

\[\ d I \oint_{l} d \mathbf{r} \cdot \frac{\mathbf{R}}{R^{3}}=-d I \oint_{l} d \mathbf{r} \cdot \nabla \frac{1}{R}=-d I \oint_{l} d r \frac{\partial}{\partial r} \frac{1}{R},\tag{5.13}\]

donde el operador\(\ \nabla\) actúa en el\(\ \mathbf{r}\) espacio, y la integral se toma a lo largo de la longitud del tubo\(\ l\). Debido a la continuidad de corriente expresada por la ecuación (4.6), cada bucle debe seguir un contorno cerrado, y una integral de un diferencial completo de alguna función escalar (en nuestro caso, 1/R) a lo largo de dicho contorno es igual a cero.

Así que hemos recuperado la Ec. (1). Volviendo por un minuto a la paradoja ilustrada con la Fig. 3, podemos concluir que la aparente violación de la ^tercera ley Newton fue el artefacto de nuestra interpretación de las ecuaciones (8) y (9) como las sumas de componentes elementales independientes. En realidad, debido a la continuidad de corriente continua, estos componentes no son independientes. Para todas las corrientes, las ecuaciones (8) a (9) sí obedecen a la\(\ 3^{\mathrm{rd}}\) ley —como se desprende de su ya probada equivalencia a la Ec. (1).

Así, hemos podido romper la interacción magnética en dos efectos: la inducción del campo magnético\(\ \mathbf{B}\) por una corriente (en nuestra notación,\(\ \mathbf{ j’ }\)), y el efecto de este campo sobre la otra corriente (\(\ \mathbf{j}\)). Ahora viene un hecho experimental adicional: otros componentes elementales\(\ \mathbf{j} d^{3} r^{\prime}\) de la corriente\(\ \mathbf{j}(\mathbf{r})\) también contribuyen al campo magnético (9) que actúa sobre el componente\(\ \mathbf{j} d^{3} r\). ¹¹ Este hecho nos permite dejar caer el signo primo después\(\ \mathbf{j}\) en la ecuación (9), y reescribir las ecuaciones (8) y (9) como

\[\ \mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V^{\prime}} \mathbf{j}\left(\mathbf{r}^{\prime}\right) \times \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} r^{\prime},\tag{5.14}\]

\[\ \mathbf{F}=\int_{V} \mathbf{j}(\mathbf{r}) \times \mathbf{B}(\mathbf{r}) d^{3} r.\tag{5.15}\]

Nuevamente, el punto de observación de campo r y el punto de origen de campo\(\ \mathbf{r}^{\prime}\) tienen que distinguirse claramente. Inmediatamente vemos que estas expresiones son cercanas, pero aún diferentes de las relaciones correspondientes de la electrostática, es decir, la Ec. (1.9) y la versión de carga distribuida de la Ec. (1.6):

\[\ \mathbf{E}(\mathbf{r})=\frac{1}{4 \pi \varepsilon_{0}} \oint_{V^{\prime}} \rho\left(\mathbf{r}^{\prime}\right) \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} r^{\prime},\tag{5.16}\]

\[\ \mathbf{F}=\oint_{V} \rho(\mathbf{r}) \mathbf{E}(\mathbf{r}) d^{3} r.\tag{5.17}\]

(Obsérvese que la diferencia de signos ha desaparecido, a costa de la sustitución de multiplicaciones escalar por vector en electrostática con productos cruzados de vectores en magnetostáticos.)

Para el caso frecuente de un campo de un cable delgado de longitud\(\ l'\), la ecuación (14) puede reescribirse como

\[\ \mathbf{B}(\mathbf{r})=\frac{\mu_{0} I}{4 \pi} \oint_{l^{\prime}} d \mathbf{r}^{\prime} \times \frac{\mathbf{r}-\mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}.\tag{5.18}\]

Veamos cómo funciona esta fórmula para el caso más simple de un cable recto (Fig. 4a). Las contribuciones del campo magnético\(\ d \mathbf{B}\) debido a todos los pequeños fragmentos\(\ d \mathbf{r}^{\prime}\) de la longitud del cable se dirigen a lo largo de la misma línea (perpendicular tanto al cable como a la normal\(\ d\) caída desde el punto de observación a la línea del cable), y su magnitud es

\[\ d B=\frac{\mu_{0} I}{4 \pi} \frac{d x^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{2}} \sin \theta=\frac{\mu_{0} I}{4 \pi} \frac{d x^{\prime}}{\left(d^{2}+x^{2}\right)} \frac{d}{\left(d^{2}+x^{2}\right)^{1 / 2}}.\tag{5.19}\]

Resumiendo todas esas contribuciones elementales, obtenemos

\[\ B=\frac{\mu_{0} I \rho}{4 \pi} \int_{-\infty}^{\infty} \frac{d x}{\left(x^{2}+d^{2}\right)^{3 / 2}}=\frac{\mu_{0} I}{2 \pi d}.\tag{5.20}\]

Fig. 5.4. Cálculo de campos magnéticos: (a) de una corriente recta, y (b) de un bucle de corriente.

Este es un resultado sencillo pero importante. (Tenga en cuenta que solo es válido para cables rectos muy largos\(\ (l >> d)\)). Es especialmente crucial notar el carácter “vórtice” del campo: sus líneas van alrededor del alambre, formando anillos con los centros en la línea actual. Esto está en marcado contraste con las líneas de campo electrostático, que solo pueden comenzar y terminar con cargas eléctricas y nunca formar bucles cerrados (de lo contrario la fuerza de Coulomb no\(\ q \mathbf{E}\) sería conservadora). En el caso magnético, la estructura de vórtice del campo puede conciliarse con el carácter potencial de las fuerzas magnéticas, lo cual es evidente a partir de la ecuación (1), debido a los productos vectoriales en las ecuaciones (14) - (15).

Ahora podemos usar fácilmente la ecuación (15), o más bien su versión de cable delgado

\[\ \mathbf{F}=I \oint_{l} d \mathbf{r} \times \mathbf{B}(\mathbf{r}),\tag{5.21}\]

para aplicar la Eq. (20) al problema de dos hilos (Fig. 2). Ya que para el segundo alambre vectores\(\ \mathrm{d} \mathbf{r}\) y\(\ \mathbf{B}\) son perpendiculares entre sí, llegamos inmediatamente a nuestro resultado anterior (7), el cual se obtuvo directamente de la Ec. (1).

El siguiente ejemplo importante de la aplicación de la ley Biot-Savart (14) es el campo magnético en el eje de un bucle de corriente circular (Fig. 4b). Debido a la simetría del problema, el campo neto\(\ \mathbf{B}\) tiene que ser dirigido a lo largo del eje, pero cada uno de sus componentes elementales\(\ \mathrm{d} \mathbf{B}\) está inclinado por el ángulo\(\ \theta=\tan ^{-1}(z / R)\) a este eje, de manera que su componente axial es

\[\ d B_{z}=d B \cos \theta=\frac{\mu_{0} I}{4 \pi} \frac{d r^{\prime}}{R^{2}+z^{2}} \frac{R}{\left(R^{2}+z^{2}\right)^{1 / 2}}.\tag{5.22}\]

Dado que el denominador de esta expresión sigue siendo el mismo para todos los componentes de cable\(\ d r^{\prime}\), la integración\(\ \mathbf{r}^{\prime}\) es fácil\(\ (\int d r^{\prime}=2 \pi R)\), dando finalmente

\[\ B=\frac{\mu_{0} I}{2} \frac{R^{2}}{\left(R^{2}+z^{2}\right)^{3 / 2}}.\tag{5.23}\]

Tenga en cuenta que el campo magnético en el centro del bucle (es decir, for\(\ z=0\)),

\[\ B=\frac{\mu_{0} I}{2 R},\tag{5.24}\]

es\(\ \pi\) veces mayor que eso debido a una corriente similar en un cable recto, a distancia\(\ d=R\) de él. Esta diferencia es fácilmente comprensible, ya que todos los componentes elementales del bucle están a la misma\(\ R\) distancia del punto de observación, mientras que en el caso de un alambre recto, todos sus puntos menos uno están separados del punto de observación por distancias mayores que\(\ d\).

Otro dato notable es que a grandes distancias\(\ \left(z^{2} >> R^{2}\right)\), el campo (23) es proporcional a\(\ z^{-3}\):

\[\ B \approx \frac{\mu_{0} I}{2} \frac{R^{2}}{|z|^{3}} \equiv \frac{\mu_{0}}{4 \pi} \frac{2 m}{|z|^{3}}, \quad \text { with } m \equiv I A,\tag{5.25}\]

donde\(\ A=\pi R^{2}\) está el área de bucle. Comparando esta expresión con la Ec. (3.13), para el caso particular\(\ \theta=0\), vemos que dicho campo es similar al de un dipolo eléctrico (al menos a lo largo de su dirección), con la sustitución de la magnitud\(\ p\) del momento dipolo eléctrico por la m así definida —además del factor frontal. En efecto, tal bucle de corriente plano es el ejemplo más simple de un sistema cuyo campo, a distancias mucho mayores que\(\ R\), es el de un dipolo magnético, con un momento dipolo\(\ \mathbf{m}\) —las nociones que se discutirán con más detalle en la Sec. 4 a continuación.

---

Referencia

¹ En particular, de Hans Christian Ørsted, quien descubrió el efecto de las corrientes eléctricas en las agujas magnéticas, y André-Marie Ampère, quien ha ampliado esta obra al encontrar la interacción magnética entre dos corrientes.

² Para más detalles, consulte el apéndice CA: Constantes Físicas Seleccionadas. En las unidades gaussianas, el coeficiente\(\ \mu_{0} / 4 \pi\) se sustituye por\(\ 1 / c^{2}\).

³ Un caso importante en el que la electroneutralidad puede no sostenerse es el movimiento de electrones en vacío. (Sin embargo, en este caso la velocidad de los electrones suele ser comparable con la velocidad de la luz, por lo que las fuerzas magnéticas pueden ser comparables en fuerza con las fuerzas electrostáticas, y por lo tanto importantes). En algunos dispositivos semiconductores, las violaciones locales de la electroneutralidad también juegan un papel importante —véase, por ejemplo, SM Capítulo 6.

⁴ El primer libro detallado sobre este tema, De Magnete de William Gilbert (alias Gilberd), fue publicado ya en 1600.

⁵ En particular, hasta muy recientemente (2018), se utilizó la Ec. (7) para la definición legal de la unidad SI de corriente, un amperio (A), vía la unidad SI de fuerza (el newton, N), con el coeficiente\(\ \mu_{0}\) considerado exactamente fijo.

⁶ La unidad SI del campo magnético se llama tesla (T) —después de Nikola Tesla, un pionero de la ingeniería eléctrica. En las unidades gaussianas, la constante ya discutida\(\ 1 / c^{2}\) en la ecuación (1) se divide equitativamente entre las ecuaciones (8) y (9), de manera que en ambas, la constante antes de la integral es\(\ 1 / c\). La unidad gaussiana resultante del campo\(\ \mathbf{B}\) se llama gauss (G); tomando en cuenta la diferencia de unidades de carga eléctrica y longitud, y por lo tanto de la densidad de corriente, 1 G es igual exactamente\(\ 10^{-4} \mathrm{~T}\). Obsérvese también que en algunos libros de texto, especialmente los antiguos,\(\ \mathbf{B}\) se denomina ya sea la inducción magnética o la densidad de flujo magnético, mientras que el término “campo magnético” se reserva para el campo\(\ \mathbf{H}\) que se introducirá en la Sec. 5 a continuación.

⁷ Nombrado en honor a Jean-Baptiste Biot y Félix Savart quienes hicieron varias contribuciones clave a la teoría de las interacciones magnéticas —en el mismo notorio 1820.

⁸ El nombre de Hendrik Antoon Lorentz, famoso principalmente por sus numerosas contribuciones al desarrollo de la relatividad especial — véase el Capítulo 9 a continuación. Para ser justos, la parte magnética de la fuerza Lorentz fue descrita implícitamente en un artículo mucho anterior (1865) de J. C. Maxwell, y luego deletreada por Oliver Heaviside (otro genio de la ingeniería eléctrica — ¡y las matemáticas!) en 1889, es decir, también antes de la obra de 1895 de H. Lorentz.

⁹ De la parte magnética de la Ec. (10), la ecuación (8) puede derivarse por la suma elemental de todas las fuerzas que actúan sobre las\(\ n >> 1\) partículas en un volumen unitario, con\(\ \mathbf{j}=q n \mathbf{v}\) — ver la nota al pie de página en la Ec. (4.13a). Por otro lado, la derivación recíproca de la Ec. (10) de la Ec. (8) con\(\ \mathbf{j}=q \mathbf{v} \delta\left(\mathbf{r}-\mathbf{r}_{0}\right)\), donde\(\ \mathbf{r}_{0}\) está la posición de la partícula actual (de manera que\(\ d \mathbf{r}_{0} / d t=\mathbf{v}\)), requiere cuidado y se realizará en el Capítulo 9.

¹⁰ Véase, por ejemplo, MA Ec. (7.5).

¹¹ Al igual que en la electrostática, hay que actuar con la debida precaución transformando estas expresiones para el límite de partículas clásicas discretas, y las funciones de onda extendidas en la mecánica cuántica, para evitar la interacción magnética (inexistente) de una partícula cargada consigo misma.