5.2: Potencial vectorial y la Ley Ampère

El lector pudo ver que los cálculos del campo magnético utilizando la ecuación (14) o (18) siguen siendo algo engorrosos incluso para los sistemas muy simples que hemos examinado. Como vimos en el Capítulo 1, cálculos similares en electrostática, al menos para varios sistemas importantes de alta simetría, podrían simplificarse sustancialmente usando la ley Gauss (1.16). También existe una relación similar en la magnetostática, pero tiene una forma diferente, debido al carácter vórtice del campo magnético.

Para derivarlo, notemos que en una analogía con el caso escalar, el producto vector bajo la integral (14) puede transformarse como

\[\ \frac{j\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}}=\nabla \times \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|},\tag{5.26}\]

donde el operador\(\ \nabla\) actúa en el\(\ \mathbf{r}\) -espacio. (Esta igualdad puede ser fácilmente verificada por sus componentes cartesianos, notando que la densidad de corriente es una función de\(\ \mathbf{r}^{\prime}\) y, por lo tanto, sus componentes son independientes de\(\ \mathbf{r}\).) Conectando la Eq. (26) en la Ecuación (14), y moviendo al operador\(\ \nabla\) fuera de la integral\(\ \mathbf{r}^{\prime}\), vemos que el campo magnético puede representarse como el rizo de otro campo vectorial, el llamado potencial vectorial, definido como: ¹²

Potencial vectorial

\[\ \mathbf{B}(\mathbf{r}) \equiv \nabla \times \mathbf{A}(\mathbf{r}),\tag{5.27}\]

y en nuestro caso actual igual a

\[\ \mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V^{\prime}} \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} r^{\prime}.\tag{5.28}\]

Tenga en cuenta una hermosa analogía entre las ecuaciones (27) - (28) y, respectivamente, las ecuaciones (1.33) y (1.38). Esta analogía implica que el potencial vectorial\(\ \mathbf { A }\) juega, para el campo magnético, esencialmente el mismo papel que\(\ \phi\) juega el potencial escalar para el campo eléctrico (de ahí el nombre de “potencial”), con el debido respeto al carácter vórtice de\(\ \mathbf{B}\). Esta noción se discutirá con más detalle a continuación.

Ahora veamos qué ecuaciones podemos obtener para las derivadas espaciales del campo magnético. Primero, el álgebra vectorial dice que la divergencia de cualquier rizo es cero. ¹³ En aplicación a la Ec. (27), esto significa que

\[\ \nabla \cdot \mathbf{B}=0.\quad\quad\quad\quad\text{No magnetic monopoles}\tag{5.29}\]

Comparando esta ecuación con la Ec. (1.27), vemos que la Ec. (29) puede interpretarse como la ausencia de un análogo magnético de una carga eléctrica, sobre la cual podrían originarse o terminar líneas de campo magnético. Numerosas búsquedas de tales cargas magnéticas hipotéticas, llamadas monopolos magnéticos, utilizando configuraciones experimentales muy sensibles y sofisticadas, no han dado ninguna evidencia confiable de su existencia en la Naturaleza.

Procediendo a la alternativa, vector derivado del campo magnético, es decir, su rizo, y usando la Ec. (28), obtenemos

\[\ \nabla \times \mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \nabla \times\left(\nabla \times \int_{V^{\prime}} \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} r^{\prime}\right).\tag{5.30}\]

Esta expresión puede simplificarse usando la siguiente identidad de vector general: ¹⁴

\[\ \nabla \times(\nabla \times \mathbf{c})=\nabla(\nabla \cdot \mathbf{c})-\nabla^{2} \mathbf{c},\tag{5.31}\]

aplicado al vector\(\ \mathbf{c}(\mathbf{r}) \equiv \mathbf{j}\left(\mathbf{r}^{\prime}\right) /\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\):

\[\ \nabla \times \mathbf{B}=\frac{\mu_{0}}{4 \pi} \nabla \int_{V^{\prime}} \mathbf{j}\left(\mathbf{r}^{\prime}\right) \cdot \nabla \frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} r^{\prime}-\frac{\mu_{0}}{4 \pi} \int_{V^{\prime}} \mathbf{j}\left(\mathbf{r}^{\prime}\right) \nabla^{2} \frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} r^{\prime}.\tag{5.32}\]

Como ya se discutió durante nuestro estudio de electrostática en la Sec. 3.1,

\[\ \nabla^{2} \frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}=-4 \pi \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right),\tag{5.33}\]

para que el último término de la Eq. (32) sea justo\(\ \mu_{0} \mathbf{j}(\mathbf{r})\). Por otro lado, dentro de la primera integral podemos\(\ \nabla\) sustituir por\(\ \left(-\nabla^{\prime}\right)\), donde primo significa diferenciación en el espacio del radio-vector\(\ \mathbf{r^{\prime}}\). Integrando ese término por partes, obtenemos

\[\ \nabla \times \mathbf{B}=-\frac{\mu_{0}}{4 \pi} \nabla \oint_{S^{\prime}} j_{n}\left(\mathbf{r}^{\prime}\right) \frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{2} r^{\prime}+\nabla \int_{V^{\prime}} \frac{\nabla^{\prime} \cdot \mathbf{j}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} r^{\prime}+\mu_{0} \mathbf{j}(\mathbf{r}).\tag{5.34}\]

Aplicando esta igualdad al volumen\(\ V^{\prime}\) limitado por una superficie\(\ S^{\prime}\) ya sea suficientemente distante de la concentración de campo, o sin corriente que la cruce, podemos descuidar el primer término en el lado derecho de la Ec. (34), mientras que el segundo término siempre es igual a cero en estática, debido a la carga dc continuidad — véase la Ec. (4.6). Como resultado, llegamos a una ecuación diferencial muy simple ¹⁵

\[\ \nabla \times \mathbf{B}=\mu_{0} \mathbf{j}.\tag{5.35}\]

Esta es (la forma dc de) la ecuación no homogénea de Maxwell, que en la magnetostática juega un papel similar al de la ecuación (1.27) en electrostática. Permítanme mostrar, por primera vez en este curso, este sistema fundamental de ecuaciones (en esta etapa, solo para la estática), y darle al lector un minuto para mirar, en silencio, a su hermosa simetría —que ha inspirado gran parte del desarrollo físico posterior:

\ [\\ text {Maxwell ecuaciones: estática}\ quad\ quad\ quad\ quad\ quad\ begin {array} {ll}
\ nabla\ veces\ mathbf {E} =0, &\ nabla\ veces\ mathbf {B} =\ mu_ {0}\ mathbf {j},
\\ nabla\ cdot\ mathbf {E} =\ frac {\ rho} {varepsilon_ {0}}, &\ nabla\ cdot\ mathbf {B} =0.
\ end {array}\ tag {5.36}\]

Su única asimetría, dos ceros en los lados de la derecha (para la divergencia del campo magnético y el rizo del campo eléctrico), se debe a la ausencia en la Naturaleza de los monopolos magnéticos y sus corrientes. Discutiré estas ecuaciones con más detalle en la Sec. 6.7, después de que las dos primeras ecuaciones (para los rizos de los campos) se hayan generalizado a sus versiones completas, dependientes del tiempo.

Volviendo ahora a nuestra tarea actual, más mundana pero importante de calcular el campo magnético inducido por simples configuraciones de corriente, podemos beneficiarnos de una forma integral de la Ec. (35). Para ello, integremos esta ecuación sobre una superficie arbitraria\(\ S\) limitada por un contorno cerrado\(\ C\), y apliquemos al resultado el teorema de Stokes. ¹⁶ La expresión resultante,

\[\ \text{Ampère law}\quad\quad\quad\quad \oint_{C} \mathbf{B} \cdot d \mathbf{r}=\mu_{0} \oint_{S} j_{n} d^{2} r \equiv \mu_{0} I,\tag{5.37}\]

donde\(\ I\) se encuentra la corriente eléctrica neta que cruza la superficie\(\ S\), se llama la ley Ampère.

Como primer ejemplo de su aplicación, volvamos a la corriente en un cable recto (Fig. 4a). Con la ley Ampère en nuestro arsenal, podemos perseguir fácilmente una meta aún más ambiciosa que la alcanzada en la sección anterior: calcular el campo magnético tanto fuera como dentro de un alambre de un radio arbitrario\(\ R\), con una distribución de corriente arbitraria (aunque axialmente simétrica)\(\ j(\rho)\) — ver Fig. 5.

Fig. 5.5. La aplicación más simple de la ley Ampère: el campo magnético de una corriente recta.

Seleccionando el contorno Ampère-law\(\ C\) en forma de anillo de algún radio\(\ \rho\) en el plano normal al eje del alambre\(\ z\), tenemos\(\ \mathbf{B} \cdot d \mathbf{r}=B \rho d \varphi\), donde\(\ \varphi\) está el ángulo azimutal, de manera que la Ec. (37) rinde:

\[\ 2 \pi \rho B(\rho)=\mu_{0} \times \begin{cases}2 \pi \int_{0}^{\rho} j\left(\rho^{\prime}\right) \rho^{\prime} d \rho^{\prime}, & \text { for } \rho \leq R, \\ 2 \pi \int_{0}^{R} j\left(\rho^{\prime}\right) \rho^{\prime} d \rho^{\prime} \equiv I, & \text { for } \rho \geq R.\end{cases}\tag{5.38}\]

De esta manera no sólo hemos recuperado nuestro resultado anterior (20), con el reemplazo de notación\(\ d \rightarrow \rho\), de una manera mucho más sencilla, sino que también pudimos encontrar la distribución del campo magnético dentro del alambre. En el caso más común cuando la corriente se distribuye uniformemente a lo largo de su sección transversal\(\ j(\rho)=\text { const }\),, la primera de Eqs. (38) cede inmediatamente\(\ B \propto \rho\) para\(\ \rho \leq R\).

Otro sistema importante es un solenoide recto, largo (Fig. 6a), con devanado denso:\(\ n^{2} A >> 1\), donde\(\ n\) está el número de vueltas de cable por unidad de longitud, y\(\ A\) es el área de la sección transversal del solenoide.

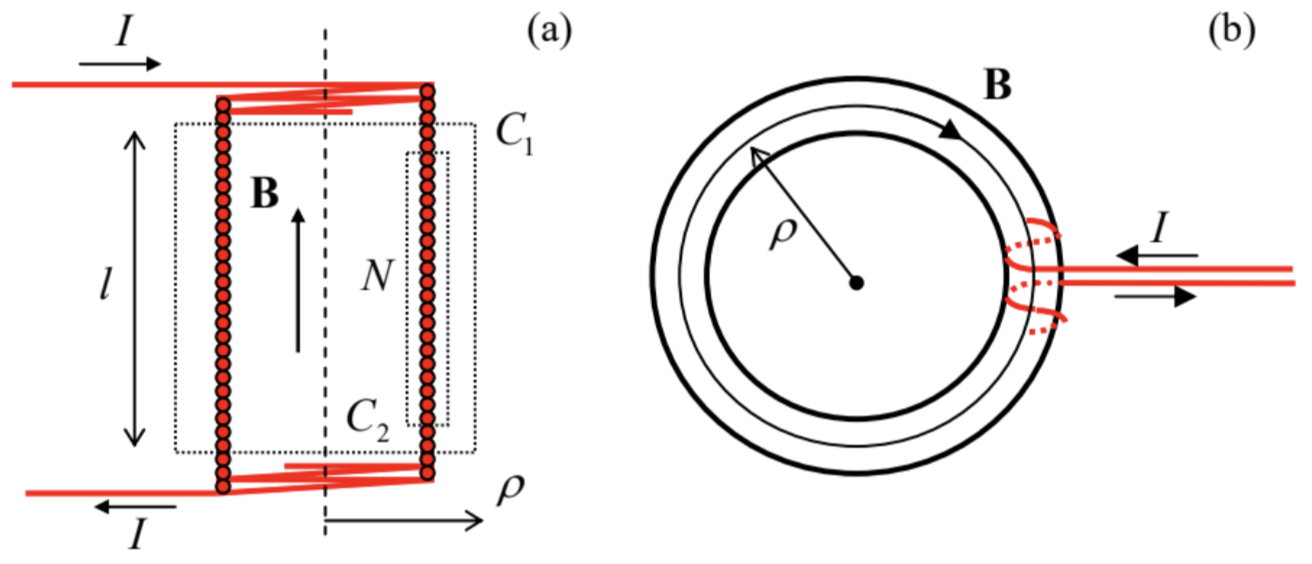Fig. 5.6. Cálculo de campos magnéticos de (a) solenoides rectos y (b) toroidales.

A partir de la simetría de este problema, la componente longitudinal (en la Fig. 6a, vertical)\(\ B_{z}\) del campo magnético sólo puede depender de la distancia\(\ \rho\) del punto de observación desde el eje del solenoide. Primero tomando un plano Ampère contorno\(\ C_{1}\), con ambos lados largos fuera del solenoide, obtenemos\(\ B_{z}\left(\rho_{2}\right)-B_{z}\left(\rho_{1}\right)=0\), porque la corriente total que perfora el contorno es igual a cero. Esto sólo es posible si\(\ B_{z}=0\) en cualquier\(\ \rho\) exterior del solenoide, siempre que sea infinitamente largo. ¹⁷ Con este resultado a la mano, de la ley Ampère aplicada al contorno\(\ C_{2}\), obtenemos la siguiente relación para el único (z-) componente del campo interno:

\[\ B l=\mu_{0} N I,\tag{5.39}\]

donde\(\ N\) es el número de vueltas de alambre que pasan por el contorno de longitud\(\ l\). Esto significa que independientemente de la posición exacta del lado interno del contorno, el resultado es el mismo:

\[\ B=\mu_{0} \frac{N}{l} I \equiv \mu_{0} n I.\tag{5.40}\]

Así, el campo dentro de un solenoide infinitamente largo (con una forma arbitraria de su sección transversal) es uniforme; en este sentido, un solenoide largo es un análogo magnético de un condensador de plano ancho, explicando por qué este sistema es tan ampliamente utilizado en el experimento físico.

Como debe quedar claro a partir de su derivación, los resultados obtenidos, especialmente que el campo exterior del solenoide es igual a cero, están condicionados a que la longitud del solenoide sea muy grande en comparación con su tamaño lateral. (A partir de la Ec. (25), podemos predecir que para un solenoide de una longitud finita\(\ l\), el campo externo de rango cercano es un factor de\(\ \sim A / l^{2}\) menor que el interno). Se puede obtener una supresión mucho mejor de este campo de “franja” usando el solenoide toroidal (Fig. 6b). La aplicación de la ley Ampère a esta geometría muestra que en el límite del devanado denso\(\ (N >> 1)\), no hay campo de flecos en absoluto (para cualquier relación entre dos radios del toro), mientras que dentro del solenoide, a\(\ \rho\) distancia del eje del sistema,

\[\ B=\frac{\mu_{0} N I}{2 \pi \rho}.\tag{5.41}\]

Vemos que un posible inconveniente de este sistema para aplicaciones prácticas es que el campo interno sí depende\(\ \rho\), es decir, no es del todo uniforme; sin embargo, si el toro es relativamente delgado, esta deficiencia es menor.

A continuación discutamos una cuestión muy importante: ¿cómo podemos resolver los problemas de la magnetostática para sistemas cuya baja simetría no permite obtener resultados fáciles de la ley Ampère? (Los ejemplos son, por supuesto, demasiado numerosos para enumerarlos; por ejemplo, no podemos usar este enfoque ni siquiera para reproducir la ecuación (23) para un bucle de corriente redondo.) A partir de la profunda analogía con la electrostática, podemos esperar que en este caso, podamos calcular el campo magnético resolviendo un cierto problema límite para el potencial del campo —en nuestro caso actual, el potencial vectorial\(\ \mathbf{A}\) definido por la Ec. (28). Sin embargo, a pesar de la similitud de esta fórmula y la Ec. (1.38) para\(\ \phi\), que se notó anteriormente, hay dos cuestiones adicionales que debemos abordar en la caja magnética.

Primero, calcular la distribución de potencial vectorial significa determinar tres funciones escalares (digamos,\(\ A_{x}, A_{y}\), y\(\ A_{z}\)), en lugar de una\(\ (\phi)\). Para revelar el segundo tema más profundo, conectemos la Ec. (27) a la Ec. (35):

\[\ \nabla \times(\nabla \times \mathbf{A})=\mu_{0} \mathbf{j},\tag{5.42}\]

y luego aplicar al lado izquierdo de esta ecuación la identidad ahora familiar (31). El resultado es

\[\ \nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{j}.\tag{5.43}\]

Por otro lado, como sabemos por electrostática (por favor compare las ecuaciones (1.38) y (1.41)), el potencial vectorial\(\ \mathbf{A}(\mathbf{r})\) dado por la ecuación (28) tiene que satisfacer una ecuación más simple (“vector-Poisson”)

\[\ \nabla^{2} \mathbf{A}=-\mu_{0} \mathbf{j},\quad\quad\quad\quad\text{Poisson equation for A}\tag{5.44}\]

que es solo un conjunto de tres ecuaciones habituales de Poisson para cada componente cartesiano de\(\ \text { A }\).

Para resolver la diferencia entre estos resultados, observemos que la Ec. (43) se reduce a la Ec. (44) si\(\ \nabla \cdot \mathbf{A}=0\). En este contexto, discutamos qué discrecionalidad tenemos en la elección del potencial. En electrostática, podríamos agregar a la función escalar\(\ \phi^{\prime}\) que satisfizo la Ec. (1.33) para el campo dado\(\ \mathbf{E}\), no solo una constante arbitraria sino incluso una función arbitraria del tiempo:

\[\ -\nabla\left[\phi^{\prime}+f(t)\right]=-\nabla \phi^{\prime}=\mathbf{E}.\tag{5.45}\]

Del mismo modo, usando el hecho de que curl del gradiente de cualquier función escalar es igual a cero, ¹⁸ podemos agregar a cualquier función vectorial\(\ \mathbf{A}^{\prime}\) que satisfaga la ecuación (27) para el campo dado\(\ \mathbf{B}\), no solo cualquier constante sino incluso un gradiente de una función escalar arbitraria\(\ \chi(\mathbf{r}, t)\), porque

\[\ \nabla \times\left(\mathbf{A}^{\prime}+\nabla \chi\right)=\nabla \times \mathbf{A}^{\prime}+\nabla \times(\nabla \chi)=\nabla \times \mathbf{A}^{\prime}=\mathbf{B}.\tag{5.46}\]

Tales adiciones, que mantienen intactos los campos, se denominan transformaciones de calibre. ¹⁹ Veamos qué hace tal transformación para\(\ \nabla \cdot \mathbf{A^{\prime}}\):

\[\ \nabla \cdot\left(\mathbf{A}^{\prime}+\nabla \chi\right)=\nabla \cdot \mathbf{A}^{\prime}+\nabla^{2} \chi.\tag{5.47}\]

Para cualquier elección de tal función\(\ \mathbf{A}^{\prime}\), siempre podemos elegir la función de tal\(\ \chi\) manera que satisfaga la ecuación de Poisson\(\ \nabla^{2} \chi=-\nabla \cdot \mathbf{A}^{\prime}\), y por lo tanto haga que la divergencia del potencial vectorial transformado,\(\ \mathbf{A}=\mathbf{A}^{\prime}+\nabla \chi\), igual a cero en todas partes,

\[\ \nabla \cdot \mathbf{A}=0,\quad\quad\quad\quad\text{Coulomb gauge}\tag{5.48}\]

reduciendo así la Ec. (43) a la Ec. (44).

En resumen, el conjunto de distribuciones\(\ \mathbf{A}^{\prime}(\mathbf{r})\) que satisfacen la Ec. (27) para un campo dado\(\ \mathbf{B}(\mathbf{r})\), no se limita al potencial vectorial\(\ \mathbf{A}(\mathbf{r})\) dado por la ecuación (44), sino que se reduce a él en la condición adicional del calibre de Coulomb (48). Sin embargo, como veremos en un minuto, incluso esta condición aún deja algunos grados de libertad en la elección del potencial vectorial. Para ilustrar este hecho, y también para tener una mejor idea de la distribución del potencial vectorial en el espacio, calculemos\(\ \mathbf{A}(\mathbf{r})\) para dos casos muy básicos.

Primero, reconsideremos el problema del cable recto que se muestra en la Fig. 5. Como muestra la Ec. (28), en este caso el potencial vectorial\(\ \mathbf{A}\) tiene solo un componente (a lo largo del eje\(\ z\)). Además, debido a la simetría axial del problema, su magnitud solo puede depender de la distancia desde el eje:\(\ \mathbf{A}=\mathbf{n}_{z} A(\rho)\). De ahí que el
gradiente de\(\ \mathbf{A}\) se dirija a través del eje z, de manera que la Ec. (48) se satisface en todos los puntos. Para nuestra simetría\(\ (\partial / \partial \varphi=\partial / \partial z=0)\), el operador Laplace, escrito en coordenadas cilíndricas, tiene solo un término, ²⁰ reduciendo la Eq. (44) a

\[\ \frac{1}{\rho} \frac{d}{d \rho}\left(\rho \frac{d A}{d \rho}\right)=-\mu_{0} j(\rho).\tag{5.49}\]

Multiplicando ambas partes de esta ecuación por\(\ \rho\) e integrándolas sobre la coordenada una vez, obtenemos

\[\ \rho \frac{d A}{d \rho}=-\mu_{0} \int_{0}^{\rho} j\left(\rho^{\prime}\right) \rho^{\prime} d \rho^{\prime}+\mathrm{const}.\tag{5.50}\]

Ya que en las coordenadas cilíndricas, para nuestra simetría\(\ B=-d A / d \rho\),, ²¹ Eq. (50) no es otra cosa que nuestro antiguo resultado (38) para el campo magnético. ²² Sin embargo, continuemos con la integración, al menos para la región fuera del cable, donde la función\(\ A(\rho)\) depende únicamente de la corriente completa en\(\ I\) lugar de la distribución de corriente. Dividiendo ambas partes de la ecuación (50) por\(\ \rho\), e integrándolas de nuevo sobre este argumento, obtenemos

\[\ A(\rho)=-\frac{\mu_{0} I}{2 \pi} \ln \rho+\mathrm{const}, \quad \text { where } I=2 \pi \int_{0}^{R} j(\rho) \rho d \rho, \quad \text { for } \rho \geq R.\tag{5.51}\]

Como recordatorio, tuvimos un comportamiento logarítmico similar para el potencial electrostático fuera de una línea recta uniformemente cargada. Esto es natural porque las ecuaciones de Poisson para ambos casos son similares.

Ahora encontremos el potencial vectorial para el solenoide largo (Fig. 6a), con su campo magnético uniforme. Dado que la Ec. (28) dice que el vector\(\ \mathbf{A}\) debe seguir la dirección de la corriente inductora, podemos comenzar por buscarlo en la forma\(\ \mathbf{A}=\mathbf{n}_{\varphi} A(\rho)\). (Esto es especialmente natural si la sección transversal del solenoide es circular). Con esta orientación de\(\ \mathbf{A}\), la misma expresión general para el operador de rizo en coordenadas cilíndricas rinde\(\ \nabla \times \mathbf{A}=\mathbf{n}_{z}(1 / \rho) d(\rho A) / d \rho\). De acuerdo con la Ec. (27), esta expresión debe ser igual a\(\ \mathbf{B}\) —en nuestro caso actual a\(\ \mathbf{n}_{z} B\), con una constante\(\ B\) — ver Ec. (40). Integrando esta igualdad, y seleccionando tal constante de integración que\(\ A(0)\) sea finita, obtenemos

\[\ A(\rho)=\frac{B\rho}{2},\quad\quad\quad\text { i.e. } \mathbf{A}=\frac{B \rho}{2} \mathbf{n}_{\varphi}.\tag{5.52}\]

Conectando este resultado a la expresión general para el operador Laplace en las coordenadas cilíndricas, ²³ vemos que la ecuación de Poisson (44) con\(\ \mathbf{j}=0\) (es decir, la ecuación de Laplace), se satisface de nuevo —lo cual es natural ya que, para esta distribución, el calibre de Coulomb condición (48) se satisface:\(\ \nabla \cdot \mathbf{A}=0\).

Sin embargo, la ecuación (52) no es el potencial de vector único (o incluso el más simple) que da el mismo campo uniforme\(\ \mathbf{B}=\mathbf{n}_{z} B\). De hecho, usando la expresión bien conocida para el operador curl en coordenadas cartesianas, ²⁴ es sencillo verificar que cada uno de los vectores funcione\(\ \mathbf{A}^{\prime}=\mathbf{n}_{y} B x\) y\(\ \mathbf{A}^{\prime \prime}=-\mathbf{n}_{x} B y\) también tenga el mismo curl, y también satisfaga la condición de calibre Coulomb (48). ²⁵ Si tales soluciones no parecen muy naturales por su anisotropía en el plano [x, y], por favor considere el hecho de que representan el campo magnético uniforme independientemente de su fuente —por ejemplo, independientemente de la forma de la sección transversal del solenoide largo. Tales elecciones del potencial vectorial pueden ser muy convenientes para algunos problemas, por ejemplo para el análisis cuántico-mecánico del movimiento 2D de una partícula cargada en el campo magnético perpendicular, dando los famosos niveles de energía Landau. ²⁶

---

Referencia

¹² En las unidades gaussianas, la Ec. (27) sigue siendo la misma, y por lo tanto en la Ec. (28),\(\ \mu_{0} / 4 \pi\) se sustituye por\(\ 1 / c\).

¹³ Véase, por ejemplo, MA Ec. (11.2).

¹⁴ Véase, por ejemplo, MA Eq. (11.3).

¹⁵ Como en todas las fórmulas anteriores para el campo magnético, en las unidades gaussianas, el coeficiente\(\ \mu_{0}\) en esta relación se sustituye por\(\ 4 \pi / c\).

¹⁶ Véase, por ejemplo, MA Ec. (12.1) con\(\ \mathbf{f}=\mathbf{B}\).

¹⁷ Aplicando la ley Ampère a un contorno circular de radio\(\ \rho\), coaxial con el solenoide, vemos que el campo afuera (¡pero no dentro!) tiene un componente azimutal\(\ B_{\varphi}\), similar al del cable recto (ver Ec. (38) anterior) y por lo tanto (at\(\ N >>1\)) mucho más débil que el campo longitudinal dentro del solenoide — ver Eq. (40).

¹⁸ Véase, por ejemplo, MA Ec. (11.1).

¹⁹ El uso del término “calibre” (que originalmente significa “una medida” o “una escala”) en este contexto es puramente histórico, por lo que el lector no debe tratar de encontrar demasiado sentido oculto en él.

²⁰ Véase, por ejemplo, MA Ec. (10.3).

²¹ Véase, por ejemplo, MA Ec. (10.5) con\(\ \partial / \partial \varphi=\partial / \partial z=0\).

²² Ya que el campo magnético en el eje del cable tiene que ser cero (de lo contrario, siendo normal al eje, ¿a dónde se dirigiría?) , la constante de integración en la Ec. (50) tiene que ser igual a cero.

²³ Véase, por ejemplo, MA Ec. (10.6).

²⁴ Véase, por ejemplo, MA Ec. (8.5).

²⁵ El potencial vectorial axialmente simétrico (52) es solo una suma ponderada de estas dos funciones:\(\ \mathbf{A}=\left(\mathbf{A}^{\prime}+\mathbf{A}^{\prime \prime}\right) / 2\).

²⁶ Véase, e.g., QM Sec. 3.2.