7.4: Refracción

Ahora consideremos los efectos que surgen en una interfaz plana entre dos medios uniformes si el ángulo de incidencia de la onda\(\ \theta\) (Fig. 10) es arbitrario, más que igual a cero como en nuestro análisis anterior, para el caso más simple de medios totalmente transparentes, con real\(\ \varepsilon_{\pm}(\omega)\) y\(\ \mu_{\pm}(\omega)\). (En aras de la simplicidad de la notación, se descartará el argumento de estas funciones, es decir, solo implícito en la mayoría de las fórmulas a continuación).

Fig. 7.10. Reflejo, transmisión y refracción de ondas planas en una interfaz plana. El plano del dibujo se selecciona para que contenga los tres vectores de onda:\(\ \mathbf{k}_{+}, \mathbf{k}_{-}\), y\(\ \mathbf{k}_{-}^{’}\).

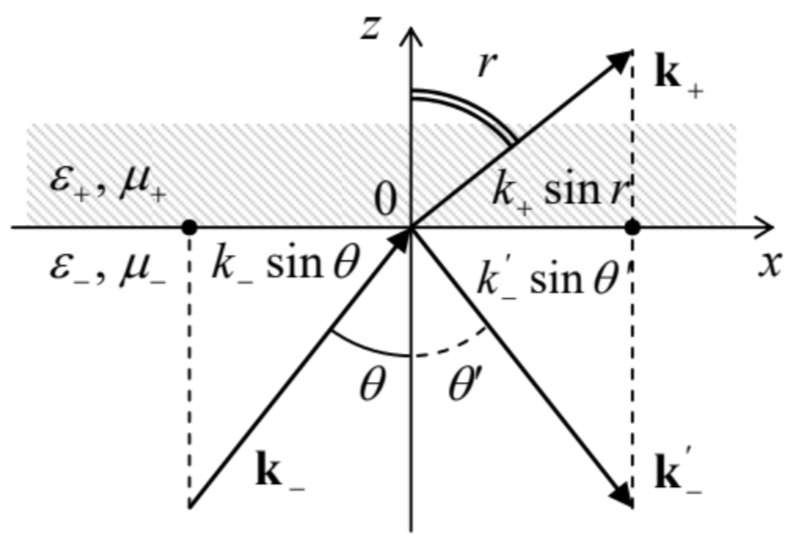
En contraste con el caso de incidencia normal, aquí los vectores de onda\(\ \mathbf{k}_{-}, \mathbf{k}_{-}^{\prime}\), y\(\ \mathbf{k}_{+}\) de los tres componentes (incidente, reflejada y transmitida) las ondas pueden tener diferentes direcciones. (Tal cambio en la dirección de la onda transmitida se llama refracción.) De ahí que comencemos nuestro análisis escribiendo una expresión general para un solo plano, onda monocromática para el caso en que su vector de onda k tenga los tres componentes cartesianos, en lugar de uno. Una generalización evidente de la Ec. (11) para este caso es

\[\ f(\mathbf{r}, t)=\operatorname{Re}\left[f_{\omega} e^{\left.i\left(k_{x} x+k_{y} y+k_{z} z\right)-\omega t\right)}\right] \equiv \operatorname{Re}\left[f_{\omega} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}\right].\tag{7.79}\]

Esta expresión permite un rápido análisis de las relaciones “cinemáticas” que son independientes de las impedancias mediáticas. En efecto, es suficiente notar que para satisfacer cualquier condición de límite lineal y homogénea en la interfaz (\(\ z = 0\)), todas las ondas planas parciales deben tener la misma dependencia temporal y espacial de este plano. De ahí que si seleccionamos el\(\ x-z\) plano para que el vector\(\ \mathbf{k}_{-}\) se encuentre en él\(\ \left(k_{-}\right)_{y}=0\), entonces,\(\ \mathbf{k}_{+}\) y tampoco\(\ \mathbf{k}^{\prime}_{-}\) puede tener ningún componente y, es decir, los tres vectores de onda se encuentran en el mismo plano —eso se selecciona como el plano del dibujo en la Fig. 10. Además, por la misma razón, sus componentes x deben ser iguales:

\[\ k_{-} \sin \theta=k_{-}^{\prime} \sin \theta^{\prime}=k_{+} \sin r.\tag{7.80}\]

De aquí obtenemos inmediatamente dos leyes bien conocidas: de la reflexión

\[\ \text{Reflection angle}\quad\quad\quad\quad \theta^{\prime}=\theta,\tag{7.81}\]

y refracción: ³³

\[\ \text{Snell law}\quad\quad\quad\quad\frac{\sin r}{\sin \theta}=\frac{k_{-}}{k_{+}}.\tag{7.82}\]

En esta forma, las leyes son válidas para ondas planas de cualquier naturaleza. En óptica, la ley Snell (82) se representa frecuentemente en la forma

\[\ \frac{\sin r}{\sin \theta}=\frac{n_{-}}{n_{+}},\tag{7.83}\]

donde\(\ n_{\pm}\) está el índice de refracción, también llamado “índice de refracción” del medio correspondiente, definido como su número de onda normalizado al del espacio libre (a la frecuencia de la onda particular):

\[\ \text{Index of refraction}\quad\quad\quad\quad n_{\pm} \equiv \frac{k_{\pm}}{k_{0}} \equiv\left(\frac{\varepsilon_{\pm} \mu_{\pm}}{\varepsilon_{0} \mu_{0}}\right)^{1 / 2}.\tag{7.84}\]

Quizás el corolario más famoso de la ley Snell es que si una ola se propaga desde un medio con un índice de refracción superior a aquel con uno inferior (es decir, si\(\ n_{-}>n_{+}\) en la Fig. 10), por ejemplo del agua al aire, siempre hay cierto valor crítico\(\ \theta_{\mathrm{c}}\) del ángulo de incidencia,

\[\ \text{Critical angle}\quad\quad\quad\quad \theta_{c}=\sin ^{-1} \frac{n_{+}}{n_{-}} \equiv \sin ^{-1}\left(\frac{\varepsilon_{+} \mu_{+}}{\varepsilon_{-} \mu_{-}}\right)^{1 / 2},\tag{7.85}\]

a la que alcanza el ángulo de refracción r (ver Fig. 10 nuevamente)\(\ \pi / 2\). A una mayor\(\ \theta\), es decir, dentro del rango\(\ \theta_{\mathrm{c}}<\theta<\pi/2\), las condiciones límite (80) no pueden ser satisfechas por una onda refractada con un vector de onda real, de manera que la onda experimenta la llamada reflexión interna total. Este efecto es muy importante para la práctica, ya que significa que las superficies dieléctricas pueden ser utilizadas como espejos ópticos, en particular en fibras ópticas, para ser discutidas con más detalle en la Sec. 7 a continuación. Esto es muy afortunado para la tecnología de telecomunicaciones, porque el reflejo de la luz de los metales es bastante imperfecto. De hecho, según la Ec. (78), en el rango óptico\(\ \left(\lambda_{0} \sim 0.5 \mu \mathrm{m} \text {, i.e. } \omega \sim 10^{15} \mathrm{~s}^{-1}\right)\), incluso los mejores conductores (con\(\ \sigma \sim 6 \times 10^{8} \mathrm{~S} / \mathrm{m}\) y por lo tanto la profundidad normal de la piel\(\ \delta_{\mathrm{s}} \sim 1.5 \mathrm{~nm}\)) proporcionan una pérdida de potencia de al menos un pequeño porcentaje en cada reflexión.

Obsérvese, sin embargo\(\ \theta_{\mathrm{c}}<\theta<\pi / 2\), que incluso dentro del rango\(\ z>0\), el campo at, no es idénticamente igual a cero: penetra en los medios menos densos por una distancia del orden de\(\ \lambda_{0}\), descomponiéndose exponencialmente en su interior, tal como lo hace en la incidencia normal — ver Fig. 8. Sin embargo, en\(\ \theta \neq 0\) el campo penetrante todavía se propaga, con el número de onda (80), a lo largo de la interfaz. Tal campo, que cae exponencialmente en una dirección pero que aún se propaga como una onda en otra dirección, comúnmente se llama la onda evanescente.

Una observación más: así como en la incidencia normal, la penetración del campo en otro medio provoca un desplazamiento de fase de la onda reflejada — véase, por ejemplo, la Ec. (69) y su discusión. Una nueva característica de este cambio de fase, que surge en\(\ \theta \neq 0\), es que también tiene un componente paralelo a la interfaz —el llamado efecto Goos- Hänchen. En óptica geométrica, este efecto conduce a un desplazamiento de imagen (relativo a que su posición en un espejo perfecto) con componentes tanto normales como paralelos a la interfaz.

Ahora hagamos un análisis de las relaciones “dinámicas” que determinan las amplitudes de las ondas refractadas y reflejadas. Para esto, necesitamos escribir explícitamente las condiciones de contorno en la interfaz (es decir, el plano\(\ z=0\)). Dado que ahora los campos eléctricos y/o magnéticos pueden tener componentes normales al plano, además de la continuidad de sus componentes tangenciales, los cuales fueron discutidos repetidamente anteriormente,

\[\ \left.E_{x, y}\right|_{z=-0}=\left.E_{x, y}\right|_{z=+0},\left.\quad H_{x, y}\right|_{z=-0}=\left.H_{x, y}\right|_{z=+0},\tag{7.86}\]

también necesitamos relaciones para los componentes normales. Como se desprende de las ecuaciones macroscópicas homogéneas de Maxwell (6.99b), también son las mismas que en la estática, es decir\(\ D_{n}=\mathrm{const}\), y\(\ B_{n}=\mathrm{const}\), para nuestra elección de coordenadas (Fig. 10) dando

\[\ \left.\varepsilon_{-} E_{z}\right|_{z=-0}=\left.\varepsilon_{+} E_{z}\right|_{z=+0},\left.\quad \mu_{-} H_{z}\right|_{z=-0}=\left.\mu_{+} H_{z}\right|_{z=+0}.\tag{7.87}\]

Las expresiones de estos componentes a través de las amplitudes\(\ E_{\omega}\)\(\ R E_{\omega}\), y\(\ T E_{\omega}\) de las ondas incidentes, reflejadas y transmitidas dependen de la polarización de la onda incidente. Por ejemplo, para una onda linealmente polarizada con el vector de campo eléctrico perpendicular al plano de incidencia, es decir, paralela al plano de la interfaz, las ondas reflejadas y refractadas están polarizadas de manera similar — ver Fig. 11a.

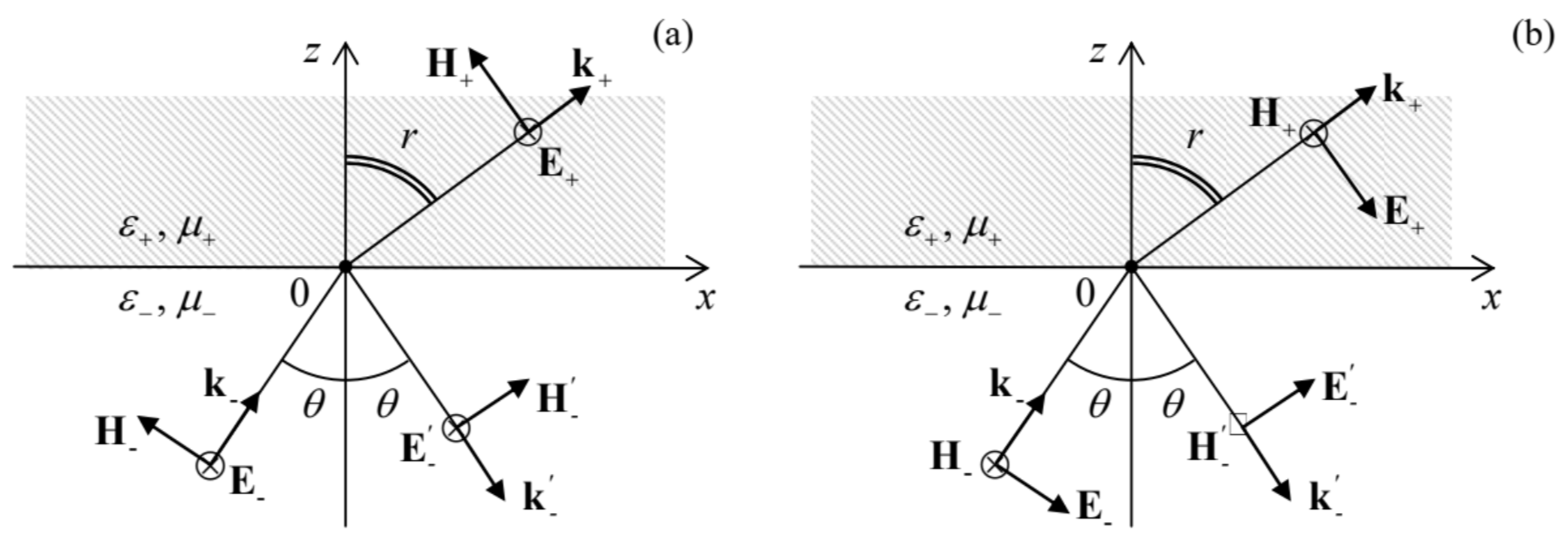Fig. 7.11. Reflexión y refracción a dos polarizaciones lineales diferentes de la onda incidente.

Como resultado, todos\(\ E_{z}\) son iguales a cero (de manera que la primera de las ecuaciones (87) es intrascendente), mientras que los componentes tangenciales del campo eléctrico son iguales a sus amplitudes completas, al igual que en la incidencia normal, por lo que todavía podemos usar ecuaciones (64) expresando estos componentes a través de los coeficientes\(\ R\) y\(\ T\). Sin embargo, en\(\ \theta \neq 0\) los campos magnéticos no sólo tienen componentes tangenciales

\[\ \left.H_{x}\right|_{z=-0}=\operatorname{Re}\left[\frac{E_{\omega}}{Z_{-}}(1-R) \cos \theta e^{-i \omega t}\right],\left.\quad H_{x}\right|_{z=+0}=\operatorname{Re}\left[\frac{E_{\omega}}{Z_{+}} T \cos r e^{-i \omega t}\right],\tag{7.88}\]

sino también componentes normales (ver Fig. 11a):

\[\ \left.H_{z}\right|_{z=-0}=\operatorname{Re}\left[\frac{E_{\omega}}{Z_{-}}(1+R) \sin \theta e^{-i \omega t}\right],\left.\quad H_{z}\right|_{z=+0}=\operatorname{Re}\left[\frac{E_{\omega}}{Z_{+}} T \sin r e^{-i \omega t}\right].\tag{7.89}\]

Conectando estas expresiones a las condiciones de límite expresadas por las ecuaciones (86) (en este caso, solo para los componentes y) y la segunda de las ecuaciones (87), obtenemos tres ecuaciones para dos coeficientes desconocidos\(\ R\) y\(\ T\). Sin embargo, dos de estas ecuaciones se duplican entre sí debido a la ley de Snell, y obtenemos solo dos ecuaciones independientes,

\[\ 1+R=T, \quad \frac{1}{Z_{-}}(1-R) \cos \theta=\frac{1}{Z_{+}} T \cos r,\tag{7.90}\]

que son una generalización muy natural de las ecuaciones (67), con los reemplazos\(\ Z_{-} \rightarrow Z_{-} \cos r, Z_{+} \rightarrow Z_{+} \cos \theta\). Como resultado, podemos usar inmediatamente la Eq. (68) para escribir la solución del sistema (90): ³⁴

\[\ R=\frac{Z_{+} \cos \theta-Z_{-} \cos r}{Z_{+} \cos \theta+Z_{-} \cos r}, \quad T=\frac{2 Z_{+} \cos \theta}{Z_{+} \cos \theta+Z_{-} \cos r}.\tag{7.91a}\]

Si queremos expresar estos coeficientes solo a través del ángulo de incidencia, debemos usar la ley Snell (82) para eliminar el ángulo r, obteniendo las expresiones más voluminosas de uso común:

\[\ R=\frac{Z_{+} \cos \theta-Z_{-}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}}{Z_{+} \cos \theta+Z_{-}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}}, \quad T=\frac{2 Z_{+} \cos \theta}{Z_{+} \cos \theta+Z_{-}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}}.\tag{7.91b}\]

Sin embargo, mi preferencia personal es usar la relación cinemática (82) y las relaciones dinámicas (91a) por separado, porque la ecuación (91b) oscurece el hecho físico muy importante de que y la relación de\(\ k_{\pm}\), es decir, de las velocidades de onda de los dos medios, solo está involucrada en la ley Snell, mientras que la dinámica las relaciones esencialmente incluyen solo la relación de impedancias de onda, al igual que en el caso de la incidencia normal.

En el caso contrario de la polarización lineal del campo eléctrico dentro del plano de incidencia (Fig. 11b), es el campo magnético el que no tiene un componente normal, por lo que ahora es el segundo de las ecuaciones (87) el que no participa en la solución. Sin embargo, ahora los campos eléctricos en dos medios tienen no sólo componentes tangenciales,

\[\ \left.E_{x}\right|_{z=-0}=\operatorname{Re}\left[E_{\omega}(1+R) \cos \theta e^{-i \omega t}\right],\left.\quad E_{x}\right|_{z=+0}=\operatorname{Re}\left[E_{\omega} T \cos r e^{-i \omega t}\right],\tag{7.92}\]

sino también componentes normales (Fig. 11b):

\[\ \left.E_{z}\right|_{z=-0}=E_{\omega}(-1+R) \sin \theta,\left.\quad E_{z}\right|_{z=+0}=-E_{\omega} T \sin r.\tag{7.93}\]

Como resultado, en lugar de las ecuaciones (90), los coeficientes de reflexión y transmisión se relacionan como

\[\ (1+R) \cos \theta=T \cos r, \quad \frac{1}{Z_{-}}(1-R)=\frac{1}{Z_{+}} T.\tag{7.94}\]

Nuevamente, la solución de este sistema puede escribirse inmediatamente usando la analogía con la Ec. (67):

\[\ R=\frac{Z_{+} \cos r-Z_{-} \cos \theta}{Z_{+} \cos r+Z_{-} \cos \theta}, \quad T=\frac{2 Z_{+} \cos \theta}{Z_{+} \cos r+Z_{-} \cos \theta},\tag{7.95a}\]

o, alternativamente, utilizando la ley Snell, en una forma más voluminosa:

\[\ R=\frac{Z_{+}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}-Z_{-} \cos \theta}{Z_{+}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}+Z_{-} \cos \theta}, \quad T=\frac{2 Z_{+} \cos \theta}{Z_{+}\left[1-\left(k_{-} / k_{+}\right)^{2} \sin ^{2} \theta\right]^{1 / 2}+Z_{-} \cos \theta}.\tag{7.95b}\]

Para el caso particular\(\ \mu_{+}=\mu_{-}=\mu_{0}\), cuando\(\ Z_{+} / Z_{-}=\left(\varepsilon_{-} / \varepsilon_{+}\right)^{1 / 2}=k_{-} / k_{+}=n_{-} / n_{+}\) (que es aproximadamente correcto para los medios ópticos tradicionales), las ecuaciones (91b) y (95b) se denominan fórmulas de Fresnel. ³⁵ La mayoría de los libros de texto son rápidos en señalar que existe una diferencia importante entre ellos: mientras que para la polarización del campo eléctrico dentro del plano de incidencia (Fig. 11b), la amplitud de la onda reflejada (proporcional al coeficiente\(\ R\)) se vuelve a cero ³⁶ a un valor especial de\(\ \theta\) (llamado el ángulo Brewster): ³⁷

\[\ \theta_{\mathrm{B}}=\tan ^{-1} \frac{n_{+}}{n_{-}},\tag{7.96}\]

mientras que no existe tal ángulo en el caso opuesto (mostrado en la Fig. 11a). No obstante, tenga en cuenta que esta afirmación, así como la Ec. (96), es cierta sólo para el caso\(\ \mu_{+}=\mu_{-}\). En el caso general de diferentes\(\ \varepsilon\) y\(\ \mu\), Eq. (91) y (95) muestran que la onda reflejada se desvanece en\(\ \theta=\theta_{\mathrm{B}}\) con

\ [\\ tan ^ {2}\ theta_ {\ mathrm {B}} =\ frac {\ varepsilon_ {-}\ mu_ {+} -\ varepsilon_ {+}\ mu_ {-}} {\ varepsilon_ {+}\ mu_ {+} -\ varepsilon_ {-}\ mu_}}\ times\ left\ {\ begin {array} {cl}
\ left (\ mu_ {+}/\ mu_ {-}\ right), &\ text {for}\ mathbf {E}\ perp\ mathbf {n} _ {z}\ text {(Fig.11a)}\\
\ left (-\ varepsilon_ {+}/\ varepsilon_ {-}\ derecha), &\ text {for}\ mathbf {H}\ perp\ mathbf {n} _ {z}\ text {(Fig. 11b)}
\ end {array}\ right. \ quad\ quad\ quad\ quad\ text {ángulo Brewster}\ tag {7.97}\]

Obsérvese la\(\ \varepsilon \leftrightarrow \mu\) simetría natural de estas relaciones, resultante de la\(\ \mathbf{E} \leftrightarrow \mathbf{H}\) simetría para estos dos casos de polarización (Fig. 11). Estas fórmulas también muestran que para cualquier conjunto de parámetros de los dos medios (con\(\ \varepsilon_{\pm}, \mu_{\pm}>0\)),\(\ \tan ^{2} \theta_{\mathrm{B}}\) es positivo (y por lo tanto\(\ \theta_{\mathrm{B}}\) existe un ángulo Brewster real) solo para una de estas dos polarizaciones. En particular, si la interfaz se debe al cambio de\(\ \mu\) solo (es decir, if\(\ \varepsilon_{+}=\varepsilon_{-}\)), la primera de las Eqs. (97) se reduce nuevamente a la forma simple (96), mientras que para la polarización mostrada en la Fig. 11b no hay ángulo Brewster, es decir, la onda reflejada tiene una amplitud distinta de cero para cualquiera\(\ \theta\).

Tal relato de ambos parámetros mediáticos,\(\ \varepsilon\) y\(\ \mu\), en igualdad de condiciones, es necesario describir los llamados efectos de refracción negativos. ³⁸ Como se mostró en la Sec. 2, en un medio con resonancias impulsadas por campo eléctrico, la función\(\ \varepsilon(\omega)\) puede ser casi real y negativa, al menos dentro de
intervalos de frecuencia limitados — ver, en particular, la Ec. (34) y la Fig. 5. Como ya se ha comentado, si, a estas frecuencias, la función\(\ \mu(\omega)\) es real y positiva, entonces\(\ k^{2}(\omega)=\omega^{2} \varepsilon(\omega) \mu(\omega)<0\), y\(\ k\) puede representarse como\(\ i / \delta\) con un real\(\ \delta\), es decir, el campo exponencial decaimiento en el medio. Sin embargo, consideremos el caso cuando ambos\(\ \varepsilon(\omega)<0\) y\(\ \mu(\omega)<0\) con cierta frecuencia. (Esto es posible en un medio con resonancias impulsadas por E y accionadas por H, a una elección adecuada de sus frecuencias de resonancia). Ya que en este caso\(\ k^2(\omega)=\omega^{2} \varepsilon(\omega) \mu(\omega)>0\), el vector de onda es real, por lo que la Ec. (79) describe una ola viajera, y se podría pensar que no hay nada nuevo en este caso. ¡No es así!

En primer lugar, para una onda sinusoidal, plana (79), el operador\(\ \nabla\) es equivalente a la multiplicación por\(\ i \mathbf{k}\). Como muestran las ecuaciones de Maxwell (2a), esto significa que en una dirección fija de los vectores E y k, la inversión simultánea de los signos de\(\ \varepsilon\) y\(\ \mu\) significa la inversión de la dirección del vector H. Es decir, si ambas\(\ \varepsilon\) y\(\ \mu\) son positivas, estas ecuaciones se satisfacen con vectores mutuamente ortogonales {E, H, k} que forman el sistema habitual de la derecha (ver Fig. 1 y Fig. 12a), cuyo nombre deriva de la popular “regla de la derecha” utilizada para determinar la dirección del producto vectorial. Sin embargo, si ambos\(\ \varepsilon\) y\(\ \mu\) son negativos, los vectores forman un sistema a la izquierda — ver Fig. 12b. (Debido a este hecho, los medios de comunicación con\(\ \varepsilon<0\) y con frecuencia\(\ \mu<0\) se les llama los materiales zurdos, LHM para abreviar.) De acuerdo con la relación básica (6.114), que no involucra parámetros de medios, esto significa que para una onda plana en un material de la izquierda, el vector Poynting\(\ \mathbf{S}=\mathbf{E} \times \mathbf{H}\), es decir, el flujo de energía, se dirige opuesto al vector de onda k.

Fig. 7.12. Direcciones de los vectores principales de una onda plana dentro de un medio con (a) valores positivos y (b) negativos de\(\ \varepsilon\) y\(\ \mu\).

Este hecho puede parecer extraño, pero no está en contradicción con ningún principio fundamental. Permítanme recordarles que, según la definición del vector k, su dirección muestra la dirección de la velocidad de fase\(\ \nu_{\mathrm{ph}}=\omega / k\) de una onda sinusoidal (y por lo tanto infinitamente larga), que no puede ser utilizada, por ejemplo, para la señalización. Dicha señalización (mediante el envío de paquetes de onda — ver Fig. 13) es posible solo con la velocidad de grupo\(\ \nu_{\mathrm{gr}}=d \omega / d k\). Esta velocidad en los materiales de la izquierda es siempre positiva (dirigida a lo largo del vector S).

Fig. 7.13. Un ejemplo de un paquete de ondas que se mueve a lo largo del eje\(\ z\) con una velocidad de fase negativa, pero velocidad de grupo positiva. Las líneas azules muestran la instantánea de un paquete un intervalo de tiempo corto después de la primera instantánea (líneas rojas).

Quizás el efecto más fascinante posible con los materiales de la izquierda es la refracción ondulada en sus interfaces con los materiales diestros habituales, predichos por primera vez por V. Veselago en 1960. Consideremos el ejemplo mostrado en la Fig. 14a. En la onda incidente, llegando de un material habitual, las direcciones de los vectores\(\ \mathbf{k_{-}}\) y\(\ \mathbf{S_{-}}\) coinciden, y así están en la onda reflejada con vectores\(\ \mathbf{k_{-}^{\prime}}\) y\(\ \mathbf{S_{-}^{\prime}}\). Esto significa que los campos eléctricos y magnéticos en el plano de la interfaz\(\ (z = 0)\) son, a nuestra elección de coordenadas, proporcionales a\(\ \exp \left\{i k_{x} x\right\}\), con un componente positivo\(\ k_{x}=k_{-} \cos \theta\). Para satisfacer cualquier condición de límite lineal, la onda refractada, que se propaga en el material zurdo, tiene que coincidir con esa dependencia, es decir, tener un componente x positivo de su vector de onda\(\ \mathbf{k_{+}}\). Pero en este medio, este vector tiene que ser antiparalelo al vector\(\ \mathbf{S}\), que a su vez debería ser dirigido fuera de la interfaz, porque representa el flujo de potencia desde la interfaz hacia el grueso del material. Estas condiciones no pueden ser reconciliadas por la onda refractada que se propaga a lo largo de la dirección habitual de la ley Snell (mostrada con la línea discontinua en la figura 13a), sino que todas se satisfacen en la refracción en la dirección dada por el ángulo de Snell con el signo opuesto. (De ahí el término “refracción negativa”). ³⁹

Fig. 7.14. Refracción negativa: (a) ondas en la interfaz entre medios con valores positivos y negativos de\(\ \varepsilon \mu\), y (b) la lente perfecta hipotética: una placa paralela hecha de un material con\(\ \varepsilon=-\varepsilon_{0}\) y\(\ \mu=-\mu_{0}\).

Para entender cuán inusuales pueden ser los resultados de la refracción negativa, consideremos una losa paralela de espesor\(\ d\), hecha de un hipotético material zurdo con valores exactamente seleccionados\(\ \varepsilon=-\varepsilon_{0}\), y\(\ \mu=-\mu_{0}\) (ver Fig. 14b). Para tal material, colocado en el espacio libre, el ángulo de refracción\(\ r=-\theta\), de manera que los rayos de una fuente puntual, ubicada en el espacio libre, a una\(\ a<d\) distancia de la losa, se propaguen como se muestra en ese panel, es decir, todos se encuentran de nuevo a la distancia a dentro de la placa, y luego continúan propagándose a la segunda superficie de la losa. Repitiendo nuestra discusión para esta superficie, vemos que la imagen de un punto también se forma más allá de la losa, a\(\ 2 a+2 b=2 a+2(d-a)=2 d\) distancia del objeto.

Superficialmente, este sistema parece una lente habitual, pero la conocida fórmula de lente, que relaciona\(\ a\) y\(\ b\) con la distancia focal\(\ f\), no está satisfecha. (En particular, un haz paralelo no se enfoca en un punto a ninguna distancia finita). Como diferencia adicional con respecto a la lente habitual, el sistema mostrado en la Fig. 14b no refleja ninguna parte de la luz incidente. En efecto, es sencillo verificar que para todas las fórmulas anteriores para\(\ R\) y\(\ T\) para que sean válidas, el signo de la impedancia de onda\(\ Z\) en los materiales zurdos tiene que mantenerse positivo. Así, para nuestra elección particular de parámetros\(\ \left(\varepsilon=-\varepsilon_{0}, \mu=-\mu_{0}\right)\), las ecuaciones (91a) y (95a) son válidas con\(\ Z_{+}=Z_{-}=Z_{0}\) y\(\ \cos r=\cos \theta=1\), dando\(\ R = 0\) para cualquier polarización lineal, y por lo tanto para cualquier otra polarización de onda: circular, elíptica, natural, etc.

La sugerencia de lente perfecta ha desencadenado una ola de esfuerzos para implementar materiales de la izquierda experimentalmente. (Los intentos de encontrar tales materiales en la naturaleza han fracasado hasta el momento). La mayor parte del avance en esta dirección se ha logrado utilizando los llamados metamateriales, que son esencialmente matrices cuasi-periódicas de resonadores electromagnéticos especialmente diseñados, idealmente con alta densidad\(\ n >> \lambda^{-3}\). Por ejemplo, la Fig. 15 muestra el metamaterial que se utilizó para la primera demostración de refractividad negativa en la región de microondas —para frecuencias de ~10-GHz. ⁴⁰ Combina tiras rectas de una película metálica, trabajando como resonadores agrupados con un gran momento dipolo eléctrico (por lo tanto fuertemente acoplado al campo eléctrico de la onda E), y varios bucles de película casi cerrados (los llamados anillos divididos), trabajando como resonadores agrupados con grandes momentos dipolares magnéticos, acoplados al campo H. La refractividad negativa se logra diseñando las frecuencias de resonancia cercanas entre sí. Más recientemente, los metamateriales con refractividad negativa se demostraron en el rango óptico, ⁴¹ aunque a lo mejor de mi conocimiento, su absorción relativamente grande aún impide aplicaciones prácticas.

Fig. 7.15. Un material artificial de la izquierda que proporciona refracción negativa a frecuencias de microondas ~10 GHz. El original de Jeffrey D. Wilson (de dominio público) está disponible en https://en.Wikipedia.org/wiki/Metamaterial.

Este progreso ha estimulado el desarrollo de otros usos potenciales de los metamateriales (no necesariamente los zurdos), en particular, diseños de sistemas no uniformes con distribuciones diseñadas\(\ \varepsilon(\mathbf{r}, \omega)\) y\(\ \mu(\mathbf{r}, \omega)\) que pueden proporcionar propagación de ondas electromagnéticas a lo largo de las trayectorias deseadas, p. alrededor de cierta región del espacio, haciéndola prácticamente invisible para un observador externo, hasta ahora, dentro de un rango de frecuencia limitado. ⁴²

Como se mencionó en la Sec. 5.5, otra forma de alcanzar valores negativos de\(\ \mu(\omega)\) es colocar un material ferromagnético en un campo magnético de CC externo tal que la frecuencia\(\ \omega_{\mathrm{r}}\) de la resonancia ferromagnética sea algo menor que\(\ \omega\). Si capas delgadas de dicho material (por ejemplo, níquel) se intercalan con
capas de un conductor no magnético muy bueno (como el cobre), el metamaterial resultante tiene un valor promedio de\(\ \mu(\omega)\), digamos, positivo, pero sustancialmente por debajo\(\ \mu_{0}\). De acuerdo con la Ec. (6.33), la profundidad\(\ \delta_{\mathrm{s}}\) de la piel de dicho material puede ser mayor que la del conductor bueno solo, lo que impone una distribución más uniforme de la corriente de CA que fluye a lo largo de las capas y, por lo tanto, hace que las pérdidas de energía sean más bajas que en el conductor bueno solo. Este efecto puede ser útil, en particular, para interconexiones de circuitos electrónicos. ⁴³

---

Referencia

³³ Esta última relación se llama tradicionalmente la ley Snell, después de un\(\ 17^{\text {th }}\) siglo astrónomo Willebrord Snelio, pero se remonta a una obra de alrededor del 984 de Abu Saad al-Ala ibn Sahl. (Claudio Ptolomeo que realizó experimentos pioneros sobre la refracción de la luz en el\(\ 2^{\text {nd }}\) siglo d.C., estaba a solo un paso de este resultado.)

³⁴ Obsérvese que podemos calcular los coeficientes de reflexión\(\ R^{\prime}\) y transmisión y\(\ T^{\prime}\) para la onda que viaja en la dirección opuesta con solo hacer los siguientes intercambios de parámetros:\(\ Z_{+} \leftrightarrow Z_{-}\) y\(\ \theta \leftrightarrow r\), y que los coeficientes resultantes satisfacen los siguientes Stokes relaciones:\(\ R^{\prime}=-R\), y\(\ R^{2}+T T^{\prime}=1\), para cualquier\(\ \mathrm{Z}_{\pm}\).

³⁵ El nombre de Augustin-Jean Fresnel (1788-1827), uno de los pioneros de la óptica de onda, a quien se le atribuye, entre muchas otras contribuciones (ver, en particular, las discusiones en el capítulo 8), por el concepto de luz como onda puramente transversal.

³⁶ Este efecto se utiliza en la práctica para obtener luz linealmente polarizada, con el vector de campo eléctrico perpendicular al plano de incidencia, a partir de la luz natural con su polarización aleatoria. Una aplicación aún más práctica del efecto es una reducción parcial del deslumbramiento indeseable de las superficies mojadas (para la interfaz agua/aire,\(\ n_{+} / n_{-} \approx 1.33\), dando\(\ \theta_{\mathrm{B}} \approx 50^{\circ}\)) mediante la fabricación de cubiertas de faros de automóviles y vidrios de materiales polarizantes verticales.

³⁷ Una interpretación muy sencilla de la ecuación (96) se basa en el hecho de que, junto con la ley Snell (82), da\(\ r+\theta=\pi/2\). Como resultado, el vector\(\ \mathbf{E}_{+}\) es paralelo al vector\(\ \mathbf{k}_{-}^{\prime}\), y por lo tanto, los dipolos eléctricos oscilantes del medio en\(\ z>0\) no tienen la componente que podría inducir el campo eléctrico transversal\(\ \mathbf{E}_{-}^{\prime}\) de la onda potencial reflejada.

³⁸ A pesar de algunos antecedentes importantes de trabajo teórico de A. Schuster (1904), L. Mandelstam (1945), D. Sivikhin (1957), y especialmente V. Veselago (1966-67), los efectos negativos de refractividad se convirtieron en un tema de investigación científica intensiva y desarrollo de ingeniería solo en la década de 2000. Tenga en cuenta que estos efectos no están cubiertos en los cursos típicos de E&M, por lo que el saldo de esta sección puede omitirse en primera lectura.

³⁹ En algunas publicaciones inspiradas en este hecho, a los materiales de la izquierda se les prescribe un índice negativo de refracción\(\ n\). Sin embargo, esta prescripción debe ser tratada con cuidado. Por ejemplo, cumple con la primera forma de la Ec. (84), pero no su segunda forma, y el signo de\(\ n\), en contraste con el del vector onda k, es cuestión de convención.

⁴⁰ R. Shelby et al., Science 292, 77 (2001); J. Wilson y Z. Schwartz, Appl. Phys. A lett. 86, 021113 (2005).

⁴¹ Véase, por ejemplo, J. Valentine et al., Nature 455, 376 (2008).

⁴² Para una revisión de tales “capas de invisibilidad”, véase, e.g., B. Wood, Comptes Rendus Physique 10, 379 (2009).

⁴³ Véase, por ejemplo, N. Sato et al., J. Appl. Phys. 111, 07A501 (2012), y sus referencias.