7.5: Presión Debido al Peso del Fluido
- Page ID
- 133798
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Definir la presión en términos de peso.
- Explicar la variación de la presión con la profundidad en un fluido.
- Calcular densidad dada la presión y altitud.
Si alguna vez te han hecho estallar las orejas en un vuelo de avión o te han dolorido durante una inmersión profunda en una piscina, has experimentado el efecto de la profundidad sobre la presión en un fluido. En la superficie de la Tierra, la presión del aire que se ejerce sobre ti es resultado del peso del aire por encima de ti. Esta presión se reduce a medida que subes en altitud y el peso del aire por encima de ti disminuye. Bajo el agua, la presión que se ejerce sobre ti aumenta con el aumento de la profundidad. En este caso, la presión que se ejerce sobre ti es resultado tanto del peso del agua por encima de ti como del de la atmósfera por encima de ti. Es posible que note un cambio de presión de aire en un viaje en ascensor que le transporta muchas historias, pero solo necesita bucear un metro más o menos debajo de la superficie de una piscina para sentir un aumento de presión. La diferencia es que el agua es mucho más densa que el aire, unas 775 veces más densa.
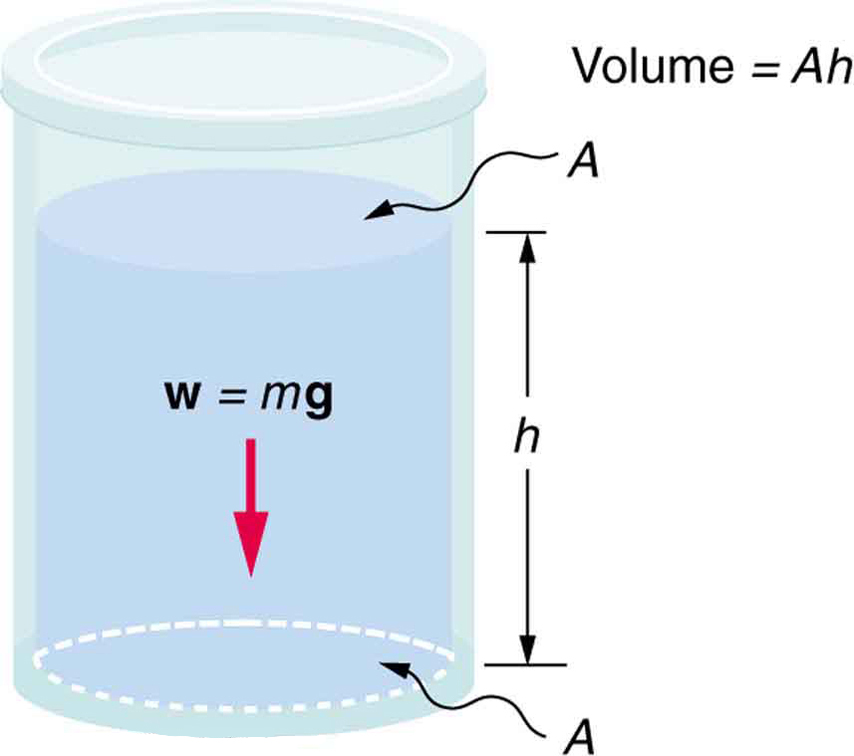
Considera el contenedor en la Figura\(\PageIndex{1}\). Su fondo soporta el peso del fluido que contiene. Calculemos la presión ejercida sobre el fondo por el peso del fluido. Esa presión es el peso del fluido\(mg\) dividido por el área que lo\(A\) soporta (el área del fondo del contenedor):
\[P=\frac{m g}{A}. \nonumber \]
Podemos encontrar la masa del fluido a partir de su volumen y densidad:
\[m=\rho V. \nonumber \]
El volumen del fluido\(V\) está relacionado con las dimensiones del contenedor. Es
\[V=A h, \nonumber \]
donde\(A\) es el área de la sección transversal y\(h\) es la profundidad. Combinando las dos últimas ecuaciones da
\[m=\rho A h. \nonumber \]
Si entramos esto en la expresión de presión, obtenemos
\[P=\frac{(\rho A h) g}{A}. \nonumber \]
El área cancela y reordenando las variables rinde
\[P=\rho g h. \nonumber \]
Este valor es la presión debida al peso de un fluido. La ecuación tiene validez general más allá de las condiciones especiales bajo las cuales se deriva aquí. Aunque el recipiente no estuviera ahí, el fluido circundante seguiría ejerciendo esta presión, manteniendo el fluido estático. Así, la ecuación\(P=\rho g h\) representa la presión debida al peso de cualquier fluido de densidad promedio\(\rho\) a cualquier profundidad\(h\) por debajo de su superficie. Para los líquidos, que son casi incompresibles, esta ecuación se mantiene a grandes profundidades.
Ejemplo\(\PageIndex{1}\): Calculating the Average Pressure and Force Exerted: What Force Must a Dam Withstand?
En el Ejemplo 8.2.1, calculamos la masa de agua en un reservorio grande. Consideraremos ahora la presión y la fuerza que actúa sobre la presa reteniendo el agua. (Ver Figura\(\PageIndex{2}\).) La presa tiene 500 m de ancho y el agua tiene 80,0 m de profundidad en la presa. a) ¿Cuál es la presión promedio sobre la presa debido al agua? (b) Calcular la fuerza ejercida contra la presa y compararla con el peso del agua en la presa (previamente encontrada que era 1.96×1013N).
Estrategia para: a
La presión promedio\(\overline{P}\) debida al peso del agua es la presión a la profundidad promedio\(\bar{h}\) de 40.0 m, ya que la presión aumenta linealmente con la profundidad.
Solución para (a)
La presión promedio debida al peso de un fluido es
\[\overline{P}=\rho g \bar{h}. \nonumber\]
Entrando a la densidad del agua de la Tabla 8.2.1 y tomando\(\bar{h}\) como profundidad promedio de 40.0 m, obtenemos
\ [\ begin {alineado}
\ overline {P} &=\ izquierda (10^ {3}\ frac {\ mathrm {kg}} {\ mathrm {m} ^ {3}}\ derecha)\ izquierda (9.80\ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}}\ derecha) (40.0\ mathrm {~m})\\
=3.92\ times 10^ {5}\ frac {\ mathrm {N}} {\ mathrm {m} ^ {2}} =392\ mathrm {kPa}.
\ end {alineado}\ nonumber\]
Estrategia para b
La fuerza ejercida sobre la presa por el agua es la presión promedio multiplicada por el área de contacto:
\[F=\overline{P} A \nonumber\]
Solución para (b)
Ya hemos encontrado el valor para\(\overline{P}\). El área de la presa es\(A=80.0 \mathrm{~m} \times 500 \mathrm{~m}=4.00 \times 10^{4} \mathrm{~m}^{2}\), de manera que
\ [\ begin {aligned}
F &=\ left (3.92\ times 10^ {5}\ mathrm {~N}/\ mathrm {m} ^ {2}\ right)\ left (4.00\ times 10^ {4}\ mathrm {~m} ^ {2}\ right)\\
&=1.57\ times 10^ {10}\ mathrm {~N}.
\ end {alineado}\ nonumber\]
Discusión
Aunque esta fuerza parece grande, es pequeña en comparación con el\(1.96 \times 10^{13} \mathrm{~N}\) peso del agua en el embalse, de hecho, es solo 0.0800% del peso. Tenga en cuenta que la presión que se encuentra en la parte (a) es completamente independiente de la anchura y longitud del lago, solo depende de su profundidad promedio en la presa. Así, la fuerza depende únicamente de la profundidad media del agua y de las dimensiones de la presa, no de la extensión horizontal del embalse. En el diagrama, el grosor de la presa aumenta con la profundidad para equilibrar la fuerza creciente debido a la presión creciente.

La presión atmosférica es otro ejemplo de presión debida al peso de un fluido, en este caso debido al peso del aire por encima de una altura determinada. La presión atmosférica en la superficie de la Tierra varía un poco debido al flujo a gran escala de la atmósfera inducido por la rotación de la Tierra (esto crea “altos” y “bajos” climáticos). Sin embargo, la presión promedio al nivel del mar viene dada por la presión atmosférica estándar\(P_{\mathrm{atm}}\), medida para ser
\[1 \text { atmosphere }(\mathrm{atm})=P_{\mathrm{atm}}=1.01 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}=101 \ \mathrm{kPa} \nonumber \]
Esta relación significa que, en promedio, al nivel del mar, una columna de aire por encima\(1.00 \mathrm{~m}^{2}\) de la superficie terrestre tiene un peso de\(1.01 \times 10^{5} \mathrm{~N}\), equivalente a 1 atm. (Ver Figura\(\PageIndex{3}\).)

Ejemplo\(\PageIndex{2}\): Calculating Depth Below the Surface of Water: What Depth of Water Creates the Same Pressure as the Entire Atmosphere?
Calcular la profundidad por debajo de la superficie del agua a la que la presión debida al peso del agua es igual a 1.00 atm.
Estrategia
Comenzamos resolviendo la ecuación\(P=\rho g h\) para profundidad\(h\):
\[h=\frac{P}{\rho g}. \nonumber\]
Entonces tomamos\(P\) para ser 1.00 atm y\(\rho\) ser la densidad del agua que crea la presión.
Solución
Introducir los valores conocidos en la expresión para\(h\) da
\[h=\frac{1.01 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}}{\left(1.00 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}\right)\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)}=10.3 \mathrm{~m}. \nonumber\]
Discusión
Apenas 10.3 m de agua crea la misma presión que 120 km de aire (altura de las capas más altas de la atmósfera). Dado que el agua es casi incompresible, podemos descuidar cualquier cambio en su densidad a lo largo de esta profundidad.
¿Cuál supone que es la presión total a una profundidad de 10.3 m en una piscina? ¿La presión atmosférica en la superficie del agua afecta a la presión inferior? La respuesta es sí. Esto parece lógico, ya que tanto el peso del agua como el peso de la atmósfera deben ser sostenidos. Por lo que la presión total a una profundidad de 10.3 m es de 2 atm, la mitad del agua de arriba y la mitad del aire de arriba.
Resumen de la Sección
- La presión es el peso del fluido\(mg\) dividido por el área que lo\(A\) soporta (el área del fondo del contenedor):
\[P=\frac{m g}{A}. \nonumber\]
- La presión debida al peso de un líquido viene dada por
\[P=\rho g h, \nonumber\]
donde\(P\) esta la presión,\(\rho\) es la densidad del liquido,\(g\) es la aceleracion debida a la gravedad, y\(h\) es la altura del liquido.
Glosario
- presión debido al peso del fluido
- presión a una profundidad por debajo de una superficie de fluido debido a su peso; dada por\(P=\rho g h\)


