7.8: Ecuación de Bernoulli

Objetivos de aprendizaje

• Explique los términos en la ecuación de Bernoulli.
• Explicar cómo se relaciona la ecuación de Bernoulli con la conservación de energía.
• Explicar cómo derivar el principio de Bernoulli a partir de la ecuación de Bernoulli.
• Calcular con el principio de Bernoulli.
• Enumere algunas aplicaciones del principio de Bernoulli.

Cuando un fluido fluye hacia un canal más estrecho, su velocidad aumenta. Eso significa que su energía cinética también aumenta. ¿De dónde viene ese cambio en la energía cinética? El aumento de la energía cinética proviene del trabajo neto realizado en el fluido para empujarlo al canal y del trabajo realizado en el fluido por la fuerza gravitacional, si el fluido cambia de posición vertical. Recordemos el teorema trabajo-energía,

\[W_{\text {net }}=\frac{1}{2} m v^{2}-\frac{1}{2} m v_{0}^{2} . \nonumber \]

Hay una diferencia de presión cuando el canal se estrecha. Esta diferencia de presión da como resultado una fuerza neta sobre el fluido: recuerde que los tiempos de presión son el área igual a la fuerza. El trabajo neto realizado aumenta la energía cinética del fluido. Como resultado, la presión caerá en un fluido que se mueve rápidamente, ya sea que el fluido esté confinado o no a un tubo.

Hay una serie de ejemplos comunes de caída de presión en fluidos que se mueven rápidamente. Las cortinas de ducha tienen la desagradable costumbre de abultarse en la cabina de ducha cuando la ducha está encendida. La corriente de agua y aire a alta velocidad crea una región de menor presión dentro de la ducha y presión atmosférica estándar en el otro lado. La diferencia de presión resulta en una fuerza neta hacia adentro que empuja la cortina hacia adentro. También te habrás dado cuenta de que al pasar un camión por la carretera, tu auto tiende a desviarse hacia él. La razón es la misma: la alta velocidad del aire entre el automóvil y el camión crea una región de menor presión, y los vehículos son empujados juntos por una mayor presión en el exterior. (Ver Figura\(\PageIndex{1}\).) Este efecto se observó ya a mediados del siglo XIX, cuando se encontró que los trenes que pasaban en direcciones opuestas se inclinaban precariamente uno hacia el otro.

Figura\(\PageIndex{1}\): Vista aérea de un automóvil que pasa por un camión en una autopista. El aire que pasa entre los vehículos fluye en un canal más estrecho y debe aumentar su velocidad (\(v_{2}\)es mayor que\(v_{1}\)), provocando que la presión entre ellos baje (\(P_{\mathrm{i}}\)es menor que\(P_{\mathrm{o}}\)). Una mayor presión en el exterior empuja el auto y el camión juntos.

HACIENDO CONEXIONES: INVESTIGACIÓN PARA LLEGAR

Sostenga el borde corto de una hoja de papel paralelo a su boca con una mano a cada lado de su boca. La página debe inclinarse hacia abajo sobre tus manos. Soplar sobre la parte superior de la página. Describir lo que sucede y explicar la razón de este comportamiento.

Ecuación de Bernoulli

La relación entre presión y velocidad en fluidos se describe cuantitativamente por la ecuación de Bernoulli, que lleva el nombre de su descubridor, el científico suizo Daniel Bernoulli (1700—1782). La ecuación de Bernoulli establece que para un fluido incompresible y sin fricción, la siguiente suma es constante:

\[P+\frac{1}{2} \rho v^{2}+\rho g h=\text { constant }, \nonumber \]

donde\(P\) está la presión absoluta,\(\rho\) es la densidad del fluido,\(v\) es la velocidad del fluido,\(h\) es la altura por encima de algún punto de referencia, y\(g\) es la aceleración debida a la gravedad. Si seguimos un pequeño volumen de fluido a lo largo de su trayectoria, varias cantidades en la suma pueden cambiar, pero el total permanece constante. Deje que los subíndices 1 y 2 se refieran a dos puntos cualesquiera a lo largo de la trayectoria que sigue el bit de fluido; la ecuación de Bernoulli se convierte en

\[P_{1}+\frac{1}{2} \rho v_{1}^{2}+\rho g h_{1}=P_{2}+\frac{1}{2} \rho v_{2}^{2}+\rho g h_{2}. \nonumber \]

La ecuación de Bernoulli es una forma del principio de conservación de la energía. Tenga en cuenta que el segundo y tercer término son la energía cinética y potencial con\(m\) reemplazada por\(\rho\). De hecho, cada término de la ecuación tiene unidades de energía por unidad de volumen. Podemos probarlo para el segundo término sustituyéndolo\(\rho=m / V\) en él y reuniendo términos:

\[\frac{1}{2} \rho v^{2}=\frac{\frac{1}{2} m v^{2}}{V}=\frac{\mathrm{KE}}{V}. \nonumber \]

Así\(\frac{1}{2} \rho v^{2}\) es la energía cinética por unidad de volumen. Haciendo la misma sustitución en el tercer término en la ecuación, encontramos

\[\rho g h=\frac{m g h}{V}=\frac{\mathrm{PE}_{\mathrm{g}}}{V}, \nonumber \]

así\(\rho g h\) es la energía potencial gravitacional por unidad de volumen. Tenga en cuenta que la presión también\(P\) tiene unidades de energía por unidad de volumen. Ya que\(P=F / A\), sus unidades son\(\mathrm{N} / \mathrm{m}^{2}\). Si los multiplicamos por m/m, obtenemos\(\mathrm{N} \cdot \mathrm{m} / \mathrm{m}^{3}=\mathrm{J} / \mathrm{m}^{3}\), o energía por unidad de volumen. La ecuación de Bernoulli es, de hecho, solo una declaración conveniente de conservación de energía para un fluido incompresible en ausencia de fricción.

HACER CONEXIONES: CONSERVACIÓN

La conservación de la energía aplicada al flujo de fluidos produce la ecuación de Bernoulli. El trabajo neto realizado por la presión del fluido resulta en cambios en los fluidos\(\text { KE }\) y\(\mathrm{PE}_{\mathrm{g}}\) por unidad de volumen. Si otras formas de energía están involucradas en el flujo de fluidos, la ecuación de Bernoulli puede modificarse para tener en cuenta estas formas. Tales formas de energía incluyen la energía térmica disipada debido a la viscosidad del fluido.

La forma general de la ecuación de Bernoulli tiene tres términos en ella, y es ampliamente aplicable. Para entenderlo mejor, veremos una serie de situaciones específicas que simplifican e ilustran su uso y significado.

Ecuación de Bernoulli para fluidos estáticos

Consideremos primero la situación muy simple en la que el fluido es estático, es decir,\(v_{1}=v_{2}=0\). La ecuación de Bernoulli en ese caso es

\[P_{1}+\rho g h_{1}=P_{2}+\rho g h_{2}. \nonumber \]

Podemos simplificar aún más la ecuación tomando\(h_{2}=0\) (siempre podemos elegir alguna altura para que sea cero, tal como lo hemos hecho a menudo para otras situaciones que involucran la fuerza gravitacional, y tomar todas las demás alturas para que sean relativas a esta). En ese caso, obtenemos

\[P_{2}=P_{1}+\rho g h_{1}. \nonumber \]

Esta ecuación nos dice que, en los fluidos estáticos, la presión aumenta con la profundidad. A medida que vamos del punto 1 al punto 2 en el fluido, la profundidad aumenta en\(h_{1}\), y consecuentemente,\(P_{2}\) es mayor que\(P_{1}\) en una cantidad\(\rho g h_{1}\). En el caso muy simple,\(P_{1}\) es cero en la parte superior del fluido, y obtenemos la relación familiar\(P=\rho g h\). (Recordemos eso\(P=\rho g h\) y\(\Delta \mathrm{PE}_{\mathrm{g}}=m g h\)) La ecuación de Bernoulli incluye el hecho de que la presión debida al peso de un fluido es\(\rho g h\). Aunque introducimos la ecuación de Bernoulli para el flujo de fluidos, incluye gran parte de lo que estudiamos para los fluidos estáticos en el capítulo anterior.

Principio de Bernoulli: ecuación de Bernoulli a profundidad constante

Otra situación importante es aquella en la que el fluido se mueve pero su profundidad es constante, es decir,\(h_{1}=h_{2}\). Bajo esa condición, la ecuación de Bernoulli se convierte en

\[P_{1}+\frac{1}{2} \rho v_{1}^{2}=P_{2}+\frac{1}{2} \rho v_{2}^{2}. \nonumber \]

Las situaciones en las que el fluido fluye a una profundidad constante son tan importantes que a esta ecuación se le suele llamar principio de Bernoulli. Es la ecuación de Bernoulli para fluidos a profundidad constante. (Obsérvese nuevamente que esto se aplica a un pequeño volumen de fluido a medida que lo seguimos a lo largo de su trayectoria). Como acabamos de discutir, la presión cae a medida que aumenta la velocidad en un fluido en movimiento. Esto lo podemos ver desde el principio de Bernoulli. Por ejemplo, si\(v_{2}\) es mayor que\(v_{1}\) en la ecuación, entonces\(P_{2}\) debe ser menor que\(P_{1}\) para que la igualdad se mantenga.

Ejemplo\(\PageIndex{1}\): Calculating Pressure: Pressure Drops as a Fluid Speeds Up

En el Ejemplo 8.6.2, encontramos que la velocidad del agua en una manguera aumentó de 1.96 m/s a 25.5 m/s pasando de la manguera a la boquilla. Calcular la presión en la manguera, dado que la presión absoluta en la boquilla es\(1.01 \times 10^{5} \mathrm{~N} / \mathrm{m}^{2}\) (atmosférica, como debe ser) y asumiendo nivel, flujo sin fricción.

Estrategia

Flujo nivelado significa profundidad constante, por lo que se aplica el principio de Bernoulli. Utilizamos el subíndice 1 para los valores en la manguera y 2 para los de la boquilla. Se nos pide así que encontremos\(P_{1}\).

Solución

Resolviendo el principio de Bernoulli para\(P_{1}\) los rendimientos

\[P_{1}=P_{2}+\frac{1}{2} \rho v_{2}^{2}-\frac{1}{2} \rho v_{1}^{2}=P_{2}+\frac{1}{2} \rho\left(v_{2}^{2}-v_{1}^{2}\right). \nonumber\]

Sustituyendo valores conocidos,

\ [\ begin {aligned}
P_ {1} =& 1.01\ times 10^ {5}\ mathrm {~N}/\ mathrm {m} ^ {2}\\
&+\ frac {1} {2}\ left (10^ {3}\ mathrm {~kg}/\ mathrm {m} ^ {3}\ derecha)\ izquierda [(25.5\ mathrm {m}/\ mathrm {s}) ^ {2} - (1.96\ mathrm {~m}/\ mathrm {s}) ^ {2}\ derecha]\\
=& 4.24\ veces 10^ {5}\ mathrm { ~N}/\ mathrm {m} ^ {2}.
\ end {alineado}\ nonumber\]

Discusión

Esta presión absoluta en la manguera es mayor que en la boquilla, como se esperaba ya que v es mayor en la boquilla. La presión\(P_{2}\) en la boquilla debe ser atmosférica ya que emerge a la atmósfera sin otros cambios en las condiciones.

Aplicaciones del Principio de Bernoulli

Hay una serie de dispositivos y situaciones en las que el fluido fluye a una altura constante y, por lo tanto, se puede analizar con el principio de Bernoulli.

Entrasimiento

La gente ha puesto en práctica durante mucho tiempo el principio de Bernoulli al usar presión reducida en fluidos de alta velocidad para mover las cosas. Con una mayor presión en el exterior, el fluido de alta velocidad obliga a otros fluidos a entrar en la corriente. Este proceso se llama arrastre. Los dispositivos de arrastre han estado en uso desde la antigüedad, particularmente como bombas para elevar pequeñas alturas de agua, como en pantanos de drenaje, campos u otras áreas bajas. Algunos otros dispositivos que utilizan el concepto de arrastre se muestran en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Ejemplos de dispositivos de arrastre que utilizan mayor velocidad de fluido para crear bajas presiones, que luego arrastran un fluido a otro. (a) Un quemador Bunsen utiliza una boquilla de gas ajustable, arrastrando aire para una combustión adecuada. (b) Un atomizador utiliza una bombilla de compresión para crear un chorro de aire que arrastra gotas de perfume. Los pulverizadores de pintura y carburadores utilizan técnicas muy similares para mover sus respectivos líquidos. (c) Un aspirador común utiliza una corriente de agua de alta velocidad para crear una región de menor presión. Los aspiradores pueden ser utilizados como bombas de succión en situaciones dentales y quirúrgicas o para drenar un sótano inundado o producir una presión reducida en un vaso. d) La chimenea de un calentador de agua está diseñada para arrastrar aire a la tubería que conduce a través del techo.

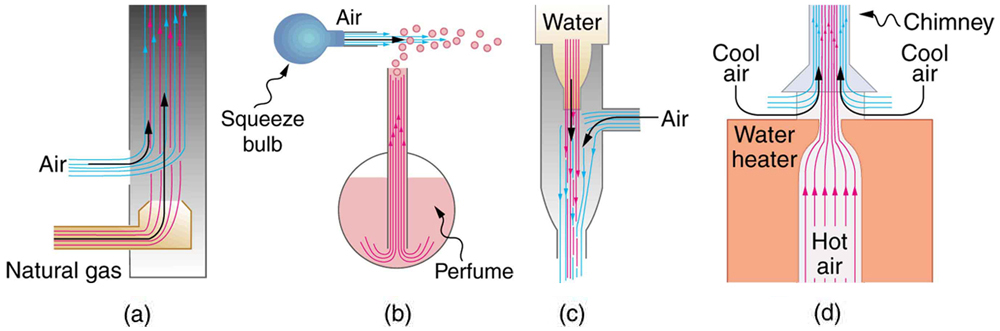
Alas y Velas

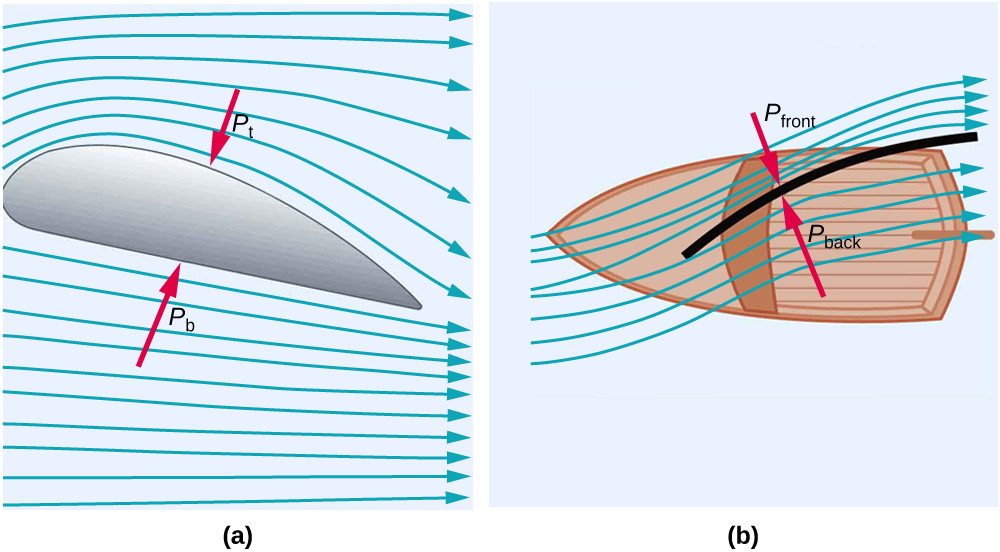
El ala del avión es un hermoso ejemplo del principio de Bernoulli en acción. La figura\(\PageIndex{3}\) (a) muestra la forma característica de un ala. El ala se inclina hacia arriba en un ángulo pequeño y la superficie superior es más larga, lo que hace que el aire fluya más rápido sobre ella. Por lo tanto, la presión en la parte superior del ala se reduce, creando una fuerza neta hacia arriba o levantamiento. (Las alas también pueden ganar sustentación empujando el aire hacia abajo, utilizando el principio de conservación del impulso. Las moléculas de aire desviadas resultan en una fuerza ascendente en el ala, la tercera ley de Newton). Las velas también tienen la forma característica de un ala. (Ver Figura\(\PageIndex{3}\) (b).) La presión en la parte delantera de la vela,\(P_{\text {front }}\), es menor que la presión sobre la parte posterior de la vela,\(P_{\text {back }}\). Esto da como resultado una fuerza hacia adelante e incluso te permite navegar hacia el viento.

HACIENDO CONEXIONES: INVESTIGACIÓN PARA LLEGAR

Para una buena ilustración del principio de Bernoulli, haz dos tiras de papel, cada una de aproximadamente 15 cm de largo y 4 cm de ancho. Sostén el extremo pequeño de una tira hasta tus labios y deja que se cuelgue sobre tu dedo. Soplar sobre el papel. ¿Qué pasa? Ahora sujeta dos tiras de papel hasta tus labios, separadas por tus dedos. Soplar entre las tiras. ¿Qué pasa?

Medición de velocidad

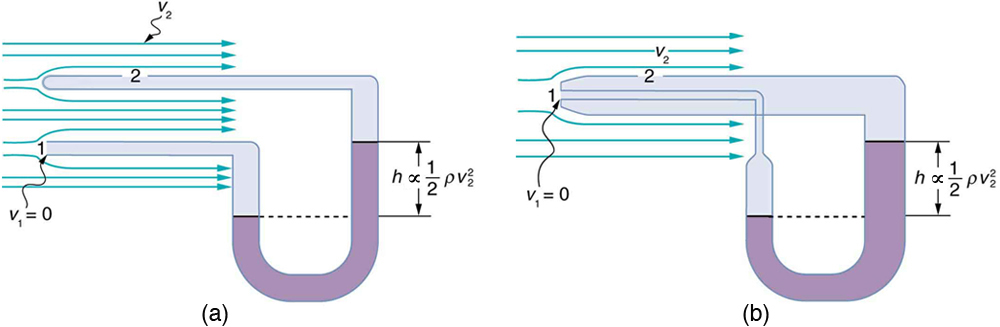
La figura\(\PageIndex{4}\) muestra dos dispositivos que miden la velocidad del fluido con base en el principio de Bernoulli. El manómetro de la Figura\(\PageIndex{4}\) (a) está conectado a dos tubos que son lo suficientemente pequeños como para no perturbar apreciablemente el flujo. El tubo que mira hacia el fluido que se aproxima crea un punto muerto que tiene velocidad cero (\(v_{1}=0\)) frente a él, mientras que el fluido que pasa por el otro tubo tiene velocidad\(v_{2}\). Esto significa que el principio de Bernoulli, tal como\(P_{1}+\frac{1}{2} \rho v_{1}^{2}=P_{2}+\frac{1}{2} \rho v_{2}^{2}\) se afirma en

\[P_{1}=P_{2}+\frac{1}{2} \rho v_{2}^{2}. \nonumber \]

Figura\(\PageIndex{3}\): (a) El principio de Bernoulli ayuda a explicar la elevación generada por un ala. b) Las velas utilizan la misma técnica para generar parte de su empuje.

Así la presión\(P_{2}\) sobre la segunda abertura se reduce en\(\frac{1}{2} \rho v_{2}^{2}\), y así el fluido en el manómetro se eleva\(h\) en el lado conectado a la segunda abertura, donde

\[h \propto \frac{1}{2} \rho v_{2}^{2}. \nonumber \]

(Recordemos que el símbolo\(\propto\) significa “proporcional a.”) Resolviendo para\(v_{2}\), vemos que

\[v_{2} \propto \sqrt{h}. \nonumber \]

La Figura\(\PageIndex{4}\) (b) muestra una versión de este dispositivo que es de uso común para medir diversas velocidades de fluido; dichos dispositivos se utilizan frecuentemente como indicadores de velocidad del aire en aeronaves.

Figura\(\PageIndex{4}\): Medición de la velocidad del fluido basada en el principio de Bernoulli. (a) Un manómetro está conectado a dos tubos que están muy cerca entre sí y lo suficientemente pequeños como para no perturbar el flujo. El tubo 1 está abierto en el extremo orientado hacia el flujo. Allí se crea un punto muerto que tiene velocidad cero. El tubo 2 tiene una abertura lateral, por lo que el fluido tiene una velocidad\(v\) a través de la abertura; así, la presión ahí baja. La diferencia de presión en el manómetro es\(\frac{1}{2} \rho v_{2}^{2}\), y así h es proporcional a\(\frac{1}{2} \rho v_{2}^{2}\). (b) Este tipo de dispositivo de medición de velocidad es un tubo Prandtl, también conocido como tubo pitot.

Resumen

• La ecuación de Bernoulli establece que la suma en cada lado de la siguiente ecuación es constante, o la misma en dos puntos cualesquiera en un fluido sin fricción incompresible:

  \[P_{1}+\frac{1}{2} \rho v_{1}^{2}+\rho g h_{1}=P_{2}+\frac{1}{2} \rho v_{2}^{2}+\rho g h_{2}. \nonumber\]

• El principio de Bernoulli es la ecuación de Bernoulli aplicada a situaciones en las que la profundidad es constante. Los términos que implican profundidad (o altura h) restan, cediendo

  \[P_{1}+\frac{1}{2} \rho v_{1}^{2}=P_{2}+\frac{1}{2} \rho v_{2}^{2}. \nonumber\]

• El principio de Bernoulli tiene muchas aplicaciones, incluyendo arrastre, alas y velas, y medición de velocidad.

Glosario

Ecuación de Bernoulli

la ecuación resultante de aplicar conservación de energía a un fluido incompresible sin fricción: P + 1/2 pv ² + pgh = constante, a través del fluido

Principio de Bernoulli

Ecuación de Bernoulli aplicada a profundidad constante: P ₁ + 1/2 pv ₁ ² = P ₂ + 1/2 pv ₂ ²