3.3: Matrices

A menudo tendremos que lidiar con colecciones de varios números, lo que requiere organizarlos en estructuras de datos. Una de las estructuras de datos que usaremos con mayor frecuencia es la matriz, que es una secuencia lineal de números de tamaño fijo. Ya hemos discutido el uso básico de las matrices Scipy en el artículo anterior.

La disposición de memoria de una matriz se muestra esquemáticamente en la Fig. \(\PageIndex{1}\). Consta de dos regiones separadas de memoria:

Figura\(\PageIndex{1}\): Esquema de cómo se presenta una matriz en la memoria. El bloque de contabilidad (cuadro superior izquierdo) registra el tamaño de la matriz, la dirección de los bloques de almacenamiento (indicada por una flecha), etc. Los bloques de almacenamiento (cajas inferiores a la derecha) contienen el contenido de la matriz, en orden secuencial.

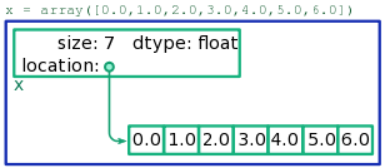
1. Una región, que llamamos el bloque de contabilidad, almacena información resumida sobre la matriz, incluyendo (i) el número total de elementos, (ii) la dirección de memoria donde se almacena el contenido de la matriz (específicamente, la dirección del elemento 0) y (iii) el tipo de números almacenados en la matriz. Los dos primeros datos se registran en forma de enteros, mientras que la última pieza se graba en algún otro formato del que no necesitamos preocuparnos (es administrado por Python).
2. La segunda región, a la que llamamos el bloque de datos, almacena los contenidos reales de la matriz, dispuestos secuencialmente. Por ejemplo, para una matriz que contenga siete enteros de 64 bits, este bloque consistirá en\(7\times 64=448\) bits de memoria, almacenando los enteros uno tras otro.

El bloque de contabilidad y el bloque de datos no necesariamente se mantienen uno al lado del otro en la memoria. Cuando un fragmento de código Python actúa sobre una matriz x, la información en el bloque de contabilidad de la matriz se usa para ubicar el bloque de datos y luego acceder/alterar sus datos según sea necesario.

3.3.1 Operaciones básicas de arreglos

Echemos un vistazo detallado a lo que sucede cuando leemos o escribimos un elemento individual de una matriz, digamos x [2]: el tercer elemento (índice\(2\)) almacenado en la matriz x.

Por el nombre de la matriz, x, Python conoce la dirección del bloque de contabilidad relevante (esto es manejado internamente por Python y lleva un tiempo insignificante). El bloque de contabilidad registra la dirección del elemento\(0\), es decir, el inicio del bloque de datos. Debido a que queremos índice\(2\) de la matriz, el procesador salta a la dirección de memoria que es\(2\) bloques más allá de la dirección grabada. Dado que el bloque de datos se presenta secuencialmente, esa es precisamente la dirección donde se almacena el número x [2]. Este número ahora se puede leer o sobrescribir, según lo desee el código Python.

Bajo este esquema, la lectura/escritura de elementos individuales de la matriz es independiente del tamaño de la matriz. Acceder a un elemento en una\(1\) matriz de tamaño toma el mismo tiempo que acceder a un elemento en una\(100000\) matriz de tamaño. Esto se debe a que la memoria es de acceso aleatorio: el procesador puede saltar a cualquier dirección en la memoria una vez que le digas a dónde ir. El diseño de memoria de una matriz está diseñado para que siempre se pueda calcular la dirección relevante en un solo paso.

Describimos la velocidad de esta operación usando notación Big-O. Si\(N\) es el tamaño de la matriz, se dice que la lectura/escritura de elementos individuales de la matriz toma\(O(1)\) tiempo, o “orden-\(1\) tiempo” (es decir, independiente de\(N\)). Por el contrario, una declaración como

x.fill(3.3)

toma\(O(N)\) tiempo, es decir, tiempo proporcional al tamaño de la matriz\(N\). Eso es porque el método fill asigna valores a cada uno de los\(N\) elementos de la matriz. De igual manera, el comunicado

x += 1.0

lleva\(O(N)\) tiempo. Esta operación += agrega 1.0 a cada uno de los elementos de la matriz, lo que requiere operaciones\(N\) aritméticas.

3.3.2 Tipo de datos de matriz

Hemos observado que el bloque de contabilidad de cada matriz registra el tipo de número, o tipo de datos, guardado en los bloques de almacenamiento. Por lo tanto, cada matriz individual es capaz de almacenar solo un tipo de número. Cuando se crea una matriz con la función array, Scipy infiere el tipo de datos en función del contenido de la matriz especificada. Por ejemplo, si la entrada contiene solo enteros, se crea una matriz de enteros; si luego intenta almacenar un número de punto flotante, se redondeará a un entero:

>>> a = array([1,2,3,4])
>>> a[1] = 3.14159
>>> a
array([1, 3, 3, 4])

En la situación anterior, si nuestra intención era crear una matriz de números de punto flotante, eso se puede hacer dando a la función array una entrada que contenga al menos un número de punto flotante. Por ejemplo,

>>> a = array([1,2,3,4.])
>>> a[1] = 3.14159
>>> a
array([ 1.     ,  3.14159,  3.     ,  4.     ])

Alternativamente, la función array acepta un parámetro llamado dtype, que se puede usar para especificar el tipo de datos directamente:

>>> a = array([1,2,3,4], dtype=float)
>>> a[1] = 3.14159
>>> a
array([ 1.     ,  3.14159,  3.     ,  4.     ])

El parámetro dtype acepta varios valores posibles, pero la mayoría de las veces elegirás uno de estos tres:

• flotar
• complejo
• entero

Las funciones comunes para crear nuevas matrices, ceros unos y linspace, crean matrices con el tipo de datos flotantes por defecto. También aceptan parámetros dtype, en caso de que desee un tipo de datos diferente. Por ejemplo:

>>> a = zeros(4, dtype=complex)
>>> a[1] = 2.5+1j
>>> a
array([ 0.0+0.j,  2.5+1.j,  0.0+0.j,  0.0+0.j])

3.3.3 Vectorización

Ya hemos discutido previamente el código x += 1.0, que agrega 1.0 a cada elemento de la matriz x. Tiene tiempo de ejecución\(O(N)\), donde\(N\) está la longitud de la matriz. También podríamos haber hecho lo mismo haciendo un bucle sobre la matriz, de la siguiente manera:

for n in range(len(x)):
    x[n] += 1.0

Esto, también, tiene\(O(N)\) tiempo de ejecución. Pero no es una buena manera de hacer el trabajo, por dos razones. En primer lugar, obviamente es mucho más engorroso escribir. En segundo lugar, y lo que es más importante, es mucho más ineficiente, porque implica más operaciones de Python de “alto nivel”. Para ejecutar este código, Python tiene que crear una variable de índice n, incrementar esa variable de índice\(N\) veces, e incrementar x [n] para cada valor separado de n.

Por el contrario, cuando escribes x += 1.0, Python usa código de “bajo nivel” para incrementar cada elemento de la matriz, lo que no requiere introducir y administrar ningún objeto Python de “alto nivel”. La práctica de usar operaciones de matriz, en lugar de realizar bucles explícitos sobre una matriz, se llama vectorización. Siempre debe esforzarse por vectorizar su código; generalmente es una buena práctica de programación y conduce a ganancias de rendimiento extremas para tamaños de matriz grandes.

La vectorización no cambia el escalado en tiempo de ejecución de la operación. El código vectorizado x += 1.0, y el bucle explícito, ambos se ejecutan en el\(O(N)\) tiempo. Lo que cambia es el coeficiente del escalado: el tiempo de ejecución tiene la forma\(T\), y el valor del coeficiente\(a\) es mucho menor para el código vectorizado.

Aquí hay otro ejemplo de vectorización. Supongamos que tenemos una variable y cuyo valor es un número, y una matriz x que contiene una colección de números; queremos encontrar el elemento de x más cercano a y. Aquí hay código no vectorizado para hacer esto:

idx, distance = 0, abs(x[0] - y)
for n in range(1, len(x)):
    new_dist = abs(x[n] - y)
    if new_dist < distance:
        idx, distance = n, new_dist

z = x[idx]

El enfoque vectorizado simplemente haría uso de la función argmin:

idx = argmin(abs(x - y))
z = x[idx]

La forma en que esto funciona es crear una nueva matriz, cuyos valores son las distancias entre cada elemento de x y el número objetivo y; luego, argmin busca el índice de matriz correspondiente al elemento más pequeño (que también es el índice del elemento de x más cercano a y). Podríamos escribir este código de forma aún más compacta como

z = x[argmin(abs(x - y))]

3.3.4 Rebanado de Matrices

Hemos enfatizado que una matriz se presenta en la memoria en dos piezas: un bloque de contabilidad y una secuencia de bloques de almacenamiento que contienen los elementos de la matriz. A veces, es posible que dos arreglos compartan bloques de almacenamiento. Por ejemplo, esto sucede cuando realiza el corte de matrices:

>>> x = array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0])
>>> y = x[2:5]
>>> y
array([ 2.,  3.,  4.])

La instrucción y = x [2:5] crea una matriz llamada y, que contiene un subconjunto de los elementos de x (es decir, los elementos en los índices\(2\)\(3\), y\(4\)). Sin embargo, Python no logra esto copiando los elementos afectados de x en una nueva matriz con nuevos bloques de almacenamiento. En su lugar, crea un nuevo bloque de contabilidad para y, y lo apunta hacia los bloques de almacenamiento existentes de x:

Figura\(\PageIndex{2}\): Dos arreglos, x e y, que comparten los mismos bloques de almacenamiento.

Debido a que los bloques de almacenamiento se comparten entre dos matrices, si cambiamos un elemento en x, eso cambia efectivamente el contenido de y también:

>>> x[3] = 9.
>>> y
array([ 2.,  9.,  4.])

(La situación es similar si especifica un “paso” durante el corte, como y = x [2:5:2]. Lo que sucede en ese caso es que el bloque de datos realiza un seguimiento del tamaño del paso, y Python puede usar esto para averiguar exactamente qué dirección saltar para acceder a cualquier elemento dado).

Lo bueno de este método de compartir bloques de almacenamiento es que el corte es una\(O(1)\) operación, independiente del tamaño de la matriz. Python no necesita hacer ninguna copia en los elementos almacenados; simplemente necesita crear un nuevo bloque de contabilidad. Por lo tanto, el rebanado es una operación muy “barata” y eficiente.

La desventaja es que puede llevar a extraños bichos. Por ejemplo, este es un error común:

>>> x = y = linspace(0, 1, 100)

La sentencia anterior crea dos matrices, x e y, apuntando a los mismos bloques de almacenamiento. ¡Esto casi definitivamente no es lo que pretendemos! La forma correcta es escribir dos instrucciones de inicialización de matriz separadas.

Siempre que pretendas copiar una matriz y cambiar su contenido libremente sin afectar a la matriz original, debes recordar usar la función copy:

>>> x = array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0])
>>> y = copy(x[2:5])
>>> x[3] = 9.
>>> y
array([ 2.,  3.,  4.])

En el ejemplo anterior, la sentencia y = copy (x [2:5]) copia explícitamente los bloques de almacenamiento de x. Por lo tanto, cuando cambiamos el contenido de x, los contenidos de y no se ven afectados.

¡No llames a copy demasiado liberalmente! Es una\(O(N)\) operación, por lo que la copia innecesaria perjudica el rendimiento. En particular, las operaciones aritméticas básicas no afectan el contenido de las matrices, por lo que siempre es seguro escribir

>>> y = x + 4

en lugar de y = copy (x) + 4.