9.1: Regla de punto medio
- Page ID
- 125279
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
El método de integración numérica más simple se llama regla de punto medio. Considere una integral 1D definida
\[\mathcal{I} = \int_a^b f(x) \, dx.\]
Dividamos el rango\(a \le x \le b\) en un conjunto de\(N\) segmentos de igual ancho, como se muestra en la Fig. \(\PageIndex{1}\)para el caso de\(N=5\). Los puntos medios de estos segmentos son un conjunto de puntos\(N\) discretos\(\{x_0, \dots x_{N-1}\}\), donde
\[x_n = a + \left(n + \frac{1}{2}\right)\,\Delta x ,\quad \Delta x \equiv \frac{b-a}{N}.\]
Luego estimamos la integral como
\[\mathcal{I}^{\mathrm{(mp)}} = \Delta x \; \sum_{n=0}^{N-1} f(x_n) \;\;\;\overset{N\rightarrow\infty}{\longrightarrow} \;\;\; \mathcal{I}.\]
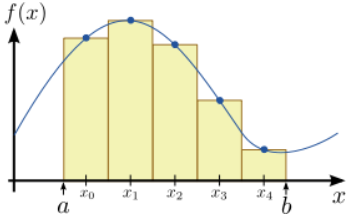
El principio detrás de esta fórmula es muy sencillo de entender. Como se muestra en la Fig. \(\PageIndex{1}\),\(I_{N}\) representa el área encerrada por una secuencia de rectángulos, donde la altura de cada rectángulo es igual al valor de\(f(x)\) en su punto medio. Como\(N \rightarrow \infty\), el espaciado entre rectángulos va a cero; por lo tanto, el área total encerrada por los rectángulos se vuelve igual al área bajo la curva de\(f(x)\).
9.1.1 Error numérico para la regla de punto medio
Estimemos el error numérico resultante de esta aproximación. Para ello, considere uno de los segmentos individuales, el cual se centra en\(x_n\) con longitud\(\Delta x = (b-a)/N\). Definamos la integral sobre este segmento como
\[\Delta \mathcal{I}_n \equiv \int_{x_n - \Delta x/2}^{x_n + \Delta x/2} f(x) dx.\]
Ahora, considere la expansión Taylor de\(f(x)\) en las inmediaciones de\(x_{n}\):
\[f(x) = f(x_n) + f'(x_n) (x-x_n) + \frac{f''(x_n)}{2} (x-x_n)^2 + \frac{f'''(x_n)}{6} (x-x_n)^3 + \cdots \]
Si integramos ambos lados de esta ecuación sobre el segmento, el resultado es
\[\begin{align}\Delta\mathcal{I}_n \; = \; f(x_n) \Delta x \;\,&+\; f'(x_n) \int_{x_n - \Delta x/2}^{x_n + \Delta x/2} (x-x_n) dx\\ &+\; \frac{f''(x_n)}{2} \int_{x_n - \Delta x/2}^{x_n + \Delta x/2} (x-x_n)^2 dx\\ &+\; \cdots\end{align}\]
En el lado derecho, cualquier otro término implica un integrando que es extraño alrededor\(x_{n}\). Dichos términos se integran a cero. De los términos restantes, encontramos las siguientes series para la integral de\(f(x)\) sobre el segmento:
\[\Delta\mathcal{I}_n \; = \; f(x_n) \Delta x \;+\; \frac{f''(x_n) \Delta x^3}{24} + O(\Delta x^5).\]
Por comparación, la estimación proporcionada por la regla del punto medio es simplemente
\[\Delta \mathcal{I}^{\mathrm{mp}}_n = f(x_n) \Delta x\]
Este es simplemente el primer término de la serie exacta. Los términos restantes constituyen el error numérico en la integración de reglas de punto medio, sobre este segmento. Denotamos este error como
\[\mathcal{E}_n = \left|\Delta \mathcal{I}_n - \Delta \mathcal{I}_n^{\mathrm{mp}}\right| \;\sim\; \frac{|f''(x_n)|}{24} \Delta x^3 \;\sim\; O\left(\frac{1}{N^3}\right).\]
El último paso se produce porque, por nuestra definición,\(\Delta x \sim O(1/N)\).
Ahora, considere la integral en todo el rango de integración, que consiste en\(N\) dichos segmentos. En general, no hay garantía de que los errores numéricos de cada segmento se cancelen, por lo que el error total debe ser\(N\) veces el error de cada segmento. De ahí que, para la regla del punto medio,
\[\mathcal{E}_{\mathrm{total}} \sim O\left(\frac{1}{N^2}\right).\]


