9.2: Regla de Trapecio

La regla de trapecio es una extensión simple de la regla de integración de punto medio. En lugar de calcular el área de una secuencia de rectángulos, calculamos el área de una secuencia de trapecios, como se muestra en la Fig. \(\PageIndex{1}\). Como antes, dividimos la región de integración en segmentos\(N\) iguales; sin embargo, ahora consideramos los puntos finales de estos segmentos, en lugar de sus puntos medios. Se trata de un conjunto de\(N+1\) posiciones\(\{x_0, \dots x_{N}\}\), de tal manera que

\[x_n = a + n\, \Delta x ,\quad \Delta x \equiv \frac{b-a}{N}.\]

Figura\(\PageIndex{1}\): Computar una integral definida usando la regla del trapecio.

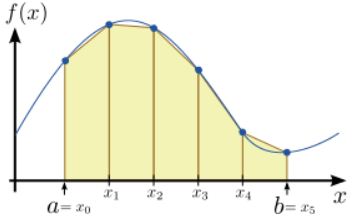
Tenga en cuenta que\(a = x_0\) y\(b=x_{N}\). Mediante el uso de la fórmula familiar para el área de cada trapecio, podemos aproximar la integral como

\[\begin{align}\mathcal{I}^{\mathrm{trapz}} &= \sum_{n=0}^{N-1} \Delta x \left(\frac{f(x_n) + f(x_{n+1})}{2}\right) \\ &= \Delta x \left[\left(\frac{f(x_0) + f(x_1)}{2}\right)+ \left(\frac{f(x_1) + f(x_2)}{2}\right) + \cdots + \left(\frac{f(x_{N-1}) + f(x_{N})}{2}\right)\right] \\ &= \Delta x \left[\frac{f(x_0)}{2} + \left(\sum_{n=1}^{N-1} f(x_n)\right) + \frac{f(x_{N})}{2}\right].\end{align}\]

9.2.1 Implementación Python de la regla de trapecio

En Scipy, la regla del trapecio es implementada por la función trapz. Por lo general, toma dos argumentos de matriz, y y x; luego la función llamada trapz (y, x) devuelve la estimación de regla de trapecio para\(\int y \;dx\), usando los elementos de x como los puntos de discretización, y los elementos de y como los valores del integrando en esos puntos.

Nota

Ma tlab nota de compatibilidad: ¡Ten cuidado con el orden de las entradas! Para la función Scipy, es trapz (y, x). Para la función Matlab del mismo nombre, las entradas se suministran en el orden opuesto, como trapz (x, y).

Tenga en cuenta que los puntos de discretización en x no necesitan estar igualmente espaciados. Alternativamente, puede llamar a la función como trapz (y, dx=s); esto realiza la integración numérica asumiendo puntos de discretización equidistantes, con espaciado s.

Aquí hay un ejemplo del uso de trapz para evaluar la integral\(\int_0^\infty \exp(-x^2) dx = 1\):

>>> from scipy import *
>>> x = linspace(0,10,25)
>>> y = exp(-x)
>>> t = trapz(y,x)
>>> print(t)
1.01437984777

9.2.2 Error numérico para la regla del trapecio

A partir de una comparación visual de la Fig. 9.1.1 (para la regla del punto medio) y la Fig. \(\PageIndex{1}\)(para la regla del trapecio), podríamos estar tentados a concluir que la regla del trapecio debería ser más precisa. Antes de saltar a esa conclusión, sin embargo, hagamos el cálculo real del error numérico. Esto es similar a nuestro cálculo anterior del error numérico de la regla del punto medio. Para la regla del trapecio, sin embargo, es conveniente considerar un par de segmentos adyacentes, que se encuentran entre los tres puntos de discretización\(\left\{x_{n-1}, x_n, x_{n+1}\right\}\).

Como antes, realizamos una expansión Taylor de\(f(x)\) en las inmediaciones de\(x_{n}\):

\[f(x) = f(x_n) + f'(x_n) (x-x_n) + \frac{f''(x_n)}{2} (x-x_n)^2 + \frac{f'''(x_n)}{6} (x-x_n)^3 + \cdots \]

Si integramos\(f(x)\) de\(x_{n-1}\) a\(x_{n+1}\), el resultado es

\[\begin{align} \mathcal{I}_n & \equiv \int_{x_n - \Delta x}^{x_n + \Delta x} f(x) dx \\ &= \; 2 f(x_n) \Delta x \;\;+\; f'(x_n) \int_{x_n - \Delta x}^{x_n + \Delta x} (x-x_n) dx \; +\; \frac{f''(x_n)}{2} \int_{x_n - \Delta x}^{x_n + \Delta x} (x-x_n)^2 dx \; +\; \cdots \end{align}\]

Como antes, cualquier otro término del lado derecho se integra a cero. Nos quedamos con

\[\mathcal{I}_n \; = \; 2 f(x_n) \Delta x \;+\; \frac{f''(x_n)}{3} \Delta x^3 + O(\Delta x^5) \;+\; \cdots \]

Esto tiene que compararse con la estimación producida por la regla del trapecio, que es

\[\mathcal{I}_n^{\mathrm{(trapz)}} = \Delta x \left[ \frac{f(x_{n-1})}{2} + f(x_n) + \frac{f(x_{n+1})}{2}\right].\]

Si Taylor expandimos el primer y último término de la expresión anterior alrededor\(x_{n}\), el resultado es:

\[\begin{align} \mathcal{I}_n^{\mathrm{(trapz)}} & = \frac{\Delta x}{2} \left[f(x_n) - f'(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^2 - \frac{f'''(x_n)}{6} \Delta x^3 + \frac{f''''(x_n)}{24} \Delta x^4 + O(\Delta x^4)\right] \\ &\quad + \;\;\Delta x \; f(x_n) \\ &\quad + \frac{\Delta x}{2} \left[f(x_n) + f'(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^2 + \frac{f'''(x_n)}{6} \Delta x^3 + \frac{f''''(x_n)}{24} \Delta x^4 + O(\Delta x^4)\right] \\ & = 2 f(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^3 + O(\Delta x^5). \end{align}\]

Por lo tanto, el error numérico para integrar sobre este par de segmentos es

\[\mathcal{E}_n \;\equiv\; \left|\mathcal{I}_n - \mathcal{I}_n^{\mathrm{trapz}}\right| \;=\; \frac{|f''(x_n)|}{6} \Delta x^3 \;\sim\; O\left(\frac{1}{N^3}\right).\]

Y el error numérico total va como

\[\mathcal{E}_{\mathrm{total}} \sim O\left(\frac{1}{N^2}\right),\]

¡que es el mismo escalado que la regla del punto medio! A pesar de nuestras expectativas, la regla del trapecio no es en realidad una mejora sobre la regla del punto medio, en lo que respecta a la precisión numérica.